Question Number 114773 by soumyasaha last updated on 21/Sep/20
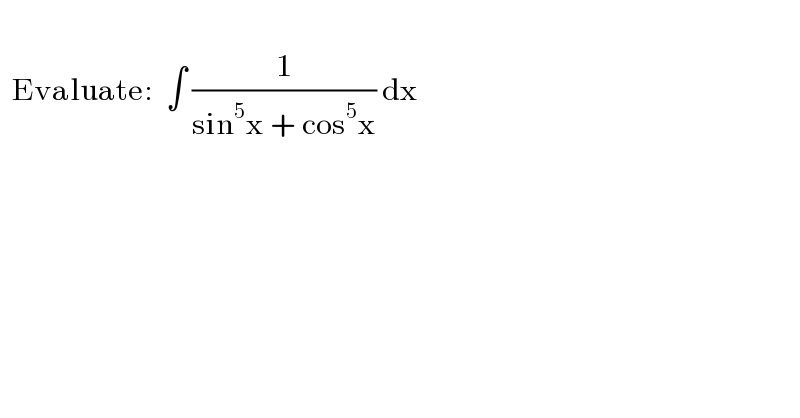
$$\: \\ $$$$\:\:\mathrm{Evaluate}:\:\:\int\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{5}} \mathrm{x}\:+\:\mathrm{cos}^{\mathrm{5}} \mathrm{x}}\:\mathrm{dx} \\ $$
Answered by MJS_new last updated on 21/Sep/20
![∫(dx/(sin^5 x +cos^5 x))= [t=x+(π/4) → dx=dt] =∫(dt/(sin^5 (t+(π/4)) −cos^5 (t+(π/4))))= [use trigonometric transformation formulas] =2(√2)∫(dt/((5−sin^4 t)sin t))= =((2(√2))/5)(∫(dt/(sin t))+∫((sin t)/( (√5)−2sin^2 t))dt−∫((sin t)/( (√5)+2sin^2 t))dt) and these are easy to solve](https://www.tinkutara.com/question/Q114789.png)
$$\int\frac{{dx}}{\mathrm{sin}^{\mathrm{5}} \:{x}\:+\mathrm{cos}^{\mathrm{5}} \:{x}}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\frac{\pi}{\mathrm{4}}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\int\frac{{dt}}{\mathrm{sin}^{\mathrm{5}} \:\left({t}+\frac{\pi}{\mathrm{4}}\right)\:−\mathrm{cos}^{\mathrm{5}} \:\left({t}+\frac{\pi}{\mathrm{4}}\right)}= \\ $$$$\:\:\:\:\:\left[\mathrm{use}\:\mathrm{trigonometric}\:\mathrm{transformation}\:\:\mathrm{formulas}\right] \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\int\frac{{dt}}{\left(\mathrm{5}−\mathrm{sin}^{\mathrm{4}} \:{t}\right)\mathrm{sin}\:{t}}= \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{5}}\left(\int\frac{{dt}}{\mathrm{sin}\:{t}}+\int\frac{\mathrm{sin}\:{t}}{\:\sqrt{\mathrm{5}}−\mathrm{2sin}^{\mathrm{2}} \:{t}}{dt}−\int\frac{\mathrm{sin}\:{t}}{\:\sqrt{\mathrm{5}}+\mathrm{2sin}^{\mathrm{2}} \:{t}}{dt}\right) \\ $$$$\mathrm{and}\:\mathrm{these}\:\mathrm{are}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
Commented by soumyasaha last updated on 21/Sep/20
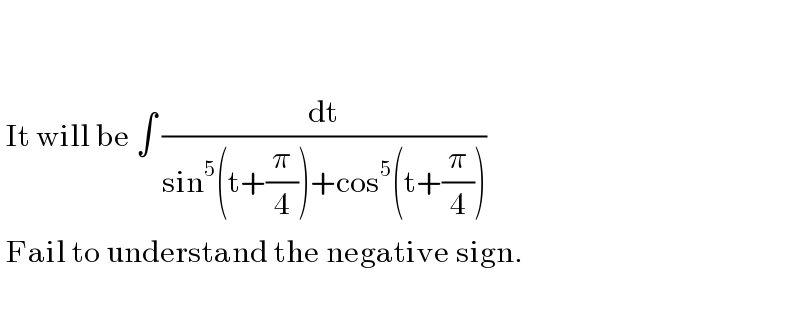
$$ \\ $$$$ \\ $$$$\:\mathrm{It}\:\mathrm{will}\:\mathrm{be}\:\int\:\frac{\mathrm{dt}}{\mathrm{sin}^{\mathrm{5}} \left(\mathrm{t}+\frac{\pi}{\mathrm{4}}\right)+\mathrm{cos}^{\mathrm{5}} \left(\mathrm{t}+\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\:\mathrm{Fail}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{negative}\:\mathrm{sign}. \\ $$$$ \\ $$
Commented by soumyasaha last updated on 21/Sep/20

$$\:\:\mathrm{how}\:+\mathrm{cos}^{\mathrm{5}} \mathrm{x}\:=\:−\mathrm{cos}^{\mathrm{5}} \left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)\:? \\ $$
Commented by soumyasaha last updated on 21/Sep/20

$$\mathrm{Kindly}\:\mathrm{show}\:\mathrm{the}\:\mathrm{inbetween}\:\mathrm{steps}… \\ $$
Commented by MJS_new last updated on 21/Sep/20
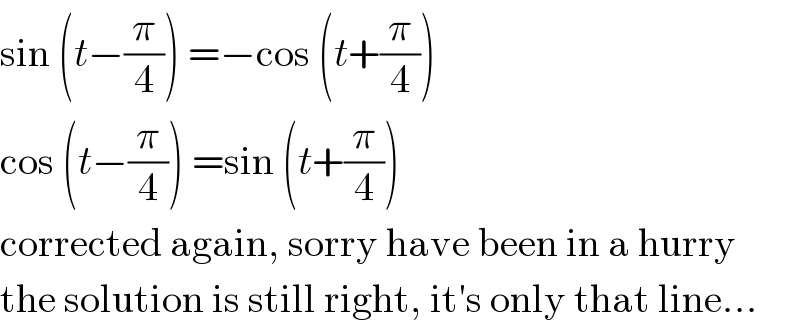
$$\mathrm{sin}\:\left({t}−\frac{\pi}{\mathrm{4}}\right)\:=−\mathrm{cos}\:\left({t}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{cos}\:\left({t}−\frac{\pi}{\mathrm{4}}\right)\:=\mathrm{sin}\:\left({t}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{corrected}\:\mathrm{again},\:\mathrm{sorry}\:\mathrm{have}\:\mathrm{been}\:\mathrm{in}\:\mathrm{a}\:\mathrm{hurry} \\ $$$$\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{still}\:\mathrm{right},\:\mathrm{it}'\mathrm{s}\:\mathrm{only}\:\mathrm{that}\:\mathrm{line}… \\ $$
Commented by MJS_new last updated on 21/Sep/20
![−cos (t+(π/4)) =((√2)/2)(sin t −cos t) sin (t+(π/4)) =((√2)/2)(sin t +cos t) (((√2)/2)(s−c))^5 +(((√2)/2)(s+c))^5 = =((√2)/4)s(s^4 +10s^2 c^2 +5c^4 )= [c=(√(1−s^2 ))] =((√2)/4)s(5−4s^4 )](https://www.tinkutara.com/question/Q114867.png)
$$−\mathrm{cos}\:\left({t}+\frac{\pi}{\mathrm{4}}\right)\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{sin}\:{t}\:−\mathrm{cos}\:{t}\right) \\ $$$$\mathrm{sin}\:\left({t}+\frac{\pi}{\mathrm{4}}\right)\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{sin}\:{t}\:+\mathrm{cos}\:{t}\right) \\ $$$$\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left({s}−{c}\right)\right)^{\mathrm{5}} +\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left({s}+{c}\right)\right)^{\mathrm{5}} = \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}{s}\left({s}^{\mathrm{4}} +\mathrm{10}{s}^{\mathrm{2}} {c}^{\mathrm{2}} +\mathrm{5}{c}^{\mathrm{4}} \right)= \\ $$$$\:\:\:\:\:\left[{c}=\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}{s}\left(\mathrm{5}−\mathrm{4}{s}^{\mathrm{4}} \right) \\ $$
Commented by soumyasaha last updated on 21/Sep/20

$$\mathrm{Thanks}\:\mathrm{Sir}.. \\ $$
