Question Number 180520 by cortano1 last updated on 13/Nov/22

$$\:\:\:\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{triangles}\: \\ $$$$\:\:\:\mathrm{that}\:\mathrm{can}\:\mathrm{be}\:\mathrm{formed}\:\mathrm{by}\:\mathrm{5}\:\mathrm{points}\: \\ $$$$\:\:\:\mathrm{in}\:\mathrm{a}\:\mathrm{line}\:\mathrm{and}\:\mathrm{3}\:\mathrm{points}\:\mathrm{on}\:\mathrm{a}\:\mathrm{parralel}\:\mathrm{line} \\ $$$$\:\:\:\mathrm{is}\:\_\_\_\: \\ $$
Answered by nikif99 last updated on 13/Nov/22
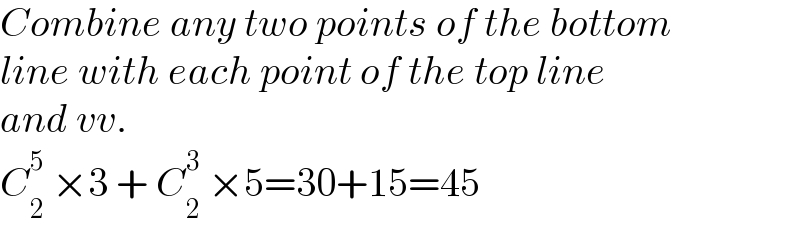
$${Combine}\:{any}\:{two}\:{points}\:{of}\:{the}\:{bottom} \\ $$$${line}\:{with}\:{each}\:{point}\:{of}\:{the}\:{top}\:{line}\: \\ $$$${and}\:{vv}. \\ $$$${C}_{\mathrm{2}} ^{\mathrm{5}} \:×\mathrm{3}\:+\:{C}_{\mathrm{2}} ^{\mathrm{3}} \:×\mathrm{5}=\mathrm{30}+\mathrm{15}=\mathrm{45} \\ $$
Commented by cortano1 last updated on 13/Nov/22
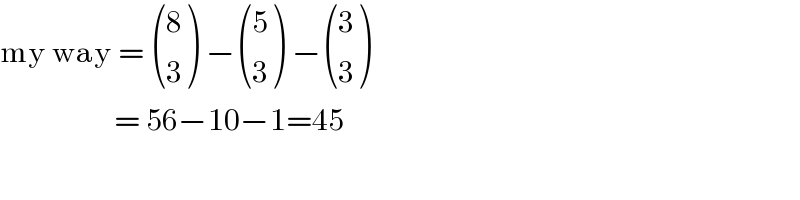
$$\mathrm{my}\:\mathrm{way}\:=\:\begin{pmatrix}{\mathrm{8}}\\{\mathrm{3}}\end{pmatrix}\:−\begin{pmatrix}{\mathrm{5}}\\{\mathrm{3}}\end{pmatrix}\:−\begin{pmatrix}{\mathrm{3}}\\{\mathrm{3}}\end{pmatrix}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{56}−\mathrm{10}−\mathrm{1}=\mathrm{45} \\ $$
Answered by Acem last updated on 13/Nov/22
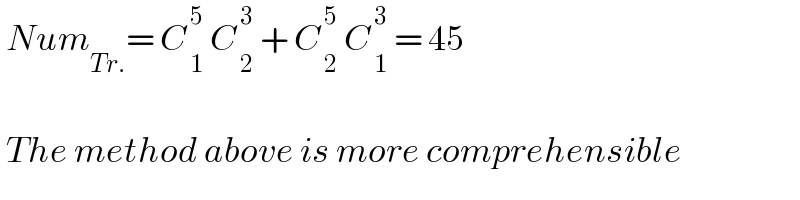
$$\:{Num}_{{Tr}.} =\:{C}_{\:\mathrm{1}} ^{\:\mathrm{5}} \:{C}_{\:\mathrm{2}} ^{\:\mathrm{3}} \:+\:{C}_{\:\mathrm{2}} ^{\:\mathrm{5}} \:{C}_{\:\mathrm{1}} ^{\:\mathrm{3}} \:=\:\mathrm{45} \\ $$$$ \\ $$$$\:{The}\:{method}\:{above}\:{is}\:{more}\:{comprehensible} \\ $$
