Question Number 49536 by behi83417@gmail.com last updated on 07/Dec/18
Commented by behi83417@gmail.com last updated on 07/Dec/18

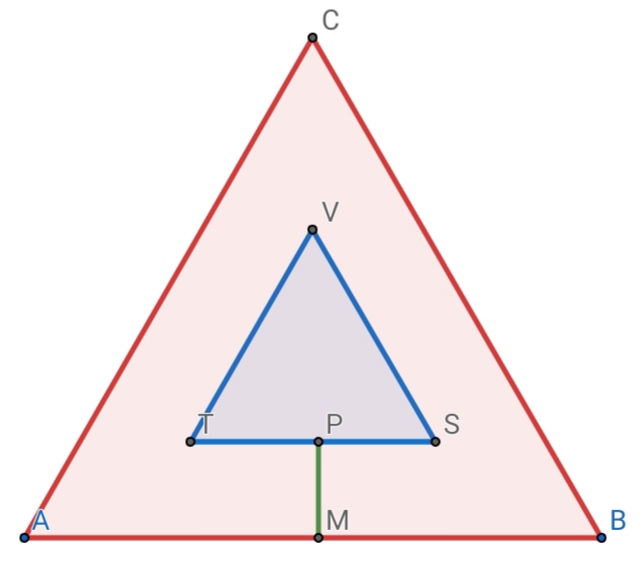
$$\bigtriangleup\:{and}\bigtriangleup\:{are}\:{equilateral}\:{triangles}\:{with} \\ $$$${parallel}\:{sides}\:{and}\:\boldsymbol{\mathrm{PM}},{is}\:{the}\:{same}\:{for} \\ $$$${all}\:{sides}.{if}:{area}\left(\bigtriangleup\right)=\mathrm{32}\:{and}\:{area}\left(\bigtriangleup\right)=\mathrm{6}, \\ $$$${then}:{valve}\:{of}\::\boldsymbol{\mathrm{PM}}=? \\ $$
Commented by Kunal12588 last updated on 07/Dec/18
is answer 1.40704302?
Answered by mr W last updated on 07/Dec/18

$${A}=\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow{a}=\sqrt{\frac{\mathrm{4}{A}}{\:\sqrt{\mathrm{3}}}}=\frac{\mathrm{2}\sqrt{\mathrm{3}\sqrt{\mathrm{3}}{A}}}{\mathrm{3}} \\ $$$${a}_{{red}} =\frac{\mathrm{2}\sqrt{\mathrm{3}\sqrt{\mathrm{3}}×\mathrm{32}}}{\mathrm{3}}=\frac{\mathrm{8}\sqrt{\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{3}} \\ $$$${a}_{{blue}} =\frac{\mathrm{2}\sqrt{\mathrm{3}\sqrt{\mathrm{3}}×\mathrm{6}}}{\mathrm{3}}=\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$${let}\:\delta={PM} \\ $$$${a}_{{red}} −{a}_{{blue}} =\mathrm{2}\sqrt{\mathrm{3}}\delta \\ $$$$\frac{\mathrm{8}\sqrt{\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}=\mathrm{2}\sqrt{\mathrm{3}}\delta \\ $$$$\Rightarrow\delta=\frac{\mathrm{4}\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}−\sqrt{\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{3}}\approx\mathrm{1}.\mathrm{407} \\ $$
Commented by behi83417@gmail.com last updated on 07/Dec/18
$${nice}\:{work}\:{sir}.{thanks}\:{in}\:{advance}. \\ $$
Commented by mr W last updated on 07/Dec/18

$${thank}\:{you}\:{sir}\:{for}\:{checking}\:{it}!\:{it} \\ $$$${is}\:{fixed}\:{now}. \\ $$
Answered by behi83417@gmail.com last updated on 07/Dec/18
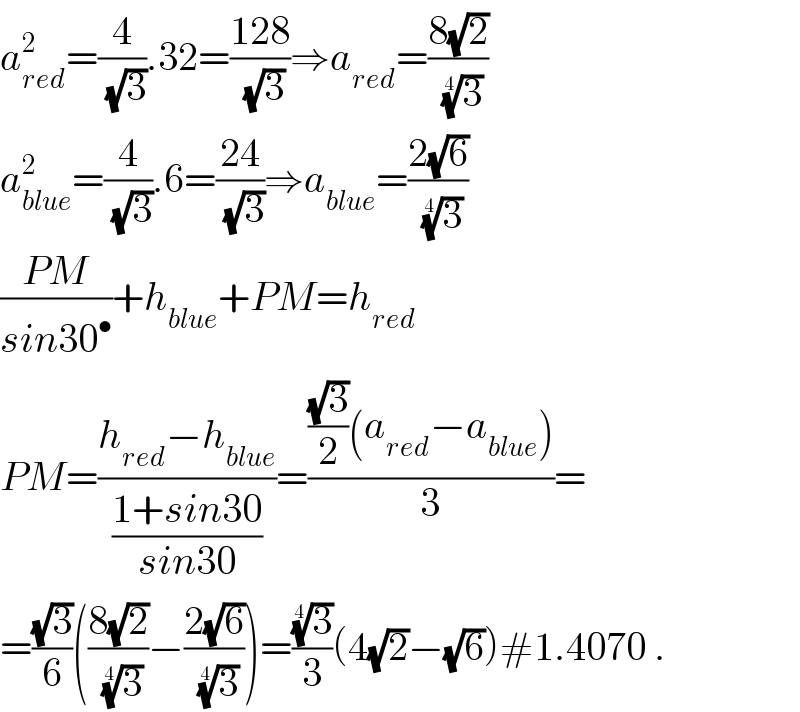
$${a}_{{red}} ^{\mathrm{2}} =\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}.\mathrm{32}=\frac{\mathrm{128}}{\:\sqrt{\mathrm{3}}}\Rightarrow{a}_{{red}} =\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\:\sqrt[{\mathrm{4}}]{\mathrm{3}}} \\ $$$${a}_{{blue}} ^{\mathrm{2}} =\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}.\mathrm{6}=\frac{\mathrm{24}}{\:\sqrt{\mathrm{3}}}\Rightarrow{a}_{{blue}} =\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\:\sqrt[{\mathrm{4}}]{\mathrm{3}}} \\ $$$$\frac{{PM}}{{sin}\mathrm{30}^{\bullet} }+{h}_{{blue}} +{PM}={h}_{{red}} \\ $$$${PM}=\frac{{h}_{{red}} −{h}_{{blue}} }{\frac{\mathrm{1}+{sin}\mathrm{30}}{{sin}\mathrm{30}}}=\frac{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left({a}_{{red}} −{a}_{{blue}} \right)}{\mathrm{3}}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\left(\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\:\sqrt[{\mathrm{4}}]{\mathrm{3}}}−\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\:\sqrt[{\mathrm{4}}]{\mathrm{3}}}\right)=\frac{\sqrt[{\mathrm{4}}]{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{4}\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}\right)#\mathrm{1}.\mathrm{4070}\:. \\ $$
Commented by Kunal12588 last updated on 07/Dec/18
sir what is the meaning of #
Commented by behi83417@gmail.com last updated on 07/Dec/18
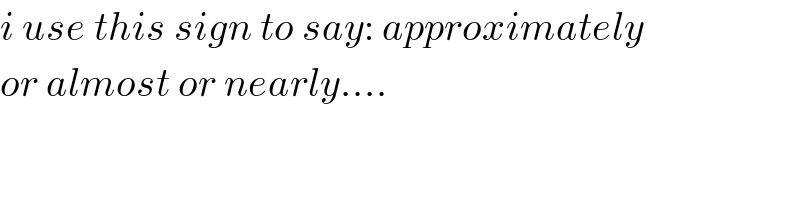
$${i}\:{use}\:{this}\:{sign}\:{to}\:{say}:\:{approximately} \\ $$$${or}\:{almost}\:{or}\:{nearly}…. \\ $$
Answered by Kunal12588 last updated on 08/Dec/18

$${a}_{{blue}} =\sqrt{\frac{\mathrm{24}}{\:\sqrt{\mathrm{3}}}\:},\:{a}_{{red}} =\sqrt{\frac{\mathrm{128}}{\:\sqrt{\mathrm{3}}}} \\ $$$${join}\:{T}\:\&\:{A}\:{and}\:{S}\:\&\:{B}\:,\:{a}_{{red}} \parallel{a}_{{blue}} \\ $$$${so}\:{quad}.{ABST}\:{is}\:{a}\:{trapezium} \\ $$$${ar}\left({ABST}\right)=\frac{\mathrm{1}}{\mathrm{3}}\left\{{ar}\left(\bigtriangleup\right)−{ar}\left(\bigtriangleup\right)\right\}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{32}−\mathrm{6}\right) \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\left({a}_{{blue}} +{a}_{{red}} \right){PM}=\:\frac{\mathrm{26}}{\mathrm{3}} \\ $$$${PM}\left\{\sqrt{\frac{\mathrm{24}}{\:\sqrt{\mathrm{3}}}\:}+\sqrt{\frac{\mathrm{128}}{\:\sqrt{\mathrm{3}}}}\right\}=\frac{\mathrm{52}}{\mathrm{3}} \\ $$$${PM}=\frac{\mathrm{52}}{\mathrm{3}\left(\sqrt{\frac{\mathrm{24}}{\:\sqrt{\mathrm{3}}}\:}+\sqrt{\frac{\mathrm{128}}{\:\sqrt{\mathrm{3}}}}\right)}=\mathrm{1}.\mathrm{40704302}… \\ $$
Commented by Kunal12588 last updated on 08/Dec/18
$${thanks}\:{for}\:{checking}\:{sir} \\ $$
Commented by behi83417@gmail.com last updated on 07/Dec/18
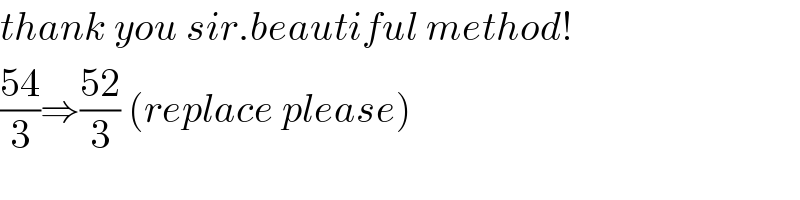
$${thank}\:{you}\:{sir}.{beautiful}\:{method}! \\ $$$$\frac{\mathrm{54}}{\mathrm{3}}\Rightarrow\frac{\mathrm{52}}{\mathrm{3}}\:\left({replace}\:{please}\right) \\ $$
