Question Number 180652 by Shrinava last updated on 14/Nov/22
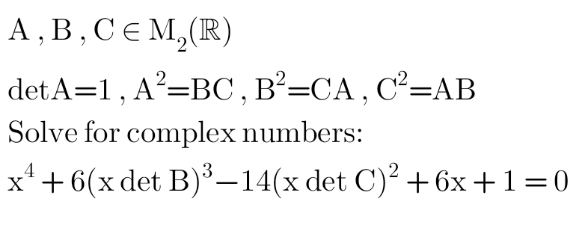
Answered by aleks041103 last updated on 17/Nov/22
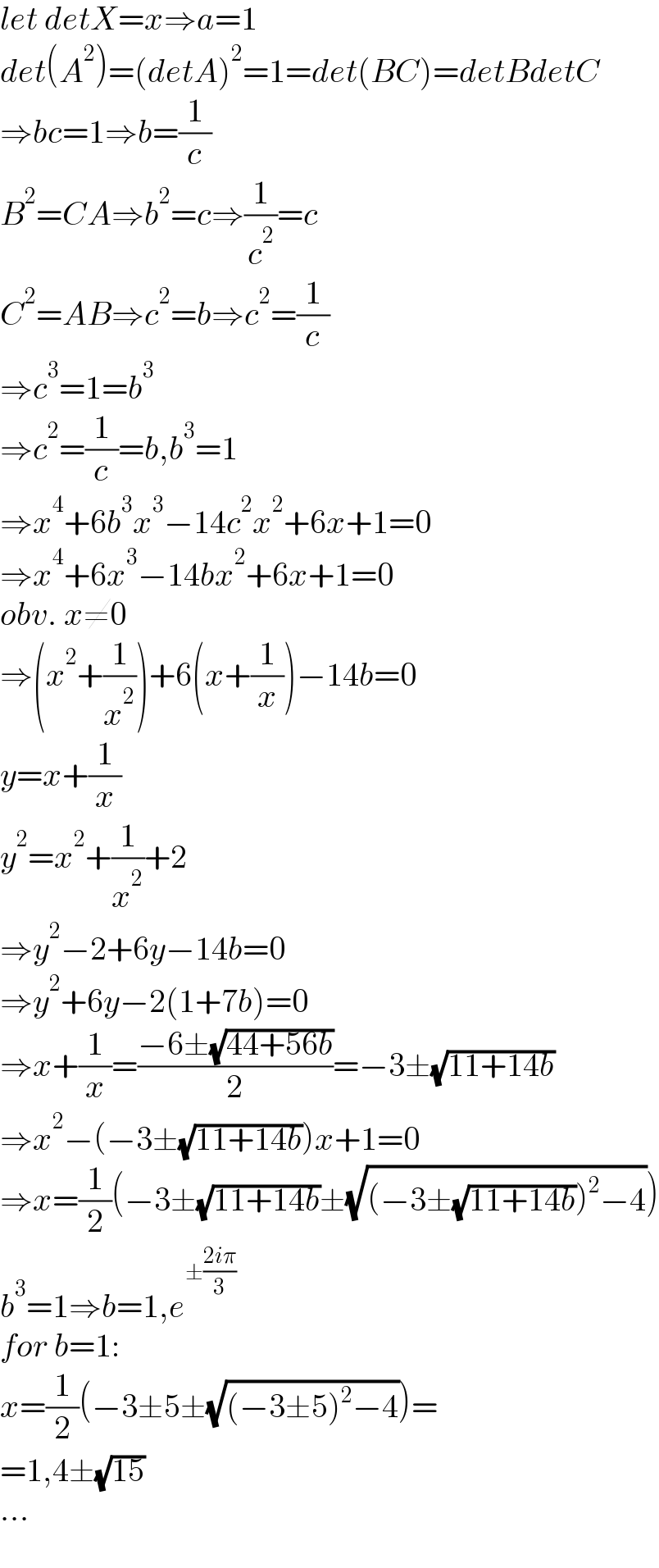
$${let}\:{detX}={x}\Rightarrow{a}=\mathrm{1} \\ $$$${det}\left({A}^{\mathrm{2}} \right)=\left({detA}\right)^{\mathrm{2}} =\mathrm{1}={det}\left({BC}\right)={detBdetC} \\ $$$$\Rightarrow{bc}=\mathrm{1}\Rightarrow{b}=\frac{\mathrm{1}}{{c}} \\ $$$${B}^{\mathrm{2}} ={CA}\Rightarrow{b}^{\mathrm{2}} ={c}\Rightarrow\frac{\mathrm{1}}{{c}^{\mathrm{2}} }={c} \\ $$$${C}^{\mathrm{2}} ={AB}\Rightarrow{c}^{\mathrm{2}} ={b}\Rightarrow{c}^{\mathrm{2}} =\frac{\mathrm{1}}{{c}} \\ $$$$\Rightarrow{c}^{\mathrm{3}} =\mathrm{1}={b}^{\mathrm{3}} \\ $$$$\Rightarrow{c}^{\mathrm{2}} =\frac{\mathrm{1}}{{c}}={b},{b}^{\mathrm{3}} =\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{4}} +\mathrm{6}{b}^{\mathrm{3}} {x}^{\mathrm{3}} −\mathrm{14}{c}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{3}} −\mathrm{14}{bx}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{1}=\mathrm{0} \\ $$$${obv}.\:{x}\neq\mathrm{0} \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)+\mathrm{6}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{14}{b}=\mathrm{0} \\ $$$${y}={x}+\frac{\mathrm{1}}{{x}} \\ $$$${y}^{\mathrm{2}} ={x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{2} \\ $$$$\Rightarrow{y}^{\mathrm{2}} −\mathrm{2}+\mathrm{6}{y}−\mathrm{14}{b}=\mathrm{0} \\ $$$$\Rightarrow{y}^{\mathrm{2}} +\mathrm{6}{y}−\mathrm{2}\left(\mathrm{1}+\mathrm{7}{b}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}+\frac{\mathrm{1}}{{x}}=\frac{−\mathrm{6}\pm\sqrt{\mathrm{44}+\mathrm{56}{b}}}{\mathrm{2}}=−\mathrm{3}\pm\sqrt{\mathrm{11}+\mathrm{14}{b}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\left(−\mathrm{3}\pm\sqrt{\mathrm{11}+\mathrm{14}{b}}\right){x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{3}\pm\sqrt{\mathrm{11}+\mathrm{14}{b}}\pm\sqrt{\left(−\mathrm{3}\pm\sqrt{\mathrm{11}+\mathrm{14}{b}}\right)^{\mathrm{2}} −\mathrm{4}}\right) \\ $$$${b}^{\mathrm{3}} =\mathrm{1}\Rightarrow{b}=\mathrm{1},{e}^{\pm\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} \\ $$$${for}\:{b}=\mathrm{1}: \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{3}\pm\mathrm{5}\pm\sqrt{\left(−\mathrm{3}\pm\mathrm{5}\right)^{\mathrm{2}} −\mathrm{4}}\right)= \\ $$$$=\mathrm{1},\mathrm{4}\pm\sqrt{\mathrm{15}} \\ $$$$… \\ $$
Commented by Shrinava last updated on 17/Nov/22

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{dear}\:\mathrm{professor} \\ $$$$\mathrm{Your}\:\mathrm{solutions}\:\mathrm{are}\:\mathrm{perfect} \\ $$
