Menu Close

Given-that-the-sequence-a-n-is-defined-as-a-1-2-and-a-n-1-a-n-2n-1-for-all-n-1-Find-the-last-two-digits-of-a-100-

Tinku Tara 0 Comments
Pin




Question Number 115133 by ZiYangLee last updated on 23/Sep/20
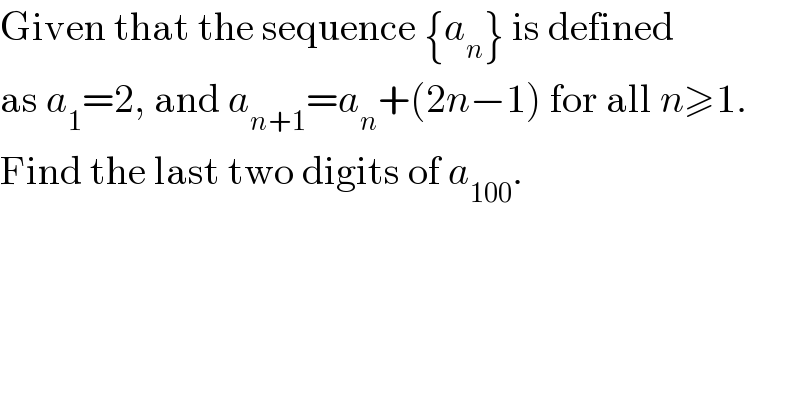
Given that the sequence {a_n } is defined as a_1 =2, and a_(n+1) =a_n +(2n−1) for all n≥1. Find the last two digits of a_(100) .
$$\mathrm{Given}\:\mathrm{that}\:\mathrm{the}\:\mathrm{sequence}\:\left\{{a}_{{n}} \right\}\:\mathrm{is}\:\mathrm{defined} \\ $$$$\mathrm{as}\:{a}_{\mathrm{1}} =\mathrm{2},\:\mathrm{and}\:{a}_{{n}+\mathrm{1}} ={a}_{{n}} +\left(\mathrm{2}{n}−\mathrm{1}\right)\:\mathrm{for}\:\mathrm{all}\:{n}\geqslant\mathrm{1}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{last}\:\mathrm{two}\:\mathrm{digits}\:\mathrm{of}\:{a}_{\mathrm{100}} . \\ $$
Answered by Olaf last updated on 23/Sep/20
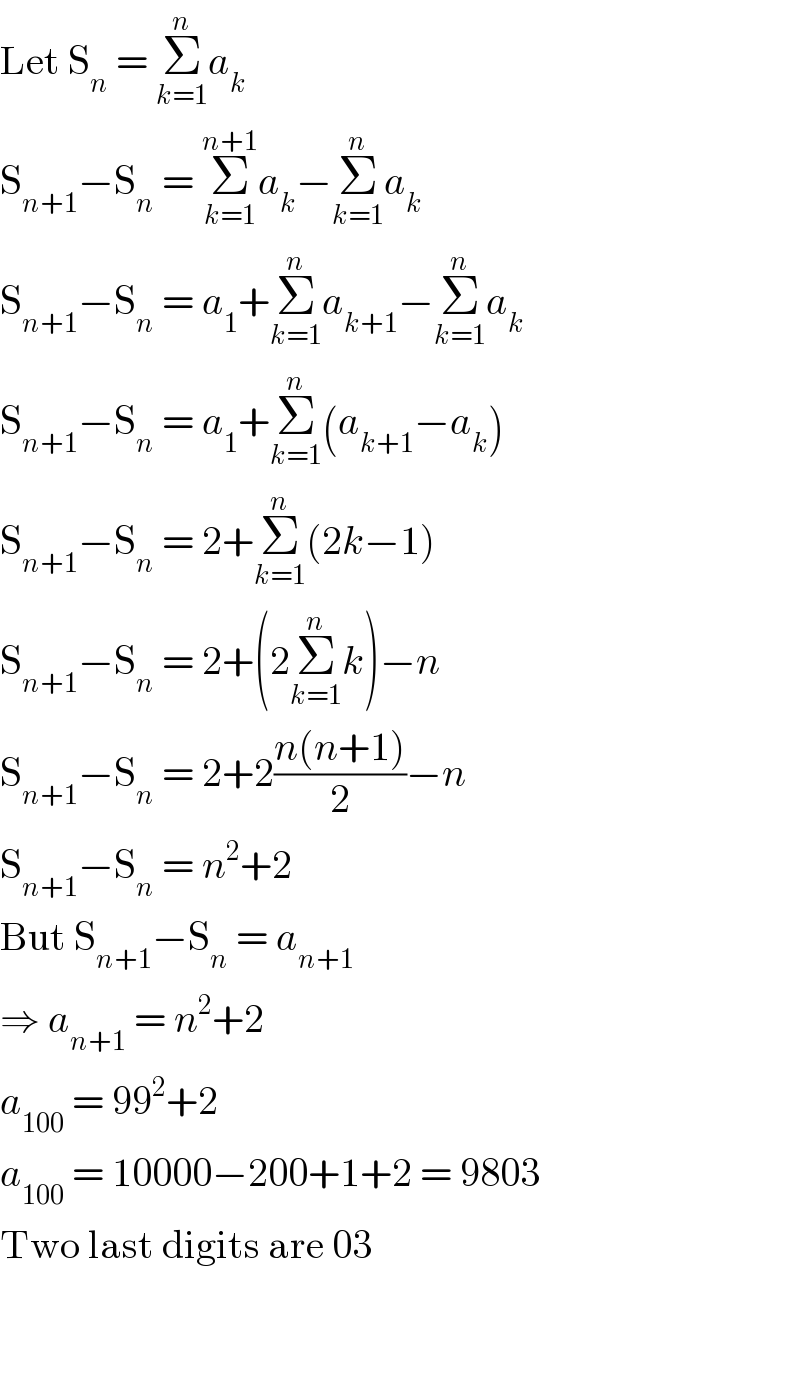
Let S_n = Σ_(k=1) ^n a_k S_(n+1) −S_n = Σ_(k=1) ^(n+1) a_k −Σ_(k=1) ^n a_k S_(n+1) −S_n = a_1 +Σ_(k=1) ^n a_(k+1) −Σ_(k=1) ^n a_k S_(n+1) −S_n = a_1 +Σ_(k=1) ^n (a_(k+1) −a_k ) S_(n+1) −S_n = 2+Σ_(k=1) ^n (2k−1) S_(n+1) −S_n = 2+(2Σ_(k=1) ^n k)−n S_(n+1) −S_n = 2+2((n(n+1))/2)−n S_(n+1) −S_n = n^2 +2 But S_(n+1) −S_n = a_(n+1) ⇒ a_(n+1) = n^2 +2 a_(100) = 99^2 +2 a_(100) = 10000−200+1+2 = 9803 Two last digits are 03
$$\mathrm{Let}\:\mathrm{S}_{{n}} \:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k}} \\ $$$$\mathrm{S}_{{n}+\mathrm{1}} −\mathrm{S}_{{n}} \:=\:\underset{{k}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}{a}_{{k}} −\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k}} \\ $$$$\mathrm{S}_{{n}+\mathrm{1}} −\mathrm{S}_{{n}} \:=\:{a}_{\mathrm{1}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k}+\mathrm{1}} −\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k}} \\ $$$$\mathrm{S}_{{n}+\mathrm{1}} −\mathrm{S}_{{n}} \:=\:{a}_{\mathrm{1}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({a}_{{k}+\mathrm{1}} −{a}_{{k}} \right) \\ $$$$\mathrm{S}_{{n}+\mathrm{1}} −\mathrm{S}_{{n}} \:=\:\mathrm{2}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{2}{k}−\mathrm{1}\right) \\ $$$$\mathrm{S}_{{n}+\mathrm{1}} −\mathrm{S}_{{n}} \:=\:\mathrm{2}+\left(\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\right)−{n} \\ $$$$\mathrm{S}_{{n}+\mathrm{1}} −\mathrm{S}_{{n}} \:=\:\mathrm{2}+\mathrm{2}\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}−{n} \\ $$$$\mathrm{S}_{{n}+\mathrm{1}} −\mathrm{S}_{{n}} \:=\:{n}^{\mathrm{2}} +\mathrm{2} \\ $$$$\mathrm{But}\:\mathrm{S}_{{n}+\mathrm{1}} −\mathrm{S}_{{n}} \:=\:{a}_{{n}+\mathrm{1}} \\ $$$$\Rightarrow\:{a}_{{n}+\mathrm{1}} \:=\:{n}^{\mathrm{2}} +\mathrm{2} \\ $$$${a}_{\mathrm{100}} \:=\:\mathrm{99}^{\mathrm{2}} +\mathrm{2} \\ $$$${a}_{\mathrm{100}} \:=\:\mathrm{10000}−\mathrm{200}+\mathrm{1}+\mathrm{2}\:=\:\mathrm{9803} \\ $$$$\mathrm{Two}\:\mathrm{last}\:\mathrm{digits}\:\mathrm{are}\:\mathrm{03} \\ $$$$ \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 23/Sep/20
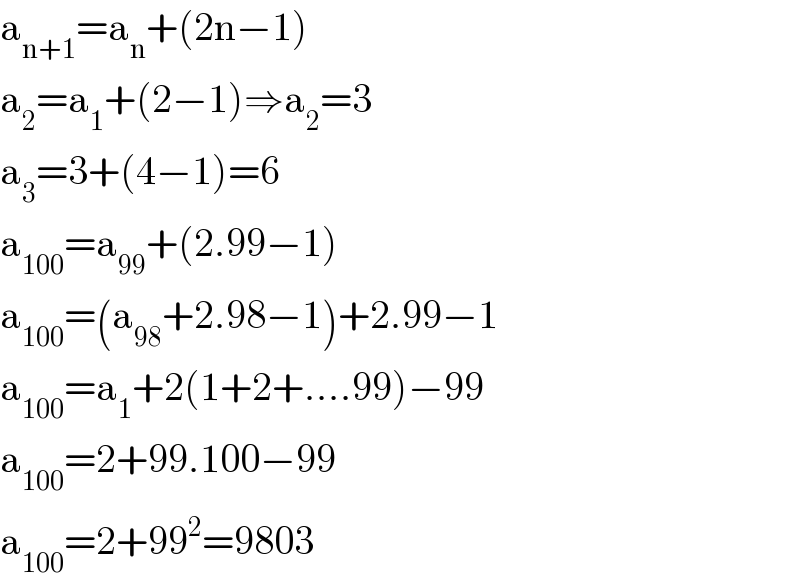
a_(n+1) =a_n +(2n−1) a_2 =a_1 +(2−1)⇒a_2 =3 a_3 =3+(4−1)=6 a_(100) =a_(99) +(2.99−1) a_(100) =(a_(98) +2.98−1)+2.99−1 a_(100) =a_1 +2(1+2+....99)−99 a_(100) =2+99.100−99 a_(100) =2+99^2 =9803
$$\mathrm{a}_{\mathrm{n}+\mathrm{1}} =\mathrm{a}_{\mathrm{n}} +\left(\mathrm{2n}−\mathrm{1}\right) \\ $$$$\mathrm{a}_{\mathrm{2}} =\mathrm{a}_{\mathrm{1}} +\left(\mathrm{2}−\mathrm{1}\right)\Rightarrow\mathrm{a}_{\mathrm{2}} =\mathrm{3} \\ $$$$\mathrm{a}_{\mathrm{3}} =\mathrm{3}+\left(\mathrm{4}−\mathrm{1}\right)=\mathrm{6} \\ $$$$\mathrm{a}_{\mathrm{100}} =\mathrm{a}_{\mathrm{99}} +\left(\mathrm{2}.\mathrm{99}−\mathrm{1}\right) \\ $$$$\mathrm{a}_{\mathrm{100}} =\left(\mathrm{a}_{\mathrm{98}} +\mathrm{2}.\mathrm{98}−\mathrm{1}\right)+\mathrm{2}.\mathrm{99}−\mathrm{1} \\ $$$$\mathrm{a}_{\mathrm{100}} =\mathrm{a}_{\mathrm{1}} +\mathrm{2}\left(\mathrm{1}+\mathrm{2}+….\mathrm{99}\right)−\mathrm{99} \\ $$$$\mathrm{a}_{\mathrm{100}} =\mathrm{2}+\mathrm{99}.\mathrm{100}−\mathrm{99} \\ $$$$\mathrm{a}_{\mathrm{100}} =\mathrm{2}+\mathrm{99}^{\mathrm{2}} =\mathrm{9803} \\ $$
Answered by Bird last updated on 24/Sep/20
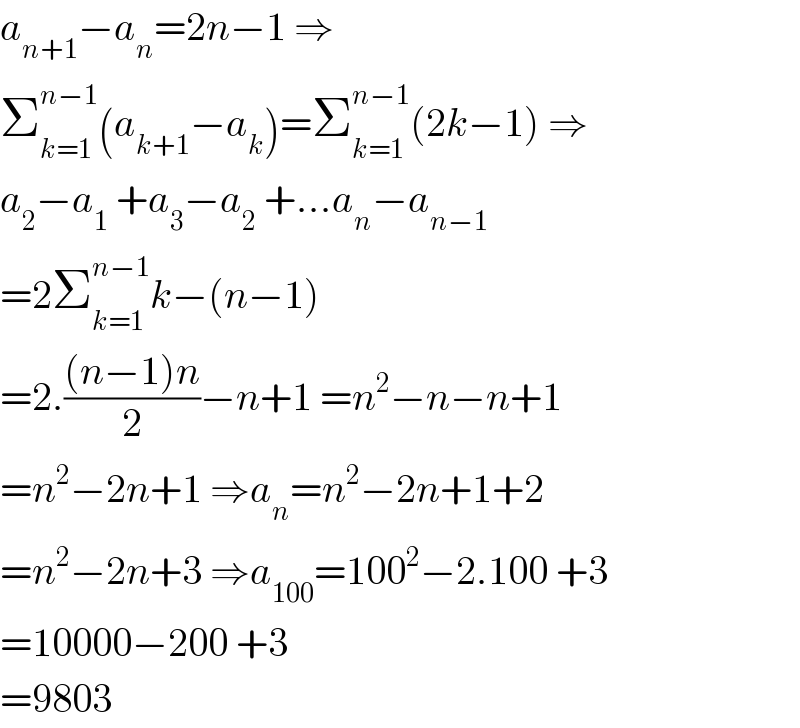
a_(n+1) −a_n =2n−1 ⇒ Σ_(k=1) ^(n−1) (a_(k+1) −a_k )=Σ_(k=1) ^(n−1) (2k−1) ⇒ a_2 −a_1 +a_3 −a_2 +...a_n −a_(n−1) =2Σ_(k=1) ^(n−1) k−(n−1) =2.(((n−1)n)/2)−n+1 =n^2 −n−n+1 =n^2 −2n+1 ⇒a_n =n^2 −2n+1+2 =n^2 −2n+3 ⇒a_(100) =100^2 −2.100 +3 =10000−200 +3 =9803
$${a}_{{n}+\mathrm{1}} −{a}_{{n}} =\mathrm{2}{n}−\mathrm{1}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \left({a}_{{k}+\mathrm{1}} −{a}_{{k}} \right)=\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \left(\mathrm{2}{k}−\mathrm{1}\right)\:\Rightarrow \\ $$$${a}_{\mathrm{2}} −{a}_{\mathrm{1}} \:+{a}_{\mathrm{3}} −{a}_{\mathrm{2}} \:+…{a}_{{n}} −{a}_{{n}−\mathrm{1}} \\ $$$$=\mathrm{2}\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} {k}−\left({n}−\mathrm{1}\right) \\ $$$$=\mathrm{2}.\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}−{n}+\mathrm{1}\:={n}^{\mathrm{2}} −{n}−{n}+\mathrm{1} \\ $$$$={n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}\:\Rightarrow{a}_{{n}} ={n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}+\mathrm{2} \\ $$$$={n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{3}\:\Rightarrow{a}_{\mathrm{100}} =\mathrm{100}^{\mathrm{2}} −\mathrm{2}.\mathrm{100}\:+\mathrm{3} \\ $$$$=\mathrm{10000}−\mathrm{200}\:+\mathrm{3} \\ $$$$=\mathrm{9803} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *