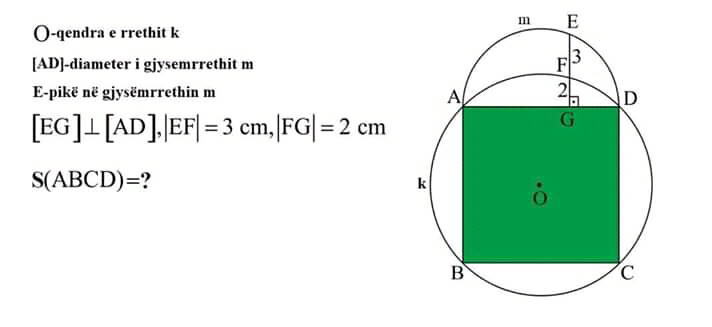
Question Number 49748 by Pk1167156@gmail.com last updated on 10/Dec/18
Answered by MJS last updated on 11/Dec/18
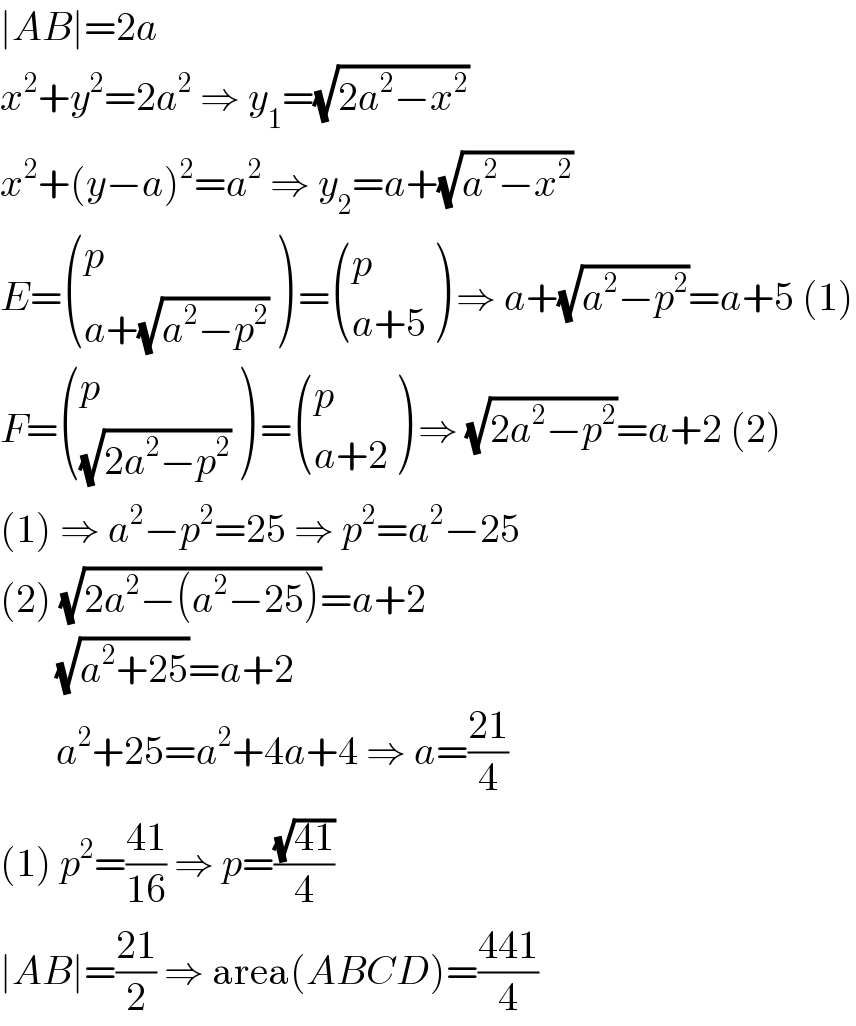
$$\mid{AB}\mid=\mathrm{2}{a} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{2}{a}^{\mathrm{2}} \:\Rightarrow\:{y}_{\mathrm{1}} =\sqrt{\mathrm{2}{a}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} +\left({y}−{a}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \:\Rightarrow\:{y}_{\mathrm{2}} ={a}+\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$${E}=\begin{pmatrix}{{p}}\\{{a}+\sqrt{{a}^{\mathrm{2}} −{p}^{\mathrm{2}} }}\end{pmatrix}\:=\begin{pmatrix}{{p}}\\{{a}+\mathrm{5}}\end{pmatrix}\:\Rightarrow\:{a}+\sqrt{{a}^{\mathrm{2}} −{p}^{\mathrm{2}} }={a}+\mathrm{5}\:\left(\mathrm{1}\right) \\ $$$${F}=\begin{pmatrix}{{p}}\\{\sqrt{\mathrm{2}{a}^{\mathrm{2}} −{p}^{\mathrm{2}} }}\end{pmatrix}\:=\begin{pmatrix}{{p}}\\{{a}+\mathrm{2}}\end{pmatrix}\:\Rightarrow\:\sqrt{\mathrm{2}{a}^{\mathrm{2}} −{p}^{\mathrm{2}} }={a}+\mathrm{2}\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow\:{a}^{\mathrm{2}} −{p}^{\mathrm{2}} =\mathrm{25}\:\Rightarrow\:{p}^{\mathrm{2}} ={a}^{\mathrm{2}} −\mathrm{25} \\ $$$$\left(\mathrm{2}\right)\:\sqrt{\mathrm{2}{a}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −\mathrm{25}\right)}={a}+\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\sqrt{{a}^{\mathrm{2}} +\mathrm{25}}={a}+\mathrm{2} \\ $$$$\:\:\:\:\:\:\:{a}^{\mathrm{2}} +\mathrm{25}={a}^{\mathrm{2}} +\mathrm{4}{a}+\mathrm{4}\:\Rightarrow\:{a}=\frac{\mathrm{21}}{\mathrm{4}} \\ $$$$\left(\mathrm{1}\right)\:{p}^{\mathrm{2}} =\frac{\mathrm{41}}{\mathrm{16}}\:\Rightarrow\:{p}=\frac{\sqrt{\mathrm{41}}}{\mathrm{4}} \\ $$$$\mid{AB}\mid=\frac{\mathrm{21}}{\mathrm{2}}\:\Rightarrow\:\mathrm{area}\left({ABCD}\right)=\frac{\mathrm{441}}{\mathrm{4}} \\ $$
Commented by Pk1167156@gmail.com last updated on 12/Dec/18
thank you Sir
Commented by MJS last updated on 12/Dec/18

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
