Question Number 180873 by Shrinava last updated on 18/Nov/22
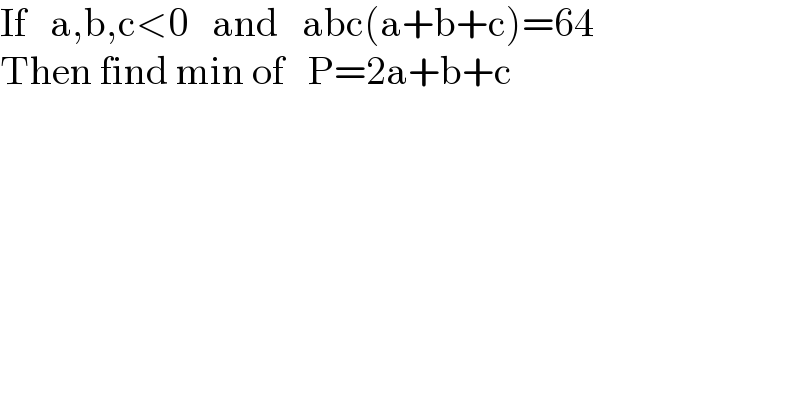
$$\mathrm{If}\:\:\:\mathrm{a},\mathrm{b},\mathrm{c}<\mathrm{0}\:\:\:\mathrm{and}\:\:\:\mathrm{abc}\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)=\mathrm{64} \\ $$$$\mathrm{Then}\:\mathrm{find}\:\mathrm{min}\:\mathrm{of}\:\:\:\mathrm{P}=\mathrm{2a}+\mathrm{b}+\mathrm{c} \\ $$
Commented by mr W last updated on 18/Nov/22
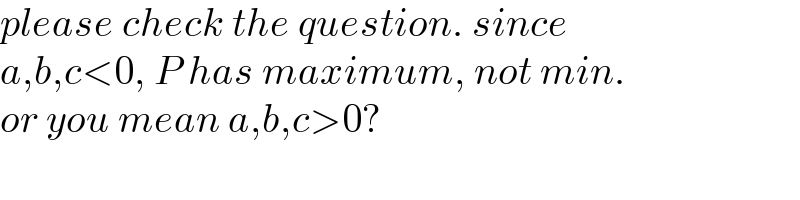
$${please}\:{check}\:{the}\:{question}.\:{since} \\ $$$${a},{b},{c}<\mathrm{0},\:{P}\:{has}\:{maximum},\:{not}\:{min}. \\ $$$${or}\:{you}\:{mean}\:{a},{b},{c}>\mathrm{0}? \\ $$
Commented by Shrinava last updated on 18/Nov/22
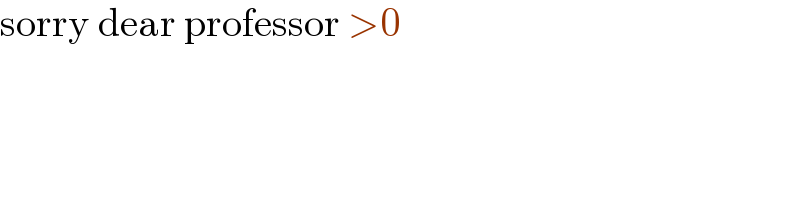
$$\mathrm{sorry}\:\mathrm{dear}\:\mathrm{professor}\:>\mathrm{0} \\ $$
Answered by mr W last updated on 18/Nov/22

$${due}\:{to}\:{symmetry},\:{P}\:{has}\:{extremum} \\ $$$${when}\:{b}={c}={k},\:{say} \\ $$$${P}=\mathrm{2}{a}+{b}+{c}=\mathrm{2}\left({a}+{k}\right) \\ $$$${ak}^{\mathrm{2}} \left({a}+\mathrm{2}{k}\right)=\mathrm{64} \\ $$$${k}^{\mathrm{2}} {a}^{\mathrm{2}} +\mathrm{2}{k}^{\mathrm{3}} {a}−\mathrm{64}=\mathrm{0} \\ $$$$\Rightarrow{a}=\sqrt{{k}^{\mathrm{2}} +\frac{\mathrm{64}}{{k}^{\mathrm{2}} }}−{k} \\ $$$$\Rightarrow{P}=\mathrm{2}\sqrt{{k}^{\mathrm{2}} +\frac{\mathrm{64}}{{k}^{\mathrm{2}} }}\geqslant\mathrm{2}\sqrt{\mathrm{2}×\mathrm{8}}=\mathrm{8}={P}_{{min}} \\ $$
Commented by Shrinava last updated on 18/Nov/22
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{dear}\:\mathrm{professor} \\ $$
