Question Number 49838 by MJS last updated on 11/Dec/18
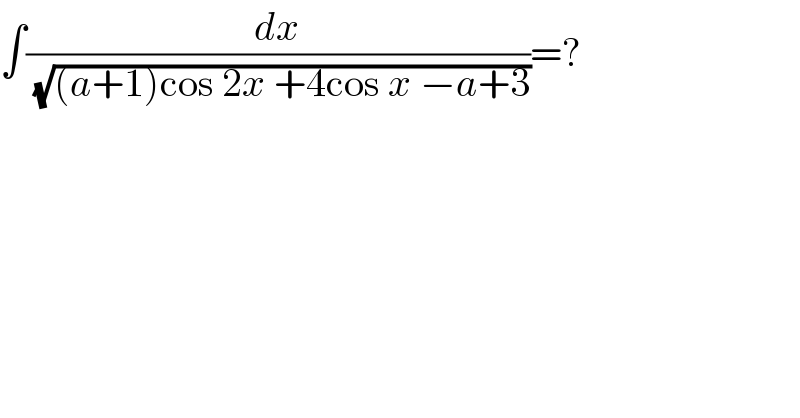
$$\int\frac{{dx}}{\:\sqrt{\left({a}+\mathrm{1}\right)\mathrm{cos}\:\mathrm{2}{x}\:+\mathrm{4cos}\:{x}\:−{a}+\mathrm{3}}}=? \\ $$
Commented by MJS last updated on 11/Dec/18
![∫(dx/( (√((a+1)cos 2x +4cos x −a+3))))= [t=(x/2) → dx=2dt] =2∫(dt/( (√((a+1)cos 4t +4cos 2t −a+3))))= =((√2)/2)∫(dt/(cos t (√((a+1)cos^2 t −a))))= [u=tan t → dt=(du/(u^2 +1)); cos t =(1/( (√(u^2 +1))))] =((√2)/2)∫(du/( (√(1−au^2 ))))= [v=(√a)u → du=(dv/( (√a)))] =(1/( (√(2a))))∫(dv/( (√(1−v^2 ))))=(1/( (√(2a))))arcsin v =(1/( (√(2a))))arcsin ((√a)u) = =(1/( (√(2a))))arcsin ((√a)tan t) =(1/( (√(2a))))arcsin ((√a)tan (x/2)) +C](https://www.tinkutara.com/question/Q49895.png)
$$\int\frac{{dx}}{\:\sqrt{\left({a}+\mathrm{1}\right)\mathrm{cos}\:\mathrm{2}{x}\:+\mathrm{4cos}\:{x}\:−{a}+\mathrm{3}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\mathrm{2}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{\:\sqrt{\left({a}+\mathrm{1}\right)\mathrm{cos}\:\mathrm{4}{t}\:+\mathrm{4cos}\:\mathrm{2}{t}\:−{a}+\mathrm{3}}}= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{dt}}{\mathrm{cos}\:{t}\:\sqrt{\left({a}+\mathrm{1}\right)\mathrm{cos}^{\mathrm{2}} \:{t}\:−{a}}}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{tan}\:{t}\:\rightarrow\:{dt}=\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}};\:\mathrm{cos}\:{t}\:=\frac{\mathrm{1}}{\:\sqrt{{u}^{\mathrm{2}} +\mathrm{1}}}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{du}}{\:\sqrt{\mathrm{1}−{au}^{\mathrm{2}} }}= \\ $$$$\:\:\:\:\:\left[{v}=\sqrt{{a}}{u}\:\rightarrow\:{du}=\frac{{dv}}{\:\sqrt{{a}}}\right] \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{a}}}\int\frac{{dv}}{\:\sqrt{\mathrm{1}−{v}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{a}}}\mathrm{arcsin}\:{v}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{a}}}\mathrm{arcsin}\:\left(\sqrt{{a}}{u}\right)\:= \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{a}}}\mathrm{arcsin}\:\left(\sqrt{{a}}\mathrm{tan}\:{t}\right)\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{a}}}\mathrm{arcsin}\:\left(\sqrt{{a}}\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right)\:+{C} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Dec/18
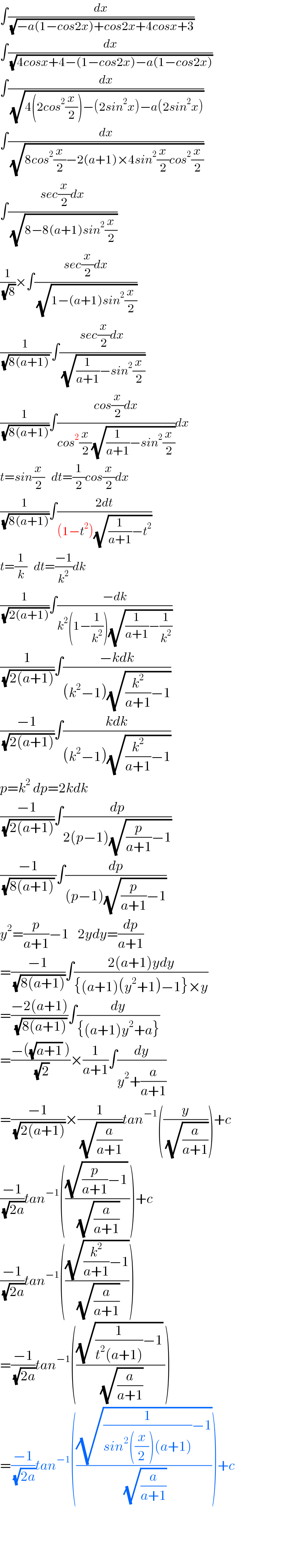
$$\int\frac{{dx}}{\:\sqrt{−{a}\left(\mathrm{1}−{cos}\mathrm{2}{x}\right)+{cos}\mathrm{2}{x}+\mathrm{4}{cosx}+\mathrm{3}}} \\ $$$$\int\frac{{dx}}{\:\sqrt{\mathrm{4}{cosx}+\mathrm{4}−\left(\mathrm{1}−{cos}\mathrm{2}{x}\right)−{a}\left(\mathrm{1}−{cos}\mathrm{2}{x}\right)}} \\ $$$$\int\frac{{dx}}{\:\sqrt{\mathrm{4}\left(\mathrm{2}{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right)−\left(\mathrm{2}{sin}^{\mathrm{2}} {x}\right)−{a}\left(\mathrm{2}{sin}^{\mathrm{2}} {x}\right)}} \\ $$$$\int\frac{{dx}}{\:\sqrt{\mathrm{8}{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{2}\left({a}+\mathrm{1}\right)×\mathrm{4}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}} \\ $$$$\int\frac{{sec}\frac{{x}}{\mathrm{2}}{dx}}{\:\sqrt{\mathrm{8}−\mathrm{8}\left({a}+\mathrm{1}\right){sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{8}}}×\int\frac{{sec}\frac{{x}}{\mathrm{2}}{dx}}{\:\sqrt{\mathrm{1}−\left({a}+\mathrm{1}\right){sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{8}\left({a}+\mathrm{1}\right)}\:}\int\frac{{sec}\frac{{x}}{\mathrm{2}}{dx}}{\:\sqrt{\frac{\mathrm{1}}{{a}+\mathrm{1}}−{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{8}\left({a}+\mathrm{1}\right)}}\int\frac{{cos}\frac{{x}}{\mathrm{2}}{dx}}{{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{{a}+\mathrm{1}}−{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}}{dx} \\ $$$${t}={sin}\frac{{x}}{\mathrm{2}}\:\:\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}{dx} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{8}\left({a}+\mathrm{1}\right)}}\int\frac{\mathrm{2}{dt}}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\sqrt{\frac{\mathrm{1}}{{a}+\mathrm{1}}−{t}^{\mathrm{2}} }} \\ $$$${t}=\frac{\mathrm{1}}{{k}}\:\:\:{dt}=\frac{−\mathrm{1}}{{k}^{\mathrm{2}} }{dk} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\left({a}+\mathrm{1}\right)}}\int\frac{−{dk}}{{k}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\right)\sqrt{\frac{\mathrm{1}}{{a}+\mathrm{1}}−\frac{\mathrm{1}}{{k}^{\mathrm{2}} }}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\left({a}+\mathrm{1}\right)}}\int\frac{−{kdk}}{\left({k}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\frac{{k}^{\mathrm{2}} }{{a}+\mathrm{1}}−\mathrm{1}}} \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}\left({a}+\mathrm{1}\right)}}\int\frac{{kdk}}{\left({k}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\frac{{k}^{\mathrm{2}} }{{a}+\mathrm{1}}−\mathrm{1}}} \\ $$$${p}={k}^{\mathrm{2}} \:{dp}=\mathrm{2}{kdk} \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}\left({a}+\mathrm{1}\right)}}\int\frac{{dp}}{\mathrm{2}\left({p}−\mathrm{1}\right)\sqrt{\frac{{p}}{{a}+\mathrm{1}}−\mathrm{1}}} \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{\mathrm{8}\left({a}+\mathrm{1}\right)}\:}\int\frac{{dp}}{\left({p}−\mathrm{1}\right)\sqrt{\frac{{p}}{{a}+\mathrm{1}}−\mathrm{1}}} \\ $$$${y}^{\mathrm{2}} =\frac{{p}}{{a}+\mathrm{1}}−\mathrm{1}\:\:\:\:\mathrm{2}{ydy}=\frac{{dp}}{{a}+\mathrm{1}} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{8}\left({a}+\mathrm{1}\right)}}\int\frac{\mathrm{2}\left({a}+\mathrm{1}\right){ydy}}{\left\{\left({a}+\mathrm{1}\right)\left({y}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{1}\right\}×{y}} \\ $$$$=\frac{−\mathrm{2}\left({a}+\mathrm{1}\right)}{\:\sqrt{\mathrm{8}\left({a}+\mathrm{1}\right)}}\int\frac{{dy}}{\left\{\left({a}+\mathrm{1}\right){y}^{\mathrm{2}} +{a}\right\}} \\ $$$$=\frac{−\left(\sqrt{{a}+\mathrm{1}}\:\right)}{\:\sqrt{\mathrm{2}}}×\frac{\mathrm{1}}{{a}+\mathrm{1}}\int\frac{{dy}}{{y}^{\mathrm{2}} +\frac{{a}}{{a}+\mathrm{1}}} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}\left({a}+\mathrm{1}\right)}}×\frac{\mathrm{1}}{\:\sqrt{\frac{{a}}{{a}+\mathrm{1}}}}{tan}^{−\mathrm{1}} \left(\frac{{y}}{\:\sqrt{\frac{{a}}{{a}+\mathrm{1}}}}\right)+{c} \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}{a}}}{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\frac{{p}}{{a}+\mathrm{1}}−\mathrm{1}}\:}{\:\sqrt{\frac{{a}}{{a}+\mathrm{1}}}}\right)+{c} \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}{a}}}{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\frac{{k}^{\mathrm{2}} }{{a}+\mathrm{1}}−\mathrm{1}}}{\:\sqrt{\frac{{a}}{{a}+\mathrm{1}}}}\right) \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}{a}}}{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{2}} \left({a}+\mathrm{1}\right)}−\mathrm{1}}\:}{\:\sqrt{\frac{{a}}{{a}+\mathrm{1}}}}\right) \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}{a}}}{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\left({a}+\mathrm{1}\right)}−\mathrm{1}}}{\:\sqrt{\frac{{a}}{{a}+\mathrm{1}}}}\right)+{c} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by MJS last updated on 11/Dec/18
$$\mathrm{correct},\:\mathrm{thank}\:\mathrm{you}! \\ $$
Commented by malwaan last updated on 12/Dec/18

$$\mathrm{great} \\ $$$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 12/Dec/18
$${MJS}\:{sir}\:{your}\:{method}\:{is}\:{short}\:{and}\:{tricky}, \\ $$$${thank}\:{you}\:{sir}… \\ $$
Commented by MJS last updated on 12/Dec/18
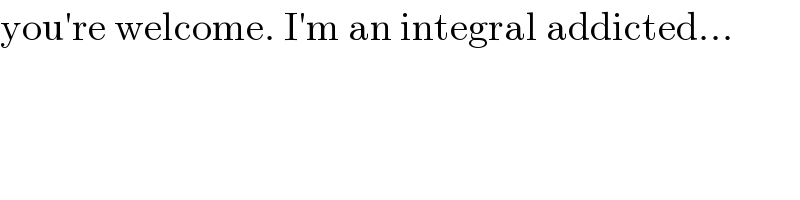
$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome}.\:\mathrm{I}'\mathrm{m}\:\mathrm{an}\:\mathrm{integral}\:\mathrm{addicted}… \\ $$
