Question Number 181323 by KONE last updated on 24/Nov/22

$$\begin{cases}{{U}_{\mathrm{0}} =\mathrm{1}\:{et}\:{U}_{\mathrm{1}} =\mathrm{2}}\\{{U}_{{n}+\mathrm{2}} =\sqrt{{U}_{{n}} {U}_{{n}+\mathrm{1}} }}\end{cases} \\ $$$${determiner}\:{le}\:{terme}\:{generale}\:{et}\:{sa}\:{nature} \\ $$$${besoin}\:{d}'{aide}\:{avp} \\ $$
Commented by KONE last updated on 24/Nov/22

$$\bullet{svp} \\ $$
Answered by Frix last updated on 24/Nov/22
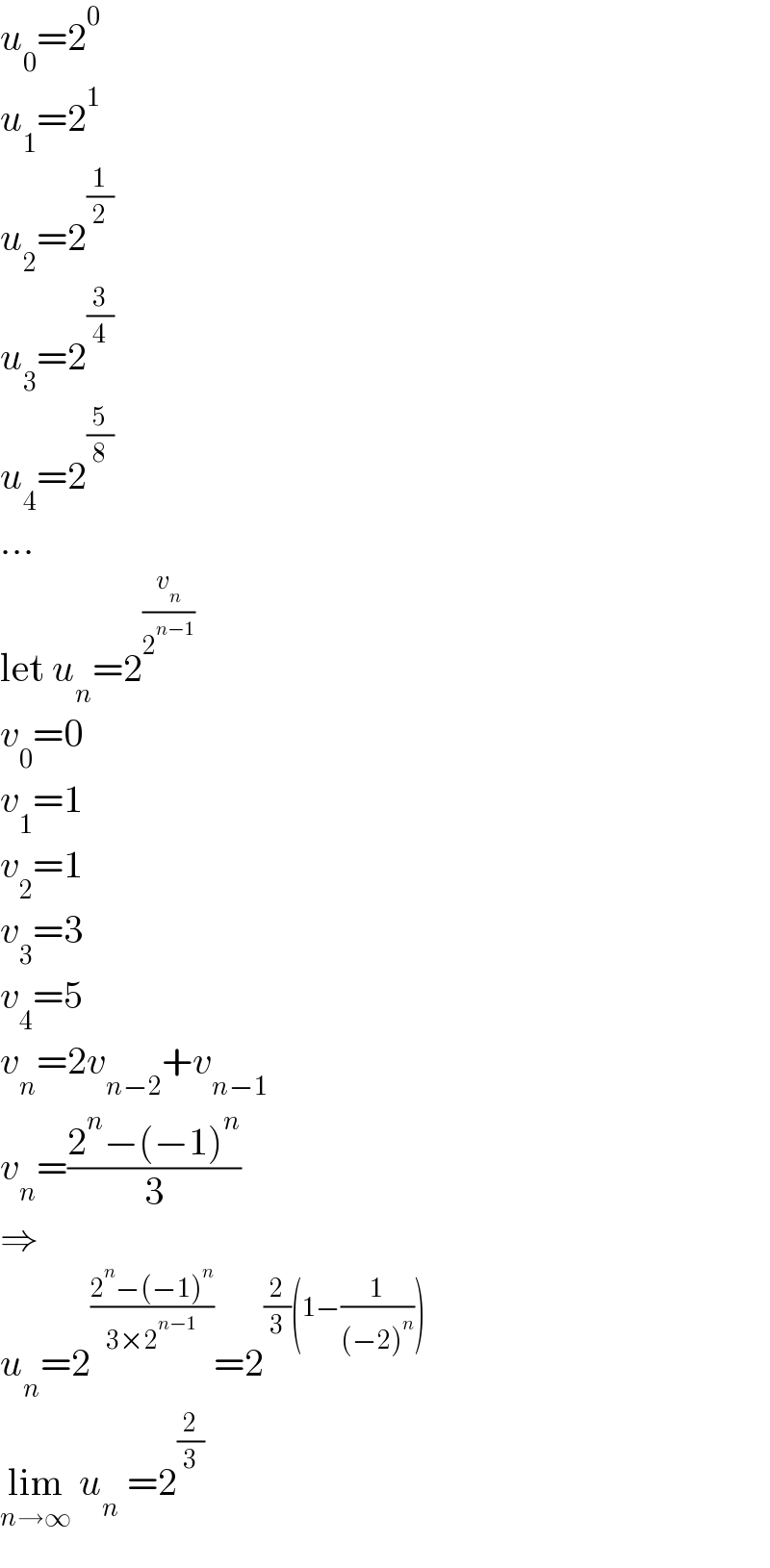
$${u}_{\mathrm{0}} =\mathrm{2}^{\mathrm{0}} \\ $$$${u}_{\mathrm{1}} =\mathrm{2}^{\mathrm{1}} \\ $$$${u}_{\mathrm{2}} =\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${u}_{\mathrm{3}} =\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$${u}_{\mathrm{4}} =\mathrm{2}^{\frac{\mathrm{5}}{\mathrm{8}}} \\ $$$$… \\ $$$$\mathrm{let}\:{u}_{{n}} =\mathrm{2}^{\frac{{v}_{{n}} }{\mathrm{2}^{{n}−\mathrm{1}} }} \\ $$$${v}_{\mathrm{0}} =\mathrm{0} \\ $$$${v}_{\mathrm{1}} =\mathrm{1} \\ $$$${v}_{\mathrm{2}} =\mathrm{1} \\ $$$${v}_{\mathrm{3}} =\mathrm{3} \\ $$$${v}_{\mathrm{4}} =\mathrm{5} \\ $$$${v}_{{n}} =\mathrm{2}{v}_{{n}−\mathrm{2}} +{v}_{{n}−\mathrm{1}} \\ $$$${v}_{{n}} =\frac{\mathrm{2}^{{n}} −\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}} \\ $$$$\Rightarrow \\ $$$${u}_{{n}} =\mathrm{2}^{\frac{\mathrm{2}^{{n}} −\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}×\mathrm{2}^{{n}−\mathrm{1}} }} =\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−\frac{\mathrm{1}}{\left(−\mathrm{2}\right)^{{n}} }\right)} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{u}_{{n}} \:=\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$
Commented by KONE last updated on 25/Nov/22

$${merci} \\ $$
Answered by mr W last updated on 24/Nov/22
![U_(n+2) =(√(U_(n+1) U_n )) ln U_(n+2) =(1/2)(ln U_(n+1) +ln U_n ) let a_n =ln U_n 2a_(n+2) −a_(n+1) −a_n =0 let a_n =Cp^n 2Cp^(n+2) −Cp^(n+1) −Cp^n =0 Cp^n (2p^2 −p−1)=0 2p^2 −p−1=0 (2p+1)(p−1)=0 ⇒p=−(1/2) or 1 ⇒a_n =C×(−(1/2))^n +D×(1)^n =(C/((−2)^n ))+D a_0 =ln U_0 =ln 1=0=(C/((−2)^0 ))+D ⇒C+D=0 ...(i) a_1 =ln U_1 =ln 2=(C/((−2)^1 ))+D=−(C/2)+D ⇒−C+2D=2ln 2 ...(ii) ⇒D=((2ln 2)/3) ⇒C=−((2ln 2)/3) ⇒a_n =((2ln 2)/3)(1−(((−1)^n )/2^n ))=ln 2^((2/3)(1−(((−1)^n )/2^n ))) ⇒U_n =e^a_n =2^((2/3)[1−(((−1)^n )/2^n )]) ✓ lim_(n→∞) U_n =2^(2/3) =(4)^(1/3)](https://www.tinkutara.com/question/Q181351.png)
$${U}_{{n}+\mathrm{2}} =\sqrt{{U}_{{n}+\mathrm{1}} {U}_{{n}} } \\ $$$$\mathrm{ln}\:{U}_{{n}+\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\:{U}_{{n}+\mathrm{1}} +\mathrm{ln}\:{U}_{{n}} \right) \\ $$$${let}\:{a}_{{n}} =\mathrm{ln}\:{U}_{{n}} \\ $$$$\mathrm{2}{a}_{{n}+\mathrm{2}} −{a}_{{n}+\mathrm{1}} −{a}_{{n}} =\mathrm{0} \\ $$$${let}\:{a}_{{n}} ={Cp}^{{n}} \\ $$$$\mathrm{2}{Cp}^{{n}+\mathrm{2}} −{Cp}^{{n}+\mathrm{1}} −{Cp}^{{n}} =\mathrm{0} \\ $$$${Cp}^{{n}} \left(\mathrm{2}{p}^{\mathrm{2}} −{p}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{2}{p}^{\mathrm{2}} −{p}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}{p}+\mathrm{1}\right)\left({p}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{p}=−\frac{\mathrm{1}}{\mathrm{2}}\:{or}\:\mathrm{1} \\ $$$$\Rightarrow{a}_{{n}} ={C}×\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} +{D}×\left(\mathrm{1}\right)^{{n}} =\frac{{C}}{\left(−\mathrm{2}\right)^{{n}} }+{D} \\ $$$${a}_{\mathrm{0}} =\mathrm{ln}\:{U}_{\mathrm{0}} =\mathrm{ln}\:\mathrm{1}=\mathrm{0}=\frac{{C}}{\left(−\mathrm{2}\right)^{\mathrm{0}} }+{D} \\ $$$$\Rightarrow{C}+{D}=\mathrm{0}\:\:\:…\left({i}\right) \\ $$$${a}_{\mathrm{1}} =\mathrm{ln}\:{U}_{\mathrm{1}} =\mathrm{ln}\:\mathrm{2}=\frac{{C}}{\left(−\mathrm{2}\right)^{\mathrm{1}} }+{D}=−\frac{{C}}{\mathrm{2}}+{D} \\ $$$$\Rightarrow−{C}+\mathrm{2}{D}=\mathrm{2ln}\:\mathrm{2}\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow{D}=\frac{\mathrm{2ln}\:\mathrm{2}}{\mathrm{3}}\:\Rightarrow{C}=−\frac{\mathrm{2ln}\:\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{a}_{{n}} =\frac{\mathrm{2ln}\:\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }\right)=\mathrm{ln}\:\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }\right)} \\ $$$$\Rightarrow{U}_{{n}} ={e}^{{a}_{{n}} } =\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}\left[\mathrm{1}−\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }\right]} \:\checkmark \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{U}_{{n}} =\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} =\sqrt[{\mathrm{3}}]{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 24/Nov/22

$$\:\:{sir}\:{W}\:\:\:\left(\:{excuse}\:{me}\:\right) \\ $$$$\:\:\:\:{e}^{\:{a}_{{n}} } \:=\:\sqrt[{\mathrm{3}}]{\mathrm{4}}\:.\:{e}^{\:\mathrm{1}−\frac{\left(−\mathrm{1}\right)^{\:{n}} }{\mathrm{2}^{\:{n}} }} \:??? \\ $$
Commented by mnjuly1970 last updated on 24/Nov/22
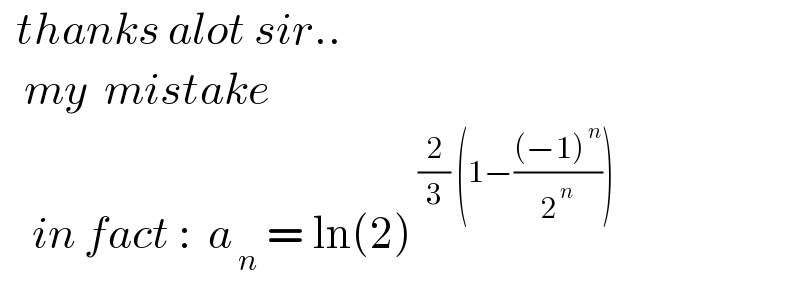
$$\:\:{thanks}\:{alot}\:{sir}.. \\ $$$$\:\:\:{my}\:\:{mistake} \\ $$$$\:\:\:\:{in}\:{fact}\::\:\:{a}_{\:{n}} \:=\:\mathrm{ln}\left(\mathrm{2}\right)^{\:\frac{\mathrm{2}}{\mathrm{3}}\:\left(\mathrm{1}−\frac{\left(−\mathrm{1}\right)^{\:{n}} }{\mathrm{2}^{\:{n}} }\right)} \\ $$
Commented by mr W last updated on 24/Nov/22
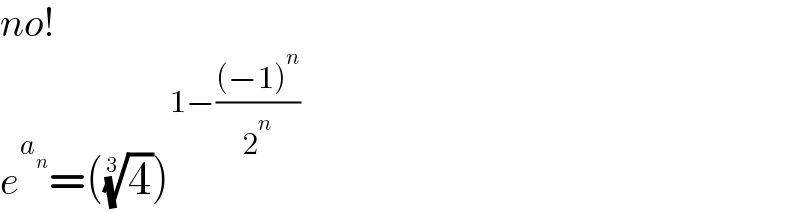
$${no}!\: \\ $$$${e}^{{a}_{{n}} } =\left(\sqrt[{\mathrm{3}}]{\mathrm{4}}\right)^{\mathrm{1}−\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }} \\ $$
Commented by mnjuly1970 last updated on 24/Nov/22

Commented by KONE last updated on 25/Nov/22

$${merci} \\ $$
