Question Number 115817 by A8;15: last updated on 28/Sep/20

Commented by Dwaipayan Shikari last updated on 28/Sep/20

$$\mathrm{Sorry},\:\mathrm{I}\:\:\mathrm{haven}'\mathrm{t}\:\mathrm{found}\:\mathrm{any}\:\mathrm{symmetry} \\ $$$$\mathrm{So}\:\mathrm{i}\:\mathrm{started}\:\mathrm{with}\:\mathrm{if}\:\mathrm{the}\:\mathrm{question}\:\mathrm{becomes}… \\ $$
Commented by Dwaipayan Shikari last updated on 28/Sep/20
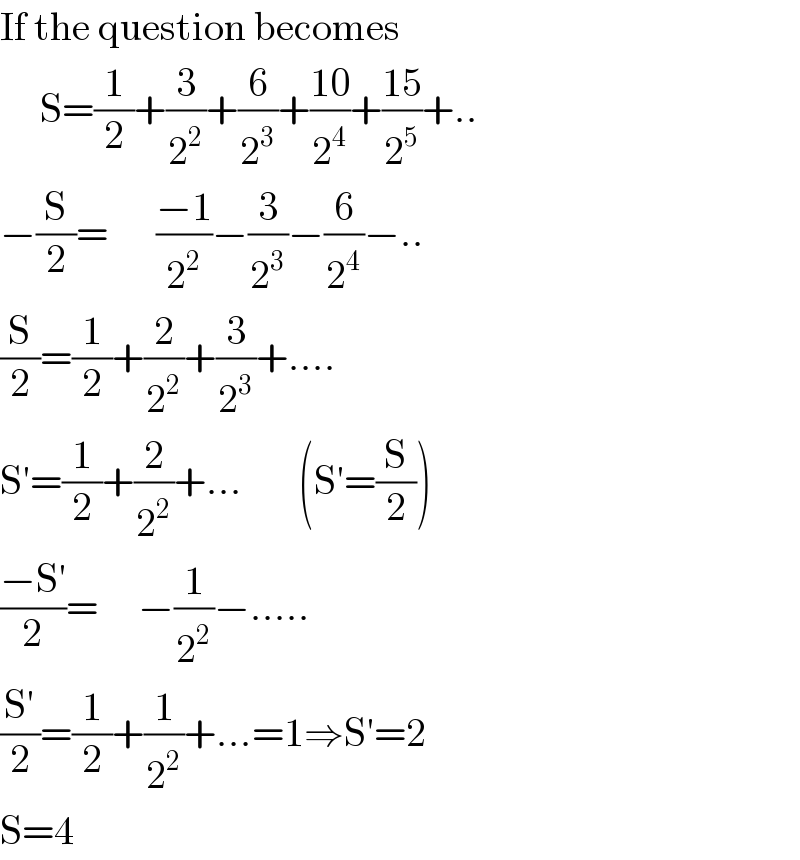
$$\mathrm{If}\:\mathrm{the}\:\mathrm{question}\:\mathrm{becomes}\: \\ $$$$\:\:\:\:\:\mathrm{S}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{6}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{10}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{15}}{\mathrm{2}^{\mathrm{5}} }+.. \\ $$$$−\frac{\mathrm{S}}{\mathrm{2}}=\:\:\:\:\:\:\frac{−\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }−\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }−\frac{\mathrm{6}}{\mathrm{2}^{\mathrm{4}} }−.. \\ $$$$\frac{\mathrm{S}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+…. \\ $$$$\mathrm{S}'=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+…\:\:\:\:\:\:\:\left(\mathrm{S}'=\frac{\mathrm{S}}{\mathrm{2}}\right) \\ $$$$\frac{−\mathrm{S}'}{\mathrm{2}}=\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }−….. \\ $$$$\frac{\mathrm{S}'}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+…=\mathrm{1}\Rightarrow\mathrm{S}'=\mathrm{2} \\ $$$$\mathrm{S}=\mathrm{4} \\ $$
Commented by A8;15: last updated on 28/Sep/20
this is a another solution
Commented by A8;15: last updated on 28/Sep/20
you send me solution of another question
Commented by MJS_new last updated on 28/Sep/20
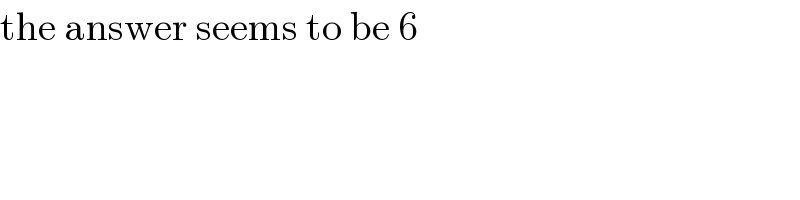
$$\mathrm{the}\:\mathrm{answer}\:\mathrm{seems}\:\mathrm{to}\:\mathrm{be}\:\mathrm{6} \\ $$
Commented by prakash jain last updated on 28/Sep/20
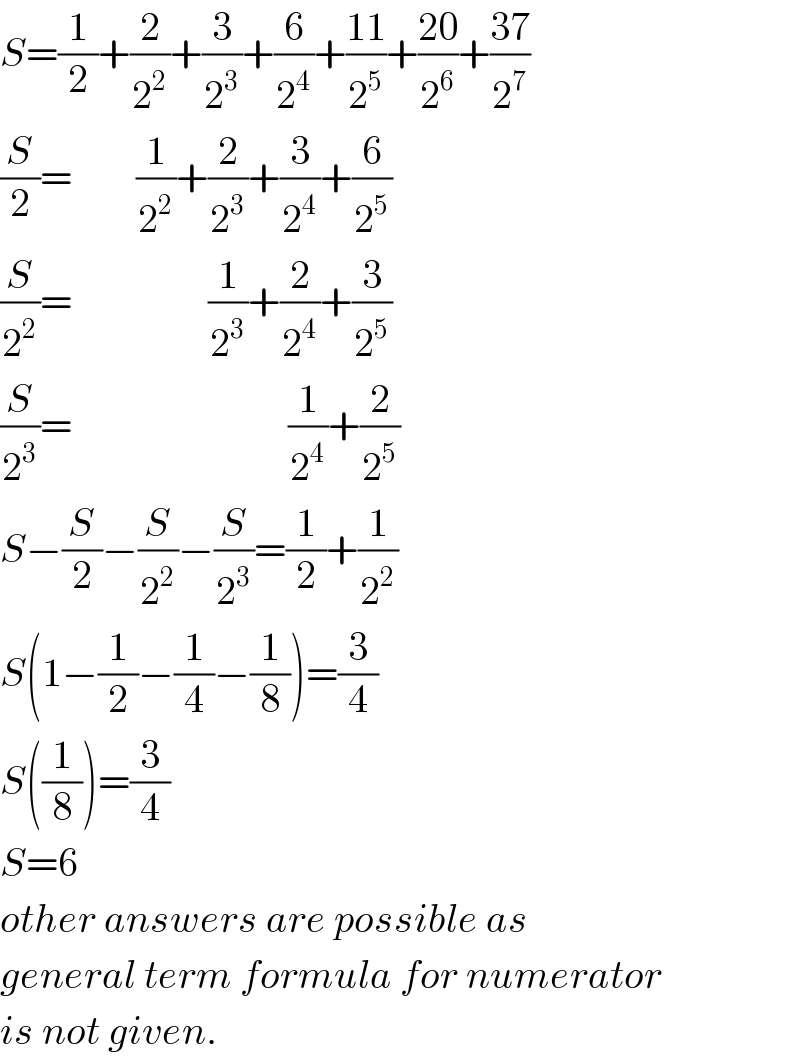
$${S}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{6}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{11}}{\mathrm{2}^{\mathrm{5}} }+\frac{\mathrm{20}}{\mathrm{2}^{\mathrm{6}} }+\frac{\mathrm{37}}{\mathrm{2}^{\mathrm{7}} } \\ $$$$\frac{{S}}{\mathrm{2}}=\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{6}}{\mathrm{2}^{\mathrm{5}} } \\ $$$$\frac{{S}}{\mathrm{2}^{\mathrm{2}} }=\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{5}} } \\ $$$$\frac{{S}}{\mathrm{2}^{\mathrm{3}} }=\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{5}} }\: \\ $$$${S}−\frac{{S}}{\mathrm{2}}−\frac{{S}}{\mathrm{2}^{\mathrm{2}} }−\frac{{S}}{\mathrm{2}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} } \\ $$$${S}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}}\right)=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${S}\left(\frac{\mathrm{1}}{\mathrm{8}}\right)=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${S}=\mathrm{6} \\ $$$${other}\:{answers}\:{are}\:{possible}\:{as} \\ $$$${general}\:{term}\:{formula}\:{for}\:{numerator} \\ $$$${is}\:{not}\:{given}. \\ $$
Commented by MJS_new last updated on 28/Sep/20
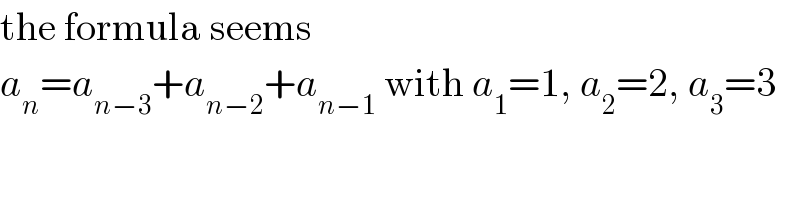
$$\mathrm{the}\:\mathrm{formula}\:\mathrm{seems} \\ $$$${a}_{{n}} ={a}_{{n}−\mathrm{3}} +{a}_{{n}−\mathrm{2}} +{a}_{{n}−\mathrm{1}} \:\mathrm{with}\:{a}_{\mathrm{1}} =\mathrm{1},\:{a}_{\mathrm{2}} =\mathrm{2},\:{a}_{\mathrm{3}} =\mathrm{3} \\ $$
Commented by prakash jain last updated on 28/Sep/20

$$\mathrm{Yes}.\:\mathrm{That}\:\mathrm{is}\:\mathrm{what}\:\mathrm{i}\:\mathrm{used}\:\mathrm{but}\:\mathrm{you},\:\mathrm{i} \\ $$$$\mathrm{and}\:\mathrm{several}\:\mathrm{other}\:\mathrm{users}\:\mathrm{have}\:\mathrm{stated} \\ $$$$\mathrm{if}\:\mathrm{a}\:\mathrm{finite}\:\mathrm{set}\:\mathrm{of}\:\mathrm{terms}\:\mathrm{are}\:\mathrm{given}\:\mathrm{then} \\ $$$$\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{unique}\:\mathrm{formula}. \\ $$$${a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ,….,{a}_{{k}} \:\mathrm{are}\:\mathrm{given} \\ $$$$\mathrm{and}\:{g}\left({n}\right)\:\mathrm{is}\:\mathrm{one}\:\mathrm{formuala}\:\mathrm{such}\:\mathrm{that} \\ $$$${g}\left({i}\right)={a}_{{i}} \:,\:\:\:\:\mathrm{1}\leqslant{i}\leqslant{k} \\ $$$${then} \\ $$$${f}\left({n}\right)={g}\left({n}\right)+{h}\left({n}\right)\underset{{i}=\mathrm{1}} {\overset{{k}} {\prod}}\left({n}−{k}\right) \\ $$$$\mathrm{is}\:\mathrm{also}\:\mathrm{a}\:\mathrm{formula}\:\mathrm{where}\:{h}\left({n}\right)\:\mathrm{is} \\ $$$$\mathrm{any}\:\mathrm{arbitarary}\:\mathrm{function}\:\mathrm{of}\:{n}. \\ $$
Commented by MJS_new last updated on 28/Sep/20

$$\mathrm{of}\:\mathrm{course}\:\mathrm{you}\:\mathrm{are}\:\mathrm{right} \\ $$
Answered by Olaf last updated on 29/Sep/20
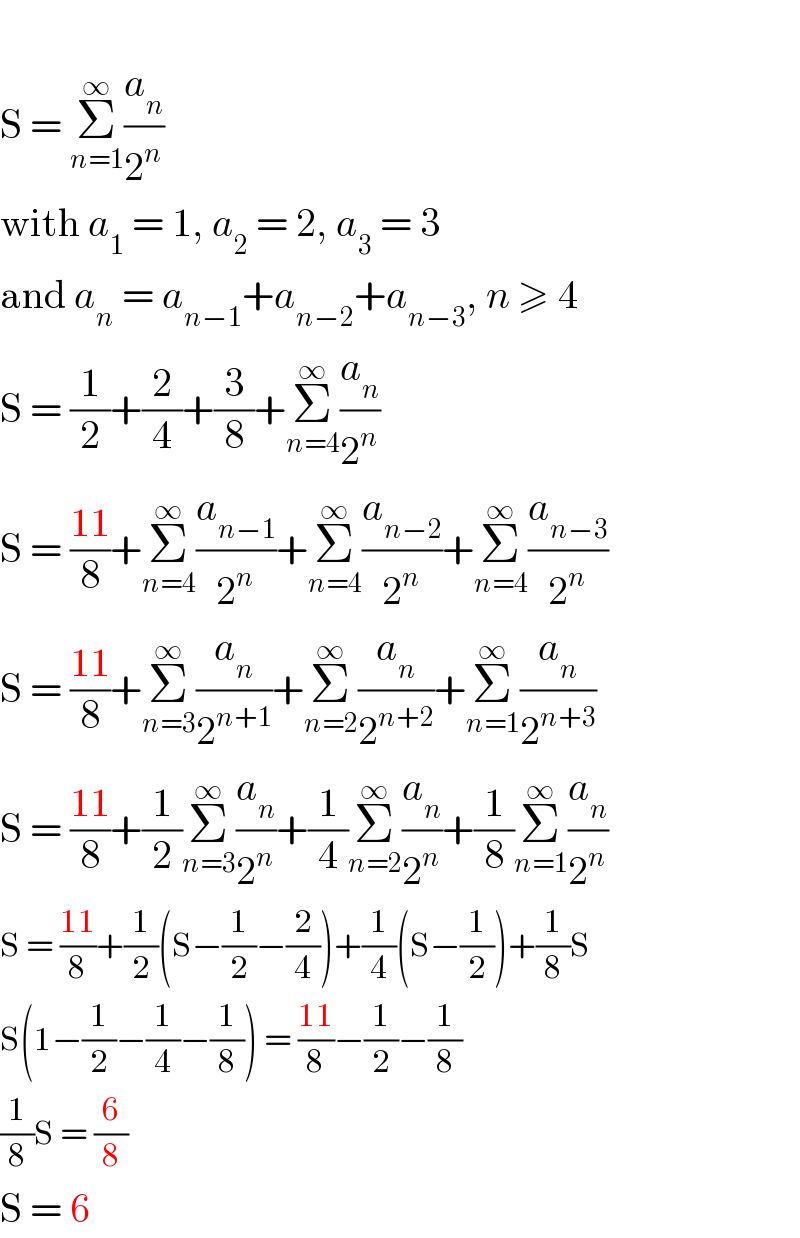
$$ \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{\mathrm{2}^{{n}} } \\ $$$$\mathrm{with}\:{a}_{\mathrm{1}} \:=\:\mathrm{1},\:{a}_{\mathrm{2}} \:=\:\mathrm{2},\:{a}_{\mathrm{3}} \:=\:\mathrm{3} \\ $$$$\mathrm{and}\:{a}_{{n}} \:=\:{a}_{{n}−\mathrm{1}} +{a}_{{n}−\mathrm{2}} +{a}_{{n}−\mathrm{3}} ,\:{n}\:\geqslant\:\mathrm{4} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{8}}+\underset{{n}=\mathrm{4}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{\mathrm{2}^{{n}} } \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{11}}{\mathrm{8}}+\underset{{n}=\mathrm{4}} {\overset{\infty} {\sum}}\frac{{a}_{{n}−\mathrm{1}} }{\mathrm{2}^{{n}} }+\underset{{n}=\mathrm{4}} {\overset{\infty} {\sum}}\frac{{a}_{{n}−\mathrm{2}} }{\mathrm{2}^{{n}} }+\underset{{n}=\mathrm{4}} {\overset{\infty} {\sum}}\frac{{a}_{{n}−\mathrm{3}} }{\mathrm{2}^{{n}} } \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{11}}{\mathrm{8}}+\underset{{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{\mathrm{2}^{{n}+\mathrm{1}} }+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{\mathrm{2}^{{n}+\mathrm{2}} }+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{\mathrm{2}^{{n}+\mathrm{3}} } \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{11}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{\mathrm{2}^{{n}} }+\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{\mathrm{2}^{{n}} }+\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{\mathrm{2}^{{n}} } \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{11}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{S}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{2}}{\mathrm{4}}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{S}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{S} \\ $$$$\mathrm{S}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}}\right)\:=\:\frac{\mathrm{11}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\frac{\mathrm{1}}{\mathrm{8}}\mathrm{S}\:=\:\frac{\mathrm{6}}{\mathrm{8}} \\ $$$$\mathrm{S}\:=\:\mathrm{6} \\ $$
Commented by prakash jain last updated on 29/Sep/20
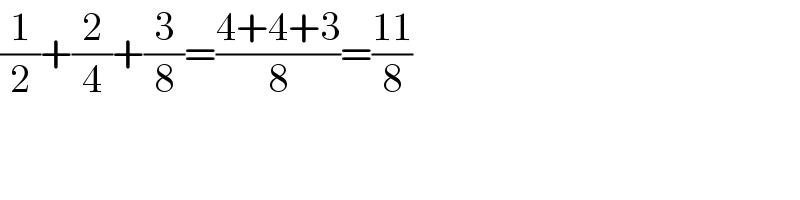
$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{8}}=\frac{\mathrm{4}+\mathrm{4}+\mathrm{3}}{\mathrm{8}}=\frac{\mathrm{11}}{\mathrm{8}} \\ $$
Commented by Olaf last updated on 29/Sep/20

$$\mathrm{Yes}\:!\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{mister}.\:\mathrm{I}\:\mathrm{corrected}. \\ $$
