Menu Close

Question-70497

Tinku Tara 0 Comments
Pin




Question Number 70497 by mr W last updated on 04/Oct/19
Commented by mr W last updated on 04/Oct/19
shaded area=?
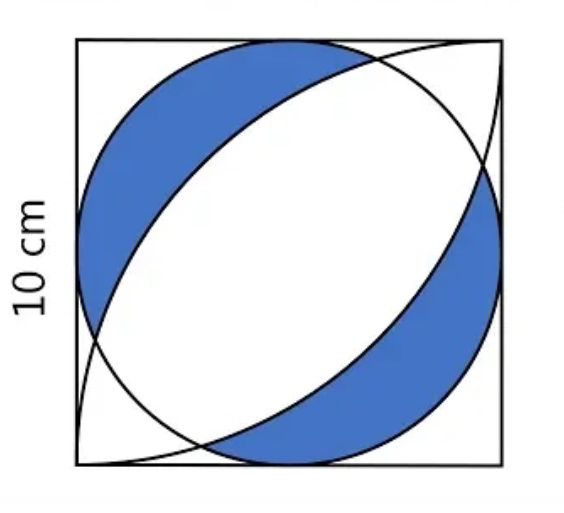
$${shaded}\:{area}=? \\ $$
Answered by ajfour last updated on 04/Oct/19
Commented by ajfour last updated on 04/Oct/19
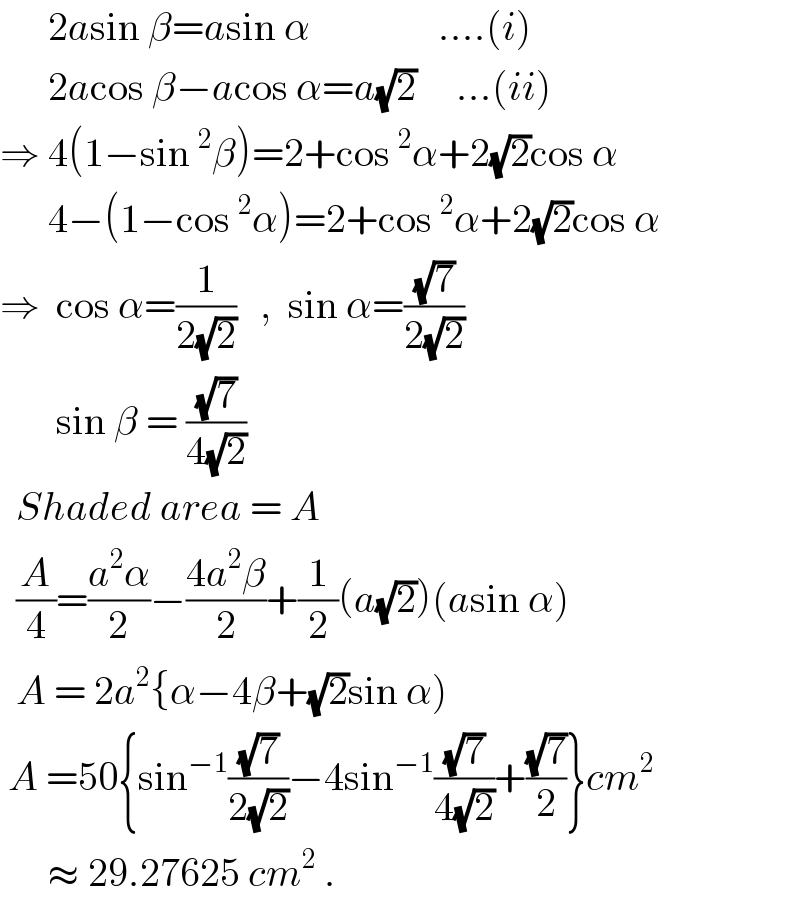
2asin β=asin α ....(i) 2acos β−acos α=a(√2) ...(ii) ⇒ 4(1−sin^2 β)=2+cos^2 α+2(√2)cos α 4−(1−cos^2 α)=2+cos^2 α+2(√2)cos α ⇒ cos α=(1/(2(√2))) , sin α=((√7)/(2(√2))) sin β = ((√7)/(4(√2))) Shaded area = A (A/4)=((a^2 α)/2)−((4a^2 β)/2)+(1/2)(a(√2))(asin α) A = 2a^2 {α−4β+(√2)sin α) A =50{sin^(−1) ((√7)/(2(√2)))−4sin^(−1) ((√7)/(4(√2)))+((√7)/2)}cm^2 ≈ 29.27625 cm^2 .
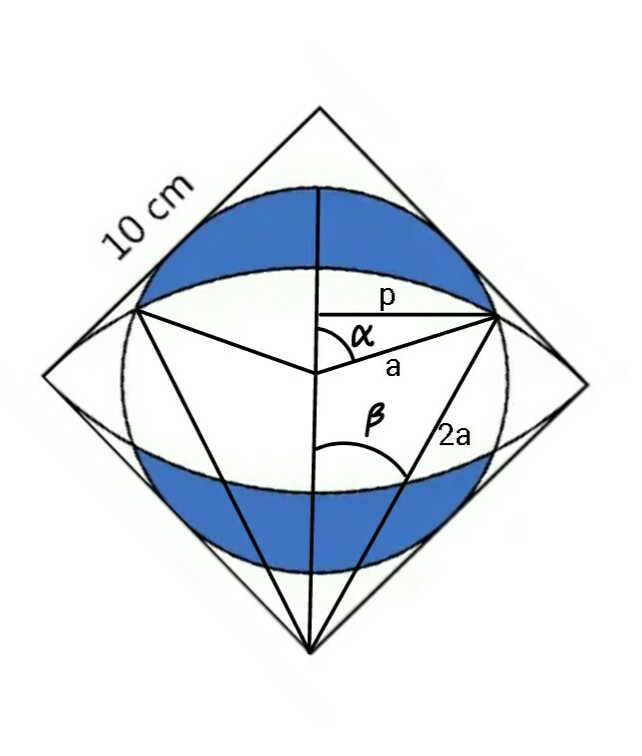
$$\:\:\:\:\:\:\mathrm{2}{a}\mathrm{sin}\:\beta={a}\mathrm{sin}\:\alpha\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left({i}\right) \\ $$$$\:\:\:\:\:\:\mathrm{2}{a}\mathrm{cos}\:\beta−{a}\mathrm{cos}\:\alpha={a}\sqrt{\mathrm{2}}\:\:\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\:\mathrm{4}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \beta\right)=\mathrm{2}+\mathrm{cos}\:^{\mathrm{2}} \alpha+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{cos}\:\alpha \\ $$$$\:\:\:\:\:\:\mathrm{4}−\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \alpha\right)=\mathrm{2}+\mathrm{cos}\:^{\mathrm{2}} \alpha+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\:\:,\:\:\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{7}}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\mathrm{sin}\:\beta\:=\:\frac{\sqrt{\mathrm{7}}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$$\:\:{Shaded}\:{area}\:=\:{A} \\ $$$$\:\:\frac{{A}}{\mathrm{4}}=\frac{{a}^{\mathrm{2}} \alpha}{\mathrm{2}}−\frac{\mathrm{4}{a}^{\mathrm{2}} \beta}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\left({a}\sqrt{\mathrm{2}}\right)\left({a}\mathrm{sin}\:\alpha\right) \\ $$$$\:\:{A}\:=\:\mathrm{2}{a}^{\mathrm{2}} \left\{\alpha−\mathrm{4}\beta+\sqrt{\mathrm{2}}\mathrm{sin}\:\alpha\right) \\ $$$$\:{A}\:=\mathrm{50}\left\{\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{7}}}{\mathrm{2}\sqrt{\mathrm{2}}}−\mathrm{4sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{7}}}{\mathrm{4}\sqrt{\mathrm{2}}}+\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right\}{cm}^{\mathrm{2}} \: \\ $$$$\:\:\:\:\:\:\approx\:\mathrm{29}.\mathrm{27625}\:{cm}^{\mathrm{2}} \:. \\ $$
Commented by mr W last updated on 05/Oct/19
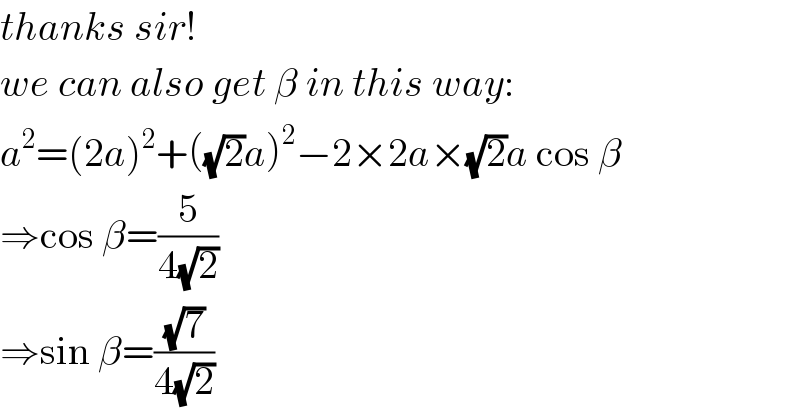
thanks sir! we can also get β in this way: a^2 =(2a)^2 +((√2)a)^2 −2×2a×(√2)a cos β ⇒cos β=(5/(4(√2))) ⇒sin β=((√7)/(4(√2)))
$${thanks}\:{sir}! \\ $$$${we}\:{can}\:{also}\:{get}\:\beta\:{in}\:{this}\:{way}: \\ $$$${a}^{\mathrm{2}} =\left(\mathrm{2}{a}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}{a}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{2}{a}×\sqrt{\mathrm{2}}{a}\:\mathrm{cos}\:\beta \\ $$$$\Rightarrow\mathrm{cos}\:\beta=\frac{\mathrm{5}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{sin}\:\beta=\frac{\sqrt{\mathrm{7}}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$
Commented by ajfour last updated on 05/Oct/19
Two roads diverged in a wood, I chose the one less traveled by..
$${Two}\:{roads}\:{diverged}\:{in}\:{a}\:{wood}, \\ $$$${I}\:{chose}\:{the}\:{one}\:{less}\:{traveled}\:{by}.. \\ $$
Commented by mr W last updated on 05/Oct/19
truely, all roads lead to Rome!
$${truely},\:{all}\:{roads}\:{lead}\:{to}\:{Rome}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *