Question Number 181618 by Mastermind last updated on 27/Nov/22
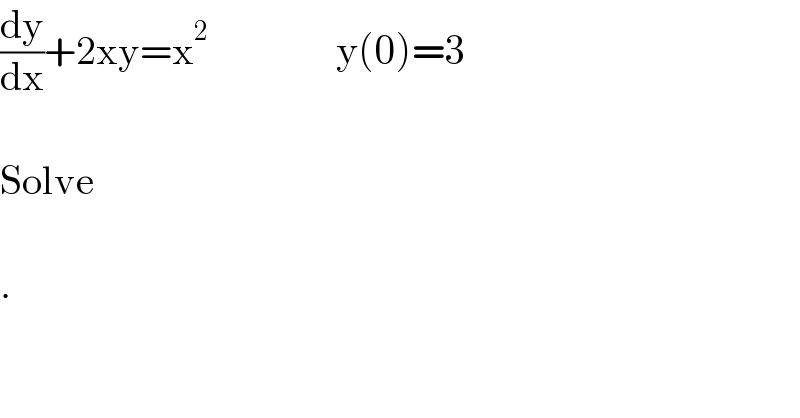
$$\frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{2xy}=\mathrm{x}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{y}\left(\mathrm{0}\right)=\mathrm{3} \\ $$$$ \\ $$$$\mathrm{Solve} \\ $$$$ \\ $$$$. \\ $$
Answered by hmr last updated on 27/Nov/22
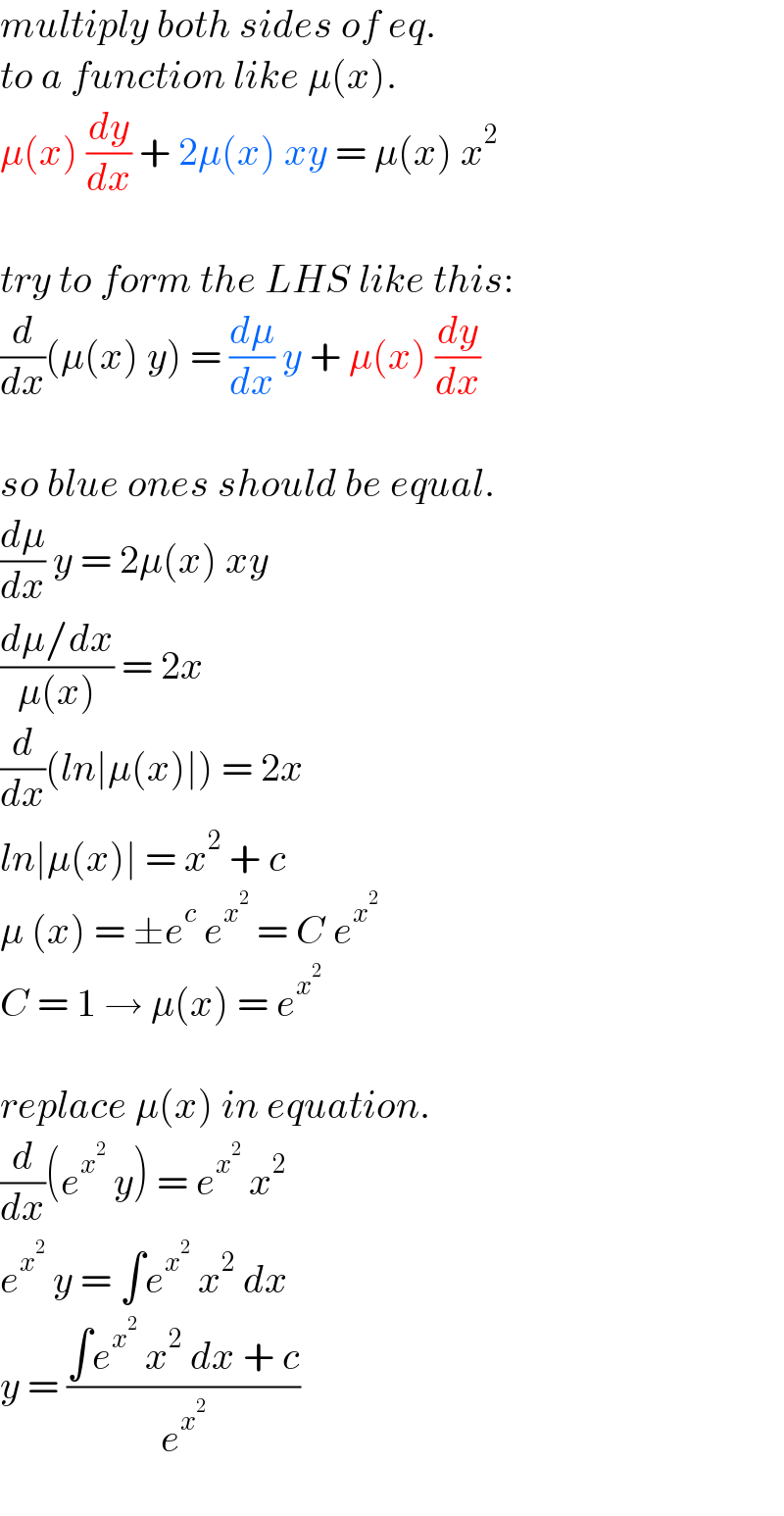
$${multiply}\:{both}\:{sides}\:{of}\:{eq}. \\ $$$${to}\:{a}\:{function}\:{like}\:\mu\left({x}\right). \\ $$$$\mu\left({x}\right)\:\frac{{dy}}{{dx}}\:+\:\mathrm{2}\mu\left({x}\right)\:{xy}\:=\:\mu\left({x}\right)\:{x}^{\mathrm{2}} \\ $$$$ \\ $$$${try}\:{to}\:{form}\:{the}\:{LHS}\:{like}\:{this}: \\ $$$$\frac{{d}}{{dx}}\left(\mu\left({x}\right)\:{y}\right)\:=\:\frac{{d}\mu}{{dx}}\:{y}\:+\:\mu\left({x}\right)\:\frac{{dy}}{{dx}}\: \\ $$$$ \\ $$$${so}\:{blue}\:{ones}\:{should}\:{be}\:{equal}. \\ $$$$\frac{{d}\mu}{{dx}}\:{y}\:=\:\mathrm{2}\mu\left({x}\right)\:{xy}\: \\ $$$$\frac{{d}\mu/{dx}}{\mu\left({x}\right)}\:=\:\mathrm{2}{x} \\ $$$$\frac{{d}}{{dx}}\left({ln}\mid\mu\left({x}\right)\mid\right)\:=\:\mathrm{2}{x} \\ $$$${ln}\mid\mu\left({x}\right)\mid\:=\:{x}^{\mathrm{2}} \:+\:{c} \\ $$$$\mu\:\left({x}\right)\:=\:\pm{e}^{{c}} \:{e}^{{x}^{\mathrm{2}} } \:=\:{C}\:{e}^{{x}^{\mathrm{2}} } \\ $$$${C}\:=\:\mathrm{1}\:\rightarrow\:\mu\left({x}\right)\:=\:{e}^{{x}^{\mathrm{2}} } \\ $$$$ \\ $$$${replace}\:\mu\left({x}\right)\:{in}\:{equation}. \\ $$$$\frac{{d}}{{dx}}\left({e}^{{x}^{\mathrm{2}} } \:{y}\right)\:=\:{e}^{{x}^{\mathrm{2}} } \:{x}^{\mathrm{2}} \\ $$$${e}^{{x}^{\mathrm{2}} } \:{y}\:=\:\int{e}^{{x}^{\mathrm{2}} } \:{x}^{\mathrm{2}} \:{dx} \\ $$$${y}\:=\:\frac{\int{e}^{{x}^{\mathrm{2}} } \:{x}^{\mathrm{2}} \:{dx}\:+\:{c}}{{e}^{{x}^{\mathrm{2}} } }\: \\ $$$$ \\ $$
Answered by ali009 last updated on 28/Nov/22
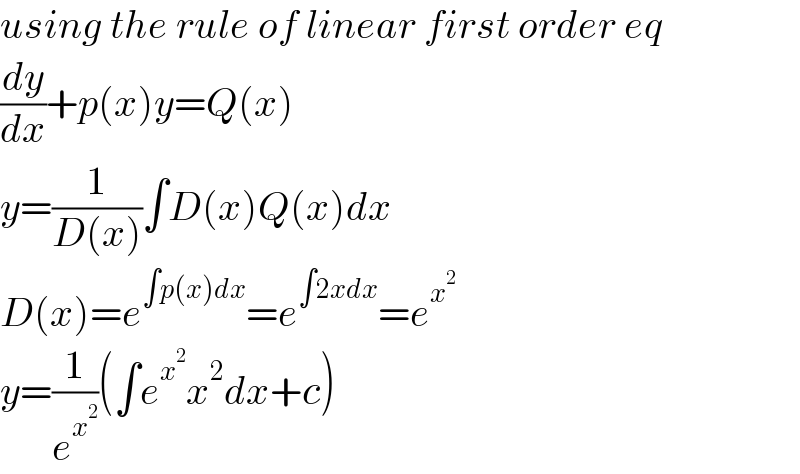
$${using}\:{the}\:{rule}\:{of}\:{linear}\:{first}\:{order}\:{eq} \\ $$$$\frac{{dy}}{{dx}}+{p}\left({x}\right){y}={Q}\left({x}\right) \\ $$$${y}=\frac{\mathrm{1}}{{D}\left({x}\right)}\int{D}\left({x}\right){Q}\left({x}\right){dx} \\ $$$${D}\left({x}\right)={e}^{\int{p}\left({x}\right){dx}} ={e}^{\int\mathrm{2}{xdx}} ={e}^{{x}^{\mathrm{2}} } \\ $$$${y}=\frac{\mathrm{1}}{{e}^{{x}^{\mathrm{2}} } }\left(\int{e}^{{x}^{\mathrm{2}} } {x}^{\mathrm{2}} {dx}+{c}\right) \\ $$
