Menu Close

prove-that-lim-x-1-1-3-1-5-1-2x-1-xln-x-ln-x-2e-2-

Tinku Tara 0 Comments
Pin




Question Number 181644 by mathlove last updated on 28/Nov/22
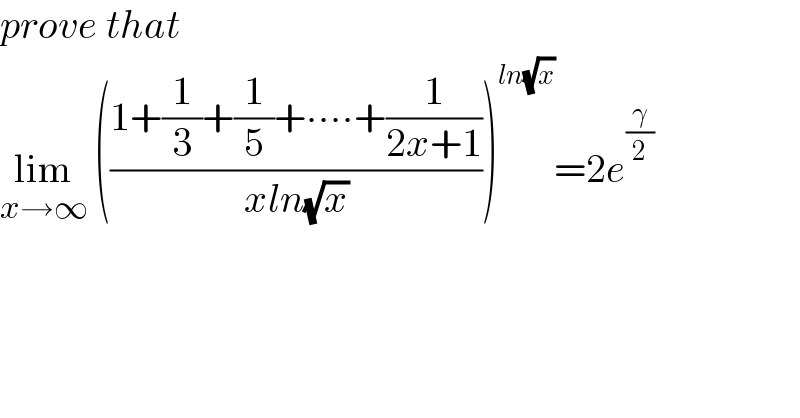
prove that lim_(x→∞) (((1+(1/3)+(1/5)+∙∙∙∙+(1/(2x+1)))/(xln(√x))))^(ln(√x)) =2e^(γ/2)
$${prove}\:{that} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+\centerdot\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}}{{xln}\sqrt{{x}}}\right)^{{ln}\sqrt{{x}}} =\mathrm{2}{e}^{\frac{\gamma}{\mathrm{2}}} \: \\ $$$$ \\ $$
Answered by aleks041103 last updated on 28/Nov/22
Answered by aleks041103 last updated on 28/Nov/22
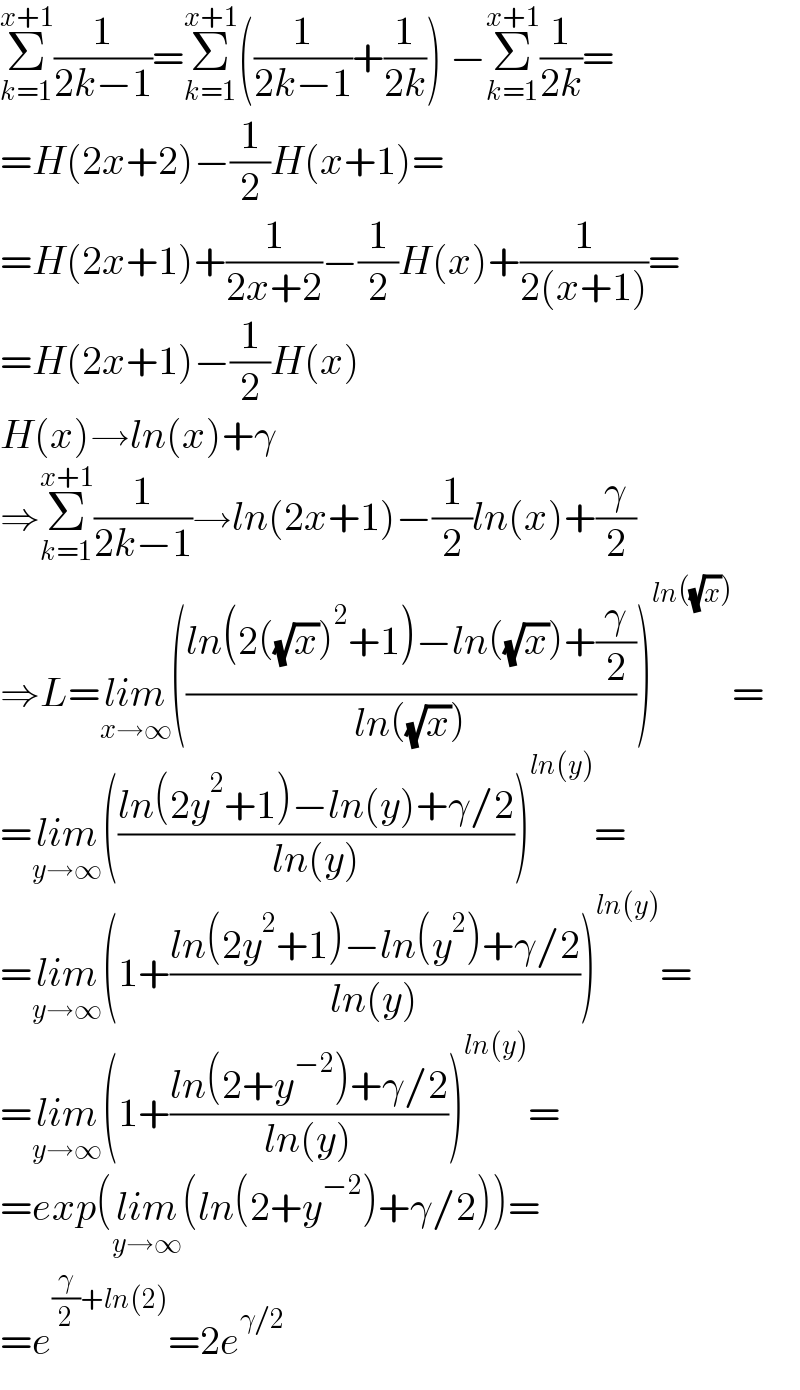
Σ_(k=1) ^(x+1) (1/(2k−1))=Σ_(k=1) ^(x+1) ((1/(2k−1))+(1/(2k))) −Σ_(k=1) ^(x+1) (1/(2k))= =H(2x+2)−(1/2)H(x+1)= =H(2x+1)+(1/(2x+2))−(1/2)H(x)+(1/(2(x+1)))= =H(2x+1)−(1/2)H(x) H(x)→ln(x)+γ ⇒Σ_(k=1) ^(x+1) (1/(2k−1))→ln(2x+1)−(1/2)ln(x)+(γ/2) ⇒L=lim_(x→∞) (((ln(2((√x))^2 +1)−ln((√x))+(γ/2))/(ln((√x)))))^(ln((√x))) = =lim_(y→∞) (((ln(2y^2 +1)−ln(y)+γ/2)/(ln(y))))^(ln(y)) = =lim_(y→∞) (1+((ln(2y^2 +1)−ln(y^2 )+γ/2)/(ln(y))))^(ln(y)) = =lim_(y→∞) (1+((ln(2+y^(−2) )+γ/2)/(ln(y))))^(ln(y)) = =exp(lim_(y→∞) (ln(2+y^(−2) )+γ/2))= =e^((γ/2)+ln(2)) =2e^(γ/2)
$$\underset{{k}=\mathrm{1}} {\overset{{x}+\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}=\underset{{k}=\mathrm{1}} {\overset{{x}+\mathrm{1}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}{k}}\right)\:−\underset{{k}=\mathrm{1}} {\overset{{x}+\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}}= \\ $$$$={H}\left(\mathrm{2}{x}+\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}{H}\left({x}+\mathrm{1}\right)= \\ $$$$={H}\left(\mathrm{2}{x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{H}\left({x}\right)+\frac{\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{1}\right)}= \\ $$$$={H}\left(\mathrm{2}{x}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}{H}\left({x}\right) \\ $$$${H}\left({x}\right)\rightarrow{ln}\left({x}\right)+\gamma \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{{x}+\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\rightarrow{ln}\left(\mathrm{2}{x}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}\right)+\frac{\gamma}{\mathrm{2}} \\ $$$$\Rightarrow{L}=\underset{{x}\rightarrow\infty} {{lim}}\left(\frac{{ln}\left(\mathrm{2}\left(\sqrt{{x}}\right)^{\mathrm{2}} +\mathrm{1}\right)−{ln}\left(\sqrt{{x}}\right)+\frac{\gamma}{\mathrm{2}}}{{ln}\left(\sqrt{{x}}\right)}\right)^{{ln}\left(\sqrt{{x}}\right)} = \\ $$$$=\underset{{y}\rightarrow\infty} {{lim}}\left(\frac{{ln}\left(\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}\right)−{ln}\left({y}\right)+\gamma/\mathrm{2}}{{ln}\left({y}\right)}\right)^{{ln}\left({y}\right)} = \\ $$$$=\underset{{y}\rightarrow\infty} {{lim}}\left(\mathrm{1}+\frac{{ln}\left(\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}\right)−{ln}\left({y}^{\mathrm{2}} \right)+\gamma/\mathrm{2}}{{ln}\left({y}\right)}\right)^{{ln}\left({y}\right)} = \\ $$$$=\underset{{y}\rightarrow\infty} {{lim}}\left(\mathrm{1}+\frac{{ln}\left(\mathrm{2}+{y}^{−\mathrm{2}} \right)+\gamma/\mathrm{2}}{{ln}\left({y}\right)}\right)^{{ln}\left({y}\right)} = \\ $$$$={exp}\left(\underset{{y}\rightarrow\infty} {{lim}}\left({ln}\left(\mathrm{2}+{y}^{−\mathrm{2}} \right)+\gamma/\mathrm{2}\right)\right)= \\ $$$$={e}^{\frac{\gamma}{\mathrm{2}}+{ln}\left(\mathrm{2}\right)} =\mathrm{2}{e}^{\gamma/\mathrm{2}} \\ $$
Commented by aleks041103 last updated on 28/Nov/22
Commented by mathlove last updated on 28/Nov/22
thanks
$${thanks} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *