Question Number 50732 by hassentimol last updated on 19/Dec/18

Answered by Rasheed.Sindhi last updated on 19/Dec/18
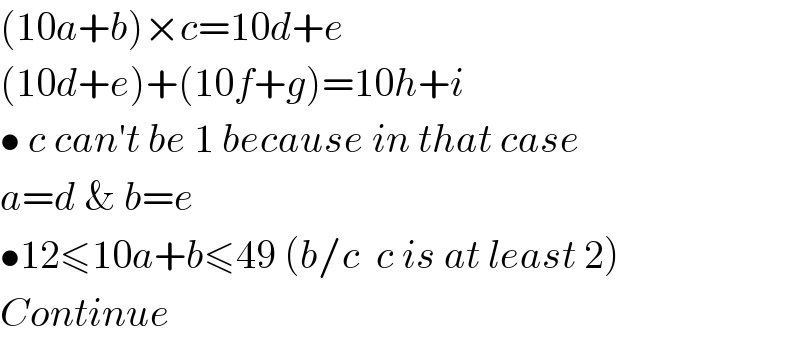
$$\left(\mathrm{10}{a}+{b}\right)×{c}=\mathrm{10}{d}+{e} \\ $$$$\left(\mathrm{10}{d}+{e}\right)+\left(\mathrm{10}{f}+{g}\right)=\mathrm{10}{h}+{i} \\ $$$$\bullet\:{c}\:{can}'{t}\:{be}\:\mathrm{1}\:{because}\:{in}\:{that}\:{case} \\ $$$${a}={d}\:\&\:{b}={e} \\ $$$$\bullet\mathrm{12}\leqslant\mathrm{10}{a}+{b}\leqslant\mathrm{49}\:\left({b}/{c}\:\:{c}\:{is}\:{at}\:{least}\:\mathrm{2}\right) \\ $$$${Continue} \\ $$
Commented by hassentimol last updated on 19/Dec/18

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by hassentimol last updated on 19/Dec/18

$$\mathrm{But}\:\mathrm{it}\:\mathrm{is}\:\mathrm{impossible}\:\mathrm{to}\:\mathrm{resolve}… \\ $$$$\mathrm{There}\:\mathrm{is}\:\mathrm{too}\:\mathrm{much}\:\mathrm{unknown}\:\mathrm{and}\:\mathrm{only} \\ $$$$\mathrm{2}\:\mathrm{equations}…\:? \\ $$
Answered by Rasheed.Sindhi last updated on 20/Dec/18

$$\:\:\:\:\:\mathrm{1}\:\:\mathrm{7} \\ $$$$×\:\:\:\:\mathrm{4} \\ $$$$−−−− \\ $$$$\:\:\:\:\:\mathrm{6}\:\:\mathrm{8} \\ $$$$+\:\mathrm{2}\:\:\mathrm{5} \\ $$$$−−−− \\ $$$$\:\:\:\:\mathrm{9}\:\:\:\mathrm{3} \\ $$
Commented by ajfour last updated on 20/Dec/18
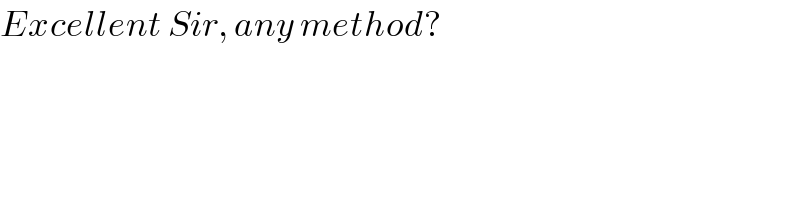
$${Excellent}\:{Sir},\:{any}\:{method}? \\ $$
Commented by Rasheed.Sindhi last updated on 20/Dec/18

$$\mathcal{T}{han}\Bbbk{s}\:{for}\:{encouraging}\:{Sir}! \\ $$$${The}\:{method}\:{is}\:{a}\:{mixture}\:{of}\:{intelligent} \\ $$$${guessing}\:\&\:{trial}. \\ $$
Answered by MJS last updated on 21/Dec/18

$${ab}×{c}={de} \\ $$$${b},{c}\:\neq\mathrm{1}\:\mathrm{otherwise}\:{e}={b}\vee{e}={c}\:\Rightarrow\:{c}\geqslant\mathrm{2} \\ $$$${de}<\mathrm{100}\wedge{c}\geqslant\mathrm{2}\:\Rightarrow\:{a}\leqslant\mathrm{4} \\ $$$${b},{c}\:\neq\mathrm{5}\:\mathrm{otherwise}\:{e}=\mathrm{5}\vee{e}=\mathrm{0} \\ $$$$\left({b},{c}\right)\notin\left\{\left(\mathrm{2},\mathrm{6}\right),\left(\mathrm{4},\mathrm{6}\right),\left(\mathrm{6},\mathrm{2}\right),\left(\mathrm{6},\mathrm{4}\right),\left(\mathrm{6},\mathrm{8}\right),\left(\mathrm{8},\mathrm{6}\right)\right\} \\ $$$$\mathrm{which}\:\mathrm{combinations}\:\mathrm{fit}? \\ $$$${c}=\mathrm{2}\wedge{a}=\mathrm{1}\:\Rightarrow\:{b}\in\left\{\mathrm{7},\mathrm{8},\mathrm{9}\right\} \\ $$$${c}=\mathrm{2}\wedge{a}=\mathrm{3}\:\Rightarrow\:{b}\in\left\{\mathrm{4},\mathrm{8},\mathrm{9}\right\} \\ $$$${c}=\mathrm{2}\wedge{a}=\mathrm{4}\:\Rightarrow\:{b}\in\left\{\mathrm{3},\mathrm{8}\right\} \\ $$$${c}=\mathrm{3}\wedge{a}=\mathrm{1}\:\Rightarrow\:{b}\in\left\{\mathrm{6},\mathrm{8},\mathrm{9}\right\} \\ $$$${c}=\mathrm{3}\wedge{a}=\mathrm{2}\:\Rightarrow\:{b}\in\left\{\mathrm{6},\mathrm{7},\mathrm{9}\right\} \\ $$$${c}=\mathrm{4}\wedge{a}=\mathrm{1}\:\Rightarrow\:{b}\in\left\{\mathrm{3},\mathrm{7},\mathrm{8},\mathrm{9}\right\} \\ $$$${c}=\mathrm{6}\wedge{a}=\mathrm{1}\:\Rightarrow\:{b}=\mathrm{3} \\ $$$${c}=\mathrm{7}\wedge{a}=\mathrm{1}\:\Rightarrow\:{b}\in\left\{\mathrm{2},\mathrm{4}\right\} \\ $$$${c}=\mathrm{8}\wedge{a}=\mathrm{1}\:\Rightarrow\:{b}=\mathrm{2} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{have}: \\ $$$$\left(\mathrm{1}\right)\:\mathrm{listed}\:{c}×{de}={fg} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{wrote}\:\mathrm{down}\:\mathrm{left}\:\mathrm{digits}\:\mathrm{in}\:\left\{\right\} \\ $$$$\left(\mathrm{3}\right)\:“{X}''\:\mathrm{sorted}\:\mathrm{out}\:\mathrm{because}\:\mathrm{no}\:\mathrm{possibility}\:\mathrm{to}\:\mathrm{add} \\ $$$$\mathrm{a}\:\mathrm{2}\:\mathrm{digit}\:\mathrm{number}\:\mathrm{and}\:\mathrm{stay}\:<\mathrm{100} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{testing}\:\mathrm{the}\:\mathrm{matches}\:\mathrm{for}\:{de}+{fg}={hi} \\ $$$$\mathrm{2}×\mathrm{17}=\mathrm{34}\:\left\{\mathrm{5},\mathrm{6},\mathrm{8},\mathrm{9}\right\}\:\mathrm{34}+{f}\mathrm{5}={h}\mathrm{9}\:{X} \\ $$$$\mathrm{2}×\mathrm{18}=\mathrm{36}\:\left\{\mathrm{4},\mathrm{5},\mathrm{7},\mathrm{9}\right\}\:\mathrm{36}+{f}\mathrm{9}={h}\mathrm{5}\:{X} \\ $$$$\mathrm{2}×\mathrm{19}=\mathrm{38}\:\left\{\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{7}\right\}\:\mathrm{38}+{f}\mathrm{6}={h}\mathrm{4}\:{X}\:\mathrm{38}+{f}\mathrm{7}={h}\mathrm{5}\:{X} \\ $$$$\mathrm{2}×\mathrm{34}=\mathrm{68}\:\left\{\mathrm{1},\mathrm{5},\mathrm{7},\mathrm{9}\right\}\:\mathrm{68}+{f}\mathrm{1}={g}\mathrm{9}\:{X}\:\mathrm{68}+{f}\mathrm{7}={h}\mathrm{5}\:{X}\:\mathrm{68}+{f}\mathrm{9}={h}\mathrm{7}\:{X} \\ $$$$\mathrm{2}×\mathrm{38}=\mathrm{76}\:\left\{\mathrm{1},\mathrm{4},\mathrm{5},\mathrm{9}\right\}\:\mathrm{76}+{f}\mathrm{5}={h}\mathrm{1}\:{X}\:\mathrm{76}+{f}\mathrm{9}={h}\mathrm{5}\:{X} \\ $$$$\mathrm{2}×\mathrm{39}=\mathrm{78}\:\left\{\mathrm{1},\mathrm{4},\mathrm{5},\mathrm{6}\right\}\:\mathrm{78}+{f}\mathrm{6}={h}\mathrm{4}\:{X} \\ $$$$\mathrm{2}×\mathrm{43}=\mathrm{86}\:\left\{\mathrm{1},\mathrm{5},\mathrm{7},\mathrm{9}\right\}\:{X} \\ $$$$\mathrm{2}×\mathrm{48}=\mathrm{96}\:\left\{\mathrm{1},\mathrm{3},\mathrm{5},\mathrm{7}\right\}\:{X} \\ $$$$\mathrm{3}×\mathrm{16}=\mathrm{48}\:\left\{\mathrm{2},\mathrm{5},\mathrm{7},\mathrm{9}\right\}\:\mathrm{48}+{f}\mathrm{7}={h}\mathrm{5}\:{X}\:\mathrm{48}+{f}\mathrm{9}={h}\mathrm{7}\:{X} \\ $$$$\mathrm{3}×\mathrm{18}=\mathrm{54}\:\left\{\mathrm{2},\mathrm{6},\mathrm{7},\mathrm{9}\right\}\:\mathrm{54}+{f}\mathrm{2}={h}\mathrm{6}\:{X} \\ $$$$\mathrm{3}×\mathrm{19}=\mathrm{57}\:\left\{\mathrm{2},\mathrm{4},\mathrm{6},\mathrm{8}\right\}\:{X} \\ $$$$\mathrm{3}×\mathrm{26}=\mathrm{78}\:\left\{\mathrm{1},\mathrm{4},\mathrm{5},\mathrm{9}\right\}\:\mathrm{78}+{f}\mathrm{1}={h}\mathrm{9}\:{X} \\ $$$$\mathrm{3}×\mathrm{27}=\mathrm{81}\:\left\{\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{9}\right\}\:{X} \\ $$$$\mathrm{3}×\mathrm{29}=\mathrm{87}\:\left\{\mathrm{1},\mathrm{4},\mathrm{5},\mathrm{6}\right\}\:{X} \\ $$$$\mathrm{4}×\mathrm{13}=\mathrm{52}\:\left\{\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9}\right\}\:{X} \\ $$$$\mathrm{4}×\mathrm{17}=\mathrm{68}\:\left\{\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{9}\right\}\:\mathrm{68}+{f}\mathrm{5}={h}\mathrm{3}\:\Rightarrow\:\mathrm{68}+\mathrm{25}=\mathrm{93} \\ $$$$\mathrm{4}×\mathrm{18}=\mathrm{72}\:\left\{\mathrm{3},\mathrm{5},\mathrm{6},\mathrm{9}\right\}\:{X} \\ $$$$\mathrm{4}×\mathrm{19}=\mathrm{76}\:\left\{\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{8}\right\}\:\mathrm{76}+{f}\mathrm{2}={h}\mathrm{8}\:{X} \\ $$$$\mathrm{6}×\mathrm{13}=\mathrm{78}\:\left\{\mathrm{2},\mathrm{4},\mathrm{5},\mathrm{9}\right\}\:{X} \\ $$$$\mathrm{7}×\mathrm{12}=\mathrm{84}\:\left\{\mathrm{3},\mathrm{5},\mathrm{6},\mathrm{9}\right\}\:{X} \\ $$$$\mathrm{7}×\mathrm{14}=\mathrm{98}\:\left\{\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{6}\right\}\:{X} \\ $$$$\mathrm{8}×\mathrm{12}=\mathrm{96}\:\left\{\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{7}\right\}\:{X} \\ $$
Commented by Rasheed.Sindhi last updated on 03/Feb/19
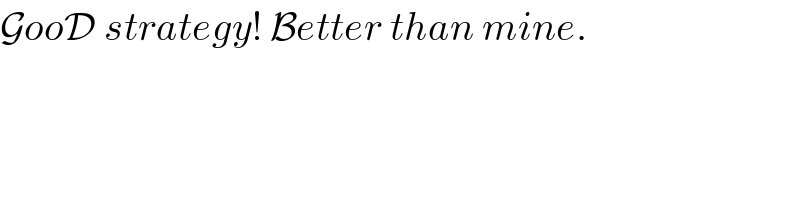
$$\mathcal{G}{oo}\mathcal{D}\:{strategy}!\:\mathcal{B}{etter}\:{than}\:{mine}. \\ $$
Commented by hassentimol last updated on 24/Dec/18
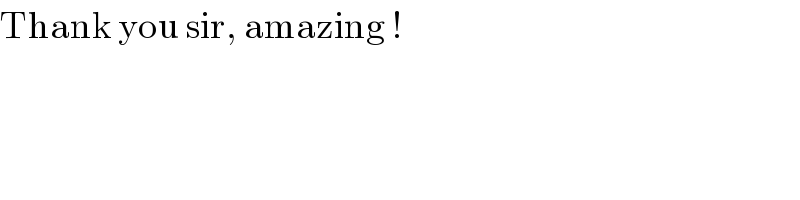
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{amazing}\:! \\ $$
