Question Number 65945 by Chi Mes Try last updated on 06/Aug/19

$${pls}\:{i}\:{need}\:{solution}\:{plssss}…{asap} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{n} \\ $$$$\:\:\:{lim}\:\:\:\:\:\:\:\:\:\:\:\in\:\:\:\:\left(\frac{{r}^{\mathrm{3}} }{{r}^{\mathrm{4}} +{n}^{\mathrm{4}} }\right) \\ $$$${n}\rightarrow\infty\:\:\:\:\:\:{r}=\mathrm{1} \\ $$$$ \\ $$$${please}\:{try}\:{and}\:{understand}\:{the}\:{way}\:{i}\:{typed}\:{it} \\ $$
Commented by MJS last updated on 06/Aug/19
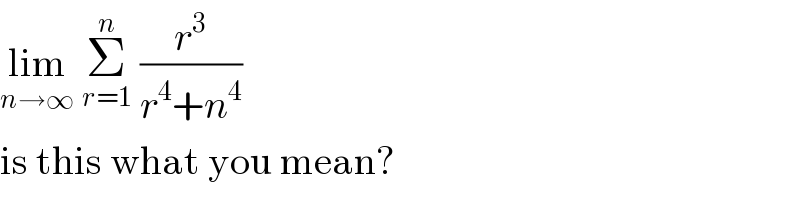
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{{r}^{\mathrm{3}} }{{r}^{\mathrm{4}} +{n}^{\mathrm{4}} } \\ $$$$\mathrm{is}\:\mathrm{this}\:\mathrm{what}\:\mathrm{you}\:\mathrm{mean}? \\ $$
Commented by mathmax by abdo last updated on 06/Aug/19
![let S_n =Σ_(k=1) ^n (k^3 /(n^4 +k^4 )) ⇒S_n =Σ_(k=1) ^n (1/n) × ((((k/n))^3 )/(1+((k/n))^4 )) so S_n is Rieman sum and lim_(n→+∞) S_n =∫_0 ^1 (x^3 /(1+x^4 ))dx =[(1/4)ln(1+x^4 )]_0 ^1 =((ln(2))/4)](https://www.tinkutara.com/question/Q65954.png)
$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}^{\mathrm{3}} }{{n}^{\mathrm{4}} \:+{k}^{\mathrm{4}} }\:\Rightarrow{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{n}}\:×\:\:\frac{\left(\frac{{k}}{{n}}\right)^{\mathrm{3}} }{\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{4}} } \\ $$$${so}\:{S}_{{n}} {is}\:{Rieman}\:{sum}\:{and}\:{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{4}} }{dx} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}+{x}^{\mathrm{4}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$
