Question Number 116318 by Bird last updated on 03/Oct/20
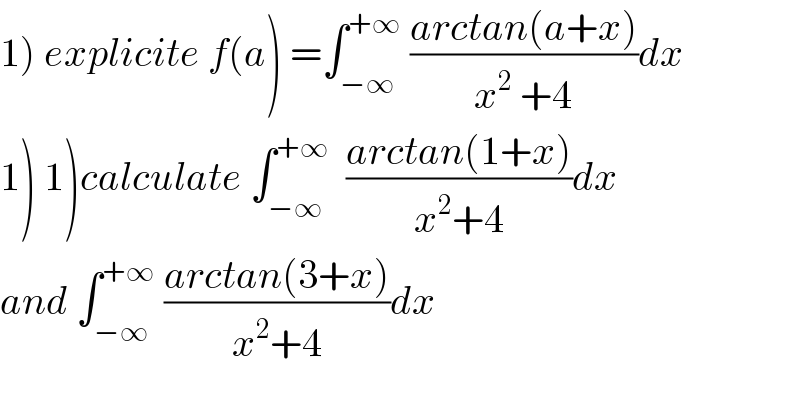
$$\left.\mathrm{1}\right)\:{explicite}\:{f}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\frac{{arctan}\left({a}+{x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx} \\ $$$$\left.\mathrm{1}\left.\right)\:\mathrm{1}\right){calculate}\:\int_{−\infty} ^{+\infty} \:\:\frac{{arctan}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} +\mathrm{4}}{dx} \\ $$$${and}\:\int_{−\infty} ^{+\infty} \:\frac{{arctan}\left(\mathrm{3}+{x}\right)}{{x}^{\mathrm{2}} +\mathrm{4}}{dx} \\ $$
Answered by Olaf last updated on 03/Oct/20
![1) F(x) = ∫_a ^b f(x,t)dt ⇒ F′(x) = ∫_a ^b (∂f/∂x)(x,t)dt Here we have : f′(a) = ∫_(−∞) ^(+∞) (1/(x^2 +4))×(1/((a+x)^2 +1))dx f′(a) = ∫_(−∞) ^(+∞) [((Ax+B)/(x^2 +4))+((C(x+a)+D)/((x+a)^2 +1))]dx A = −((2a)/((a^2 +1)(a^2 +9))) B = ((a^2 −3)/((a^2 +1)(a^2 +9))) C = ((2a)/((a^2 +1)(a^2 +9))) = −A D = ((a^2 +3)/((a^2 +1)(a^2 +9))) f′(a) = (A/2)[ln∣((x^2 +4)/((x+a)^2 +1))∣]_(−∞) ^(+∞) +(B/2)[arctan((x/2))]_(−∞) ^(+∞) +D[arctan(x+a)]_(−∞) ^(+∞) f′(a) = (π/2)B+πD f′(a) = ((3π)/2).(1/(a^2 +9)) ⇒ f(a) = (π/2)arctan(a/3)+K lim_(a→+∞) f(a) = (π^2 /4)+K and lim_(a→+∞) f(a) = ∫_(−∞) ^(+∞) (π/2).(1/(x^2 +4))dx lim_(a→+∞) f(a) = (π/4)[arctan(x/2)]_(−∞) ^(+∞) = (π^2 /4) ⇒ (π^2 /4)+K = (π^2 /4), K = 0 Finally f(a) = (π/2)arctan(a/3) 1)1) ∫_(−∞) ^(+∞) ((arctan(1+x))/(x^2 +4))dx = f(1) = (π/2)arctan(1/3) (arctan(1/3) = 0,322...) ∫_(−∞) ^(+∞) ((arctan(3+x))/(x^2 +4))dx = f(3) = (π/2)arctan(1) ∫_(−∞) ^(+∞) ((arctan(3+x))/(x^2 +4))dx = f(3) = (π^2 /8) Please verify my calculous...](https://www.tinkutara.com/question/Q116340.png)
$$\left.\mathrm{1}\right) \\ $$$$\mathrm{F}\left({x}\right)\:=\:\int_{{a}} ^{{b}} {f}\left({x},{t}\right){dt}\:\Rightarrow\:\mathrm{F}'\left({x}\right)\:=\:\int_{{a}} ^{{b}} \frac{\partial{f}}{\partial{x}}\left({x},{t}\right){dt} \\ $$$$\mathrm{Here}\:\mathrm{we}\:\mathrm{have}\:: \\ $$$${f}'\left({a}\right)\:=\:\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{4}}×\frac{\mathrm{1}}{\left({a}+{x}\right)^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$${f}'\left({a}\right)\:=\:\int_{−\infty} ^{+\infty} \left[\frac{\mathrm{A}{x}+\mathrm{B}}{{x}^{\mathrm{2}} +\mathrm{4}}+\frac{\mathrm{C}\left({x}+{a}\right)+\mathrm{D}}{\left({x}+{a}\right)^{\mathrm{2}} +\mathrm{1}}\right]{dx} \\ $$$$\mathrm{A}\:=\:−\frac{\mathrm{2}{a}}{\left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({a}^{\mathrm{2}} +\mathrm{9}\right)} \\ $$$$\mathrm{B}\:=\:\frac{{a}^{\mathrm{2}} −\mathrm{3}}{\left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({a}^{\mathrm{2}} +\mathrm{9}\right)} \\ $$$$\mathrm{C}\:=\:\frac{\mathrm{2}{a}}{\left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({a}^{\mathrm{2}} +\mathrm{9}\right)}\:=\:−\mathrm{A} \\ $$$$\mathrm{D}\:=\:\frac{{a}^{\mathrm{2}} +\mathrm{3}}{\left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({a}^{\mathrm{2}} +\mathrm{9}\right)} \\ $$$${f}'\left({a}\right)\:=\:\frac{\mathrm{A}}{\mathrm{2}}\left[\mathrm{ln}\mid\frac{{x}^{\mathrm{2}} +\mathrm{4}}{\left({x}+{a}\right)^{\mathrm{2}} +\mathrm{1}}\mid\right]_{−\infty} ^{+\infty} \\ $$$$+\frac{\mathrm{B}}{\mathrm{2}}\left[\mathrm{arctan}\left(\frac{{x}}{\mathrm{2}}\right)\right]_{−\infty} ^{+\infty} +\mathrm{D}\left[\mathrm{arctan}\left({x}+{a}\right)\right]_{−\infty} ^{+\infty} \\ $$$${f}'\left({a}\right)\:=\:\frac{\pi}{\mathrm{2}}\mathrm{B}+\pi\mathrm{D} \\ $$$${f}'\left({a}\right)\:=\:\frac{\mathrm{3}\pi}{\mathrm{2}}.\frac{\mathrm{1}}{{a}^{\mathrm{2}} +\mathrm{9}} \\ $$$$\Rightarrow\:{f}\left({a}\right)\:=\:\frac{\pi}{\mathrm{2}}\mathrm{arctan}\frac{{a}}{\mathrm{3}}+\mathrm{K} \\ $$$$\underset{{a}\rightarrow+\infty} {\mathrm{lim}}{f}\left({a}\right)\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}}+\mathrm{K} \\ $$$$\mathrm{and}\:\underset{{a}\rightarrow+\infty} {\mathrm{lim}}{f}\left({a}\right)\:=\:\int_{−\infty} ^{+\infty} \frac{\pi}{\mathrm{2}}.\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx} \\ $$$$\underset{{a}\rightarrow+\infty} {\mathrm{lim}}{f}\left({a}\right)\:=\:\frac{\pi}{\mathrm{4}}\left[\mathrm{arctan}\frac{{x}}{\mathrm{2}}\right]_{−\infty} ^{+\infty} \:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}}+\mathrm{K}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}},\:\mathrm{K}\:=\:\mathrm{0} \\ $$$$\mathrm{Finally}\:{f}\left({a}\right)\:=\:\frac{\pi}{\mathrm{2}}\mathrm{arctan}\frac{{a}}{\mathrm{3}} \\ $$$$\left.\mathrm{1}\left.\right)\mathrm{1}\right) \\ $$$$\int_{−\infty} ^{+\infty} \frac{\mathrm{arctan}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}\:=\:{f}\left(\mathrm{1}\right)\:=\:\frac{\pi}{\mathrm{2}}\mathrm{arctan}\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left(\mathrm{arctan}\frac{\mathrm{1}}{\mathrm{3}}\:=\:\mathrm{0},\mathrm{322}…\right) \\ $$$$ \\ $$$$\int_{−\infty} ^{+\infty} \frac{\mathrm{arctan}\left(\mathrm{3}+{x}\right)}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}\:=\:{f}\left(\mathrm{3}\right)\:=\:\frac{\pi}{\mathrm{2}}\mathrm{arctan}\left(\mathrm{1}\right) \\ $$$$\int_{−\infty} ^{+\infty} \frac{\mathrm{arctan}\left(\mathrm{3}+{x}\right)}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}\:=\:{f}\left(\mathrm{3}\right)\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{Please}}\:\boldsymbol{\mathrm{verify}}\:\boldsymbol{\mathrm{my}}\:\boldsymbol{\mathrm{calculous}}… \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 03/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
