Question Number 116360 by bemath last updated on 03/Oct/20

$$\mathrm{A}\:\mathrm{five}\:\mathrm{digits}\:\mathrm{number}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{3} \\ $$$$\mathrm{is}\:\mathrm{to}\:\mathrm{be}\:\mathrm{formed}\:\mathrm{using}\:\mathrm{the}\:\mathrm{number}\: \\ $$$$\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\:\mathrm{and}\:\mathrm{5}\:\mathrm{without}\:\mathrm{repetition} \\ $$$$\mathrm{The}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{this}\:\mathrm{can} \\ $$$$\mathrm{be}\:\mathrm{done}\:\mathrm{is}\:\_\_ \\ $$
Answered by mr W last updated on 03/Oct/20
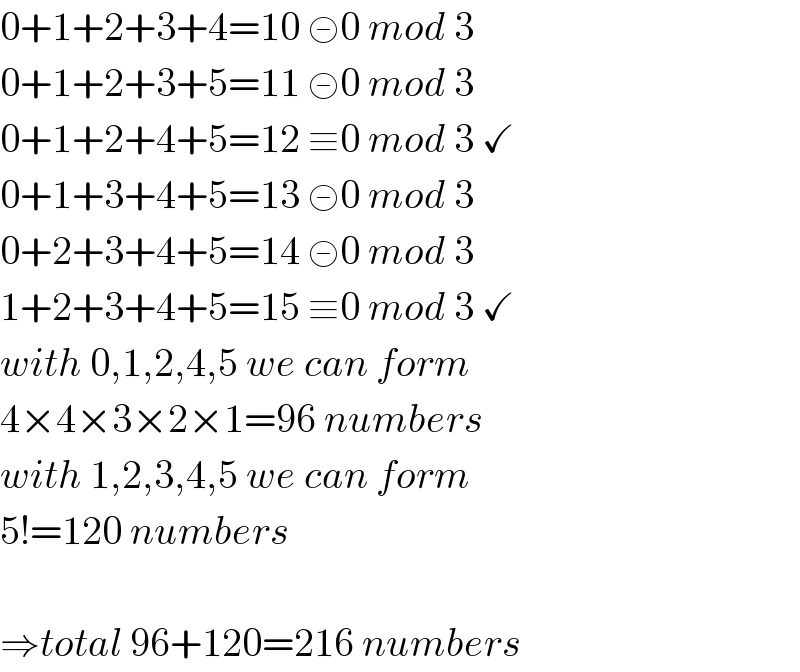
$$\mathrm{0}+\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}=\mathrm{10}\:≢\mathrm{0}\:{mod}\:\mathrm{3} \\ $$$$\mathrm{0}+\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{5}=\mathrm{11}\:≢\mathrm{0}\:{mod}\:\mathrm{3} \\ $$$$\mathrm{0}+\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{5}=\mathrm{12}\:\equiv\mathrm{0}\:{mod}\:\mathrm{3}\:\checkmark \\ $$$$\mathrm{0}+\mathrm{1}+\mathrm{3}+\mathrm{4}+\mathrm{5}=\mathrm{13}\:≢\mathrm{0}\:{mod}\:\mathrm{3} \\ $$$$\mathrm{0}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}=\mathrm{14}\:≢\mathrm{0}\:{mod}\:\mathrm{3} \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}=\mathrm{15}\:\equiv\mathrm{0}\:{mod}\:\mathrm{3}\:\checkmark \\ $$$${with}\:\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{4},\mathrm{5}\:{we}\:{can}\:{form} \\ $$$$\mathrm{4}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}=\mathrm{96}\:{numbers} \\ $$$${with}\:\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5}\:{we}\:{can}\:{form} \\ $$$$\mathrm{5}!=\mathrm{120}\:{numbers} \\ $$$$ \\ $$$$\Rightarrow{total}\:\mathrm{96}+\mathrm{120}=\mathrm{216}\:{numbers} \\ $$
