Question Number 50861 by majidedalt last updated on 21/Dec/18

$$\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{5}\right)!}=\mathrm{20}\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{3}\right)!} \\ $$$$ \\ $$$$\mathrm{n}=? \\ $$$$\_\_\_\_\_\_\_\_ \\ $$$$\mathrm{please}\:\mathrm{give}\:\mathrm{me}\:\mathrm{simple}\:\mathrm{solve}. \\ $$$$\mathrm{thanks} \\ $$
Answered by afachri last updated on 21/Dec/18

$$\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)\left({n}−\mathrm{3}\right)\left({n}−\mathrm{4}\right)\left({n}−\mathrm{5}\right)!}{\left({n}−\mathrm{5}\right)!}\:\:=\:\:\frac{\mathrm{20}.{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)\left({n}−\mathrm{3}\right)!}{\left({n}−\mathrm{3}\right)!} \\ $$$$\:\:\:\:\:\:\:{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)\left({n}−\mathrm{3}\right)\left({n}−\mathrm{4}\right)\:\:=\:\:\mathrm{20}\:{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left({n}−\mathrm{3}\right)\left({n}−\mathrm{4}\right)\:=\:\:\mathrm{20} \\ $$$$\:\:\:\:\:\:{n}^{\mathrm{2}} −\mathrm{7}{n}+\mathrm{12}−\mathrm{20}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{n}^{\mathrm{2}} −\mathrm{7}{n}−\mathrm{8}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left({n}−\mathrm{8}\right)\left({n}+\mathrm{1}\right)\:\:=\:\:\mathrm{0} \\ $$$${n}_{\mathrm{1}} =\:\mathrm{8}\:\:\:\:\:\:\:\:\mathrm{and}\:\:\:\:\:\:\:\:{n}_{\mathrm{2}} =\:−\mathrm{1} \\ $$$$\mathrm{since}\:\mathrm{factorial}\:\mathrm{is}\:\mathrm{possitive}\:\mathrm{function},\:\mathrm{the} \\ $$$$\mathrm{solution}\:\mathrm{is}\:\mathrm{only}\:{n}\:=\:\mathrm{8}. \\ $$$$ \\ $$
Commented by majidedalt last updated on 21/Dec/18

$$\mathrm{thanks}\:\mathrm{dear} \\ $$
Answered by afachri last updated on 21/Dec/18
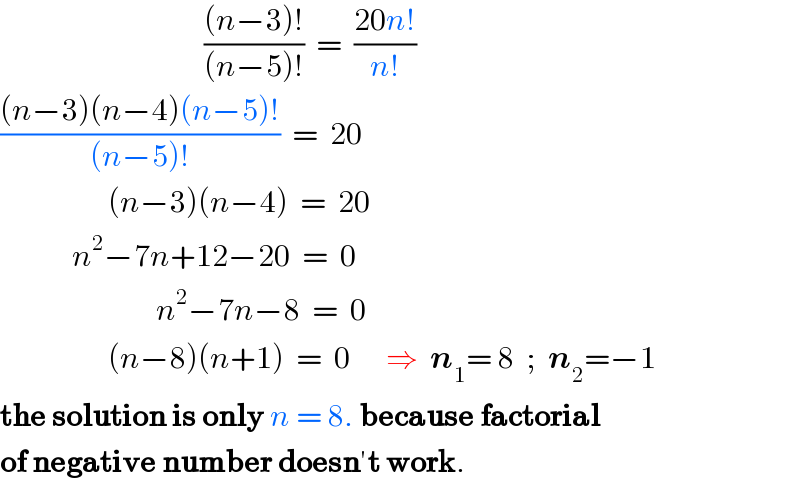
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\left({n}−\mathrm{3}\right)!}{\left({n}−\mathrm{5}\right)!}\:\:=\:\:\frac{\mathrm{20}{n}!}{{n}!} \\ $$$$\frac{\left({n}−\mathrm{3}\right)\left({n}−\mathrm{4}\right)\left({n}−\mathrm{5}\right)!}{\left({n}−\mathrm{5}\right)!}\:\:=\:\:\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({n}−\mathrm{3}\right)\left({n}−\mathrm{4}\right)\:\:=\:\:\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{n}^{\mathrm{2}} −\mathrm{7}{n}+\mathrm{12}−\mathrm{20}\:\:=\:\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{n}^{\mathrm{2}} −\mathrm{7}{n}−\mathrm{8}\:\:=\:\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({n}−\mathrm{8}\right)\left({n}+\mathrm{1}\right)\:\:=\:\:\mathrm{0}\:\:\:\:\:\:\Rightarrow\:\:\boldsymbol{{n}}_{\mathrm{1}} =\:\mathrm{8}\:\:;\:\:\boldsymbol{{n}}_{\mathrm{2}} =−\mathrm{1} \\ $$$$\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{only}}\:{n}\:=\:\mathrm{8}.\:\boldsymbol{\mathrm{because}}\:\boldsymbol{\mathrm{factorial}} \\ $$$$\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{negative}}\:\boldsymbol{\mathrm{number}}\:\boldsymbol{\mathrm{doesn}}'\boldsymbol{\mathrm{t}}\:\boldsymbol{\mathrm{work}}. \\ $$
Commented by majidedalt last updated on 21/Dec/18

$$\mathrm{very}\:\mathrm{thanks} \\ $$
