Question Number 116480 by Dwaipayan Shikari last updated on 04/Oct/20
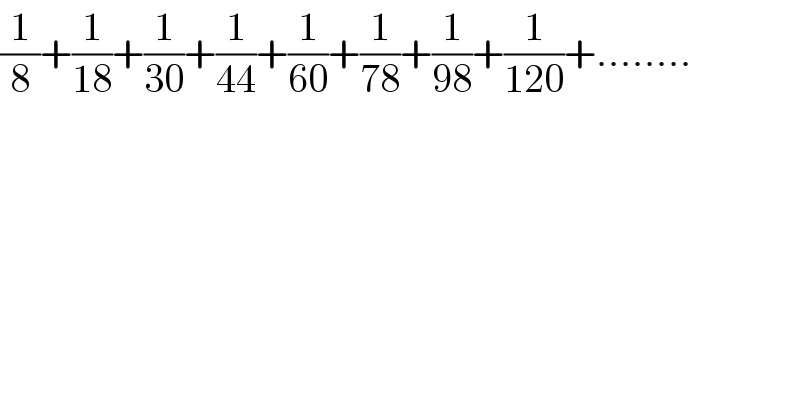
$$\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{18}}+\frac{\mathrm{1}}{\mathrm{30}}+\frac{\mathrm{1}}{\mathrm{44}}+\frac{\mathrm{1}}{\mathrm{60}}+\frac{\mathrm{1}}{\mathrm{78}}+\frac{\mathrm{1}}{\mathrm{98}}+\frac{\mathrm{1}}{\mathrm{120}}+…….. \\ $$
Answered by Olaf last updated on 04/Oct/20

$${u}_{{n}} \:=\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{7}{n}}\:=\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{7}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{7}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{7}}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{u}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{7}}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{7}}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{u}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{7}}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\underset{{n}=\mathrm{8}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{u}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{7}}\underset{{n}=\mathrm{1}} {\overset{\mathrm{7}} {\sum}}\frac{\mathrm{1}}{{n}}\:=\:\frac{\mathrm{1}}{\mathrm{7}}×\frac{\mathrm{363}}{\mathrm{140}}\:=\:\frac{\mathrm{363}}{\mathrm{980}} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 04/Oct/20

$$\mathrm{Great}\:\mathrm{sir}! \\ $$
