Menu Close

If-tan-and-tan-are-the-roots-of-equation-2x-2-5x-1-0-find-tan-2-2-tan-2-2-

Tinku Tara 0 Comments
Pin




Question Number 116503 by bemath last updated on 04/Oct/20
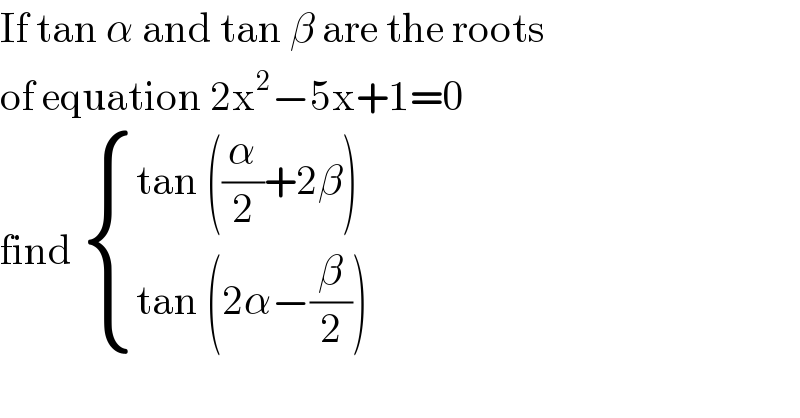
If tan α and tan β are the roots of equation 2x^2 −5x+1=0 find { ((tan ((α/2)+2β))),((tan (2α−(β/2)))) :}
$$\mathrm{If}\:\mathrm{tan}\:\alpha\:\mathrm{and}\:\mathrm{tan}\:\beta\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\: \\ $$$$\mathrm{of}\:\mathrm{equation}\:\mathrm{2x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{find}\:\begin{cases}{\mathrm{tan}\:\left(\frac{\alpha}{\mathrm{2}}+\mathrm{2}\beta\right)}\\{\mathrm{tan}\:\left(\mathrm{2}\alpha−\frac{\beta}{\mathrm{2}}\right)}\end{cases} \\ $$
Answered by bobhans last updated on 04/Oct/20
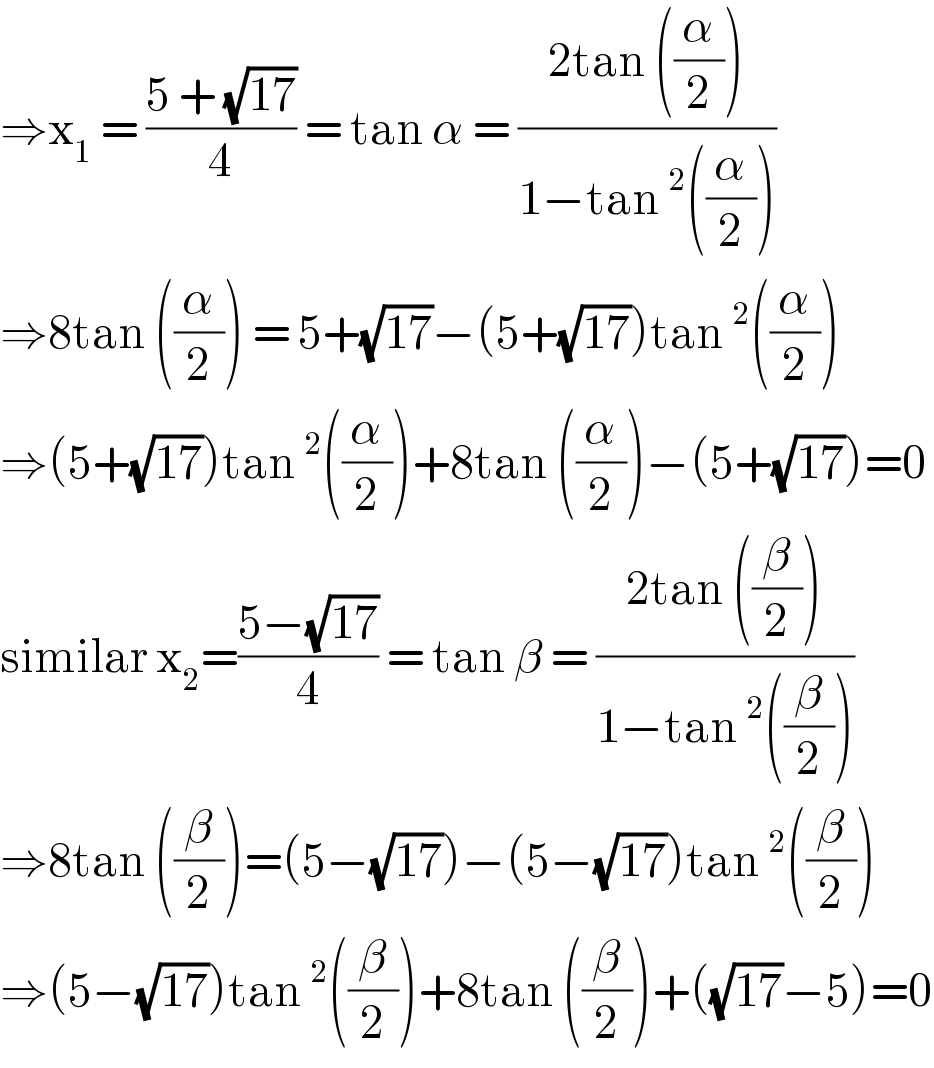
⇒x_1 = ((5 + (√(17)))/4) = tan α = ((2tan ((α/2)))/(1−tan^2 ((α/2)))) ⇒8tan ((α/2)) = 5+(√(17))−(5+(√(17)))tan^2 ((α/2)) ⇒(5+(√(17)))tan^2 ((α/2))+8tan ((α/2))−(5+(√(17)))=0 similar x_2 =((5−(√(17)))/4) = tan β = ((2tan ((β/2)))/(1−tan^2 ((β/2)))) ⇒8tan ((β/2))=(5−(√(17)))−(5−(√(17)))tan^2 ((β/2)) ⇒(5−(√(17)))tan^2 ((β/2))+8tan ((β/2))+((√(17))−5)=0
$$\Rightarrow\mathrm{x}_{\mathrm{1}} \:=\:\frac{\mathrm{5}\:+\:\sqrt{\mathrm{17}}}{\mathrm{4}}\:=\:\mathrm{tan}\:\alpha\:=\:\frac{\mathrm{2tan}\:\left(\frac{\alpha}{\mathrm{2}}\right)}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right)} \\ $$$$\Rightarrow\mathrm{8tan}\:\left(\frac{\alpha}{\mathrm{2}}\right)\:=\:\mathrm{5}+\sqrt{\mathrm{17}}−\left(\mathrm{5}+\sqrt{\mathrm{17}}\right)\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right) \\ $$$$\Rightarrow\left(\mathrm{5}+\sqrt{\mathrm{17}}\right)\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right)+\mathrm{8tan}\:\left(\frac{\alpha}{\mathrm{2}}\right)−\left(\mathrm{5}+\sqrt{\mathrm{17}}\right)=\mathrm{0} \\ $$$$\mathrm{similar}\:\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{5}−\sqrt{\mathrm{17}}}{\mathrm{4}}\:=\:\mathrm{tan}\:\beta\:=\:\frac{\mathrm{2tan}\:\left(\frac{\beta}{\mathrm{2}}\right)}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)} \\ $$$$\Rightarrow\mathrm{8tan}\:\left(\frac{\beta}{\mathrm{2}}\right)=\left(\mathrm{5}−\sqrt{\mathrm{17}}\right)−\left(\mathrm{5}−\sqrt{\mathrm{17}}\right)\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right) \\ $$$$\Rightarrow\left(\mathrm{5}−\sqrt{\mathrm{17}}\right)\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)+\mathrm{8tan}\:\left(\frac{\beta}{\mathrm{2}}\right)+\left(\sqrt{\mathrm{17}}−\mathrm{5}\right)=\mathrm{0} \\ $$
Answered by TANMAY PANACEA last updated on 04/Oct/20
tanα=((5+(√(17)))/4)≈2.28≈tan(1.157 radian) tanβ=((5−(√(17)))/4)≈0.22≈tan(0.22 radian) using graph.and calculator... it is not solution but approach tan((α/2)+2β)=tan{(((1.157)/2)+2×0.22)radian}≈1.03 tan(2α−(β/2))=tan{(2×1.157−0.11)radian}=−1.36
$${tan}\alpha=\frac{\mathrm{5}+\sqrt{\mathrm{17}}}{\mathrm{4}}\approx\mathrm{2}.\mathrm{28}\approx{tan}\left(\mathrm{1}.\mathrm{157}\:{radian}\right) \\ $$$${tan}\beta=\frac{\mathrm{5}−\sqrt{\mathrm{17}}}{\mathrm{4}}\approx\mathrm{0}.\mathrm{22}\approx{tan}\left(\mathrm{0}.\mathrm{22}\:{radian}\right) \\ $$$${using}\:{graph}.{and}\:{calculator}… \\ $$$${it}\:{is}\:{not}\:{solution}\:{but}\:{approach} \\ $$$${tan}\left(\frac{\alpha}{\mathrm{2}}+\mathrm{2}\beta\right)={tan}\left\{\left(\frac{\mathrm{1}.\mathrm{157}}{\mathrm{2}}+\mathrm{2}×\mathrm{0}.\mathrm{22}\right){radian}\right\}\approx\mathrm{1}.\mathrm{03} \\ $$$${tan}\left(\mathrm{2}\alpha−\frac{\beta}{\mathrm{2}}\right)={tan}\left\{\left(\mathrm{2}×\mathrm{1}.\mathrm{157}−\mathrm{0}.\mathrm{11}\right){radian}\right\}=−\mathrm{1}.\mathrm{36} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *