Question Number 50987 by naka3546 last updated on 23/Dec/18
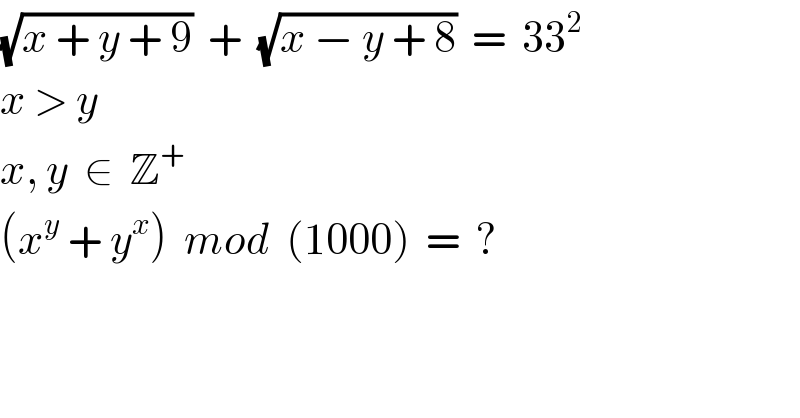
$$\sqrt{{x}\:+\:{y}\:+\:\mathrm{9}}\:\:+\:\:\sqrt{{x}\:−\:{y}\:+\:\mathrm{8}}\:\:=\:\:\mathrm{33}^{\mathrm{2}} \\ $$$${x}\:>\:{y} \\ $$$${x},\:{y}\:\:\in\:\:\mathbb{Z}^{+} \\ $$$$\left({x}^{{y}} \:+\:{y}^{{x}} \right)\:\:{mod}\:\:\left(\mathrm{1000}\right)\:\:=\:\:? \\ $$
Commented by Rasheed.Sindhi last updated on 23/Dec/18

$${No}\:{unique}\:{answer}. \\ $$$${For}\:{example}: \\ $$$${x}=\mathrm{320},{y}=\mathrm{247} \\ $$$$\:\:\:\:\:\left(\mathrm{320}^{\mathrm{247}} +\mathrm{247}^{\mathrm{320}} \right){mod}\:\mathrm{1000}=\mathrm{401} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{AND} \\ $$$${x}=\mathrm{336},{y}=\mathrm{280} \\ $$$$\:\:\:\:\:\left(\mathrm{336}^{\mathrm{280}} +\mathrm{280}^{\mathrm{336}} \right){mod}\:\mathrm{1000}=\mathrm{176} \\ $$
Commented by naka3546 last updated on 23/Dec/18
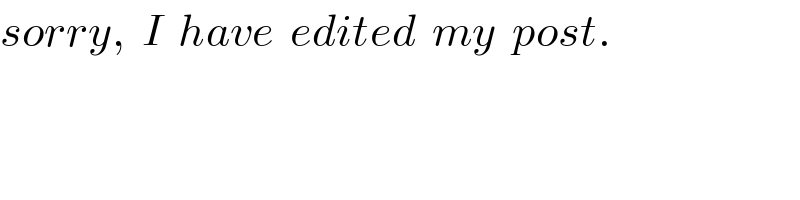
$${sorry},\:\:{I}\:\:{have}\:\:{edited}\:\:{my}\:\:{post}. \\ $$
