Question Number 116529 by mr W last updated on 04/Oct/20
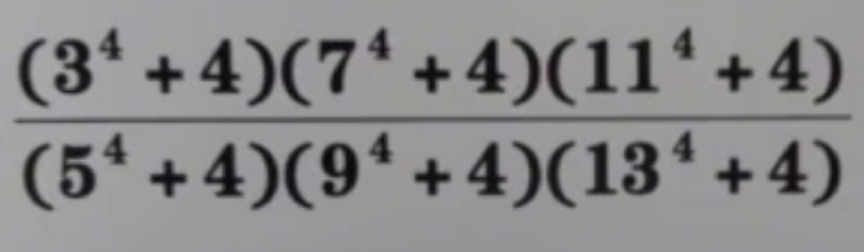
Commented by MJS_new last updated on 04/Oct/20

$$\frac{\mathrm{5}}{\mathrm{197}} \\ $$
Answered by maths mind last updated on 05/Oct/20
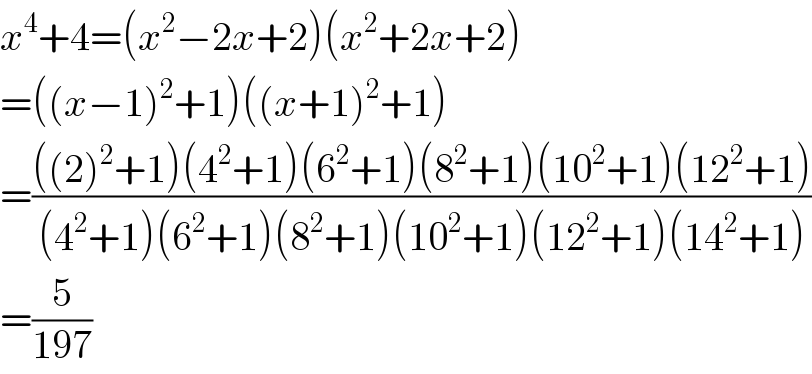
$${x}^{\mathrm{4}} +\mathrm{4}=\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right) \\ $$$$=\left(\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right)\left(\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$=\frac{\left(\left(\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{4}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{6}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{8}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{10}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{12}^{\mathrm{2}} +\mathrm{1}\right)}{\left(\mathrm{4}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{6}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{8}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{10}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{12}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{14}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{5}}{\mathrm{197}} \\ $$
Commented by mr W last updated on 05/Oct/20

$${great}! \\ $$
