Question Number 50996 by rahul 19 last updated on 23/Dec/18

$${Find}\:{the}\:{minimum}\:{value}\:{of} \\ $$$${f}\left({x}\right)=\:\mathrm{9tan}^{\mathrm{2}} \theta+\mathrm{4cot}^{\mathrm{2}} \theta\:? \\ $$
Commented by rahul 19 last updated on 23/Dec/18

$${f}\left({x}\right)=\:\left(\mathrm{3tan}\theta\right)^{\mathrm{2}} +\left(\mathrm{2cot}\theta\right)^{\mathrm{2}} +\mathrm{12}−\mathrm{12} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{3}{tan}\theta+\mathrm{2cot}\theta\right)^{\mathrm{2}} −\mathrm{12} \\ $$$$\Rightarrow\:{Minimum}\:{Value}\:=\:−\mathrm{12}. \\ $$
Commented by rahul 19 last updated on 23/Dec/18

$${Where}\:{am}\:{i}\:{wrong}? \\ $$$${Ans}\:{is}\:+\mathrm{12}. \\ $$
Commented by mr W last updated on 23/Dec/18
![f(x)=(3tanθ+2cotθ)^2 −12 is correct, but you can not say minimum of f(x) is −12, since the minimum of (3tanθ+2cotθ)^2 is not zero! in fact the minimum of (3tanθ+2cotθ)^2 is 24, therefore the minimum of f(x) is 24−12=12. so be careful when using the form f(x)=(....)^2 +c, its mininum is c only if the minimum of (....)^2 is zero! look at an example: f(x)=(x^2 +2x+3)^2 −1 its minimum is not −1, since minimum of (x^2 +2x+3)^2 is not zero, but 4, because (x^2 +2x+3)^2 =[(x+1)^2 +2]^2 ≥2^2 =4. i.e. the minimum of f(x) is 3. therefore when you are using f(x)=(....)^2 +c, you should arrange the formula in the way that (....)^2 can be zero, only then the minimum of f(x) is c. this is what you have had done in your example: f(x)= (3tanθ)^2 +(2cotθ)^2 −12+12 = (3tanθ−2cotθ)^2 +12 ⇒ Minimum Value = 12.](https://www.tinkutara.com/question/Q51020.png)
$${f}\left({x}\right)=\left(\mathrm{3}{tan}\theta+\mathrm{2cot}\theta\right)^{\mathrm{2}} −\mathrm{12}\:{is}\:{correct}, \\ $$$${but}\:{you}\:{can}\:{not}\:{say}\:{minimum}\:{of}\:{f}\left({x}\right) \\ $$$${is}\:−\mathrm{12},\:{since}\:{the}\:{minimum}\:{of} \\ $$$$\left(\mathrm{3}{tan}\theta+\mathrm{2cot}\theta\right)^{\mathrm{2}} \:{is}\:{not}\:{zero}!\:{in}\:{fact} \\ $$$${the}\:{minimum}\:{of}\:\left(\mathrm{3}{tan}\theta+\mathrm{2cot}\theta\right)^{\mathrm{2}} \:{is}\:\mathrm{24}, \\ $$$${therefore}\:{the}\:{minimum}\:{of}\:{f}\left({x}\right)\:{is} \\ $$$$\mathrm{24}−\mathrm{12}=\mathrm{12}.\:{so}\:{be}\:{careful}\:{when}\:{using} \\ $$$${the}\:{form}\:{f}\left({x}\right)=\left(….\right)^{\mathrm{2}} +{c},\:{its}\:{mininum} \\ $$$${is}\:{c}\:{only}\:{if}\:{the}\:{minimum}\:{of}\:\left(….\right)^{\mathrm{2}} \:{is} \\ $$$${zero}!\:{look}\:{at}\:{an}\:{example}: \\ $$$${f}\left({x}\right)=\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$${its}\:{minimum}\:{is}\:{not}\:−\mathrm{1},\:{since}\:{minimum}\:{of} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} \:{is}\:{not}\:{zero},\:{but}\:\mathrm{4},\:{because} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} =\left[\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}\right]^{\mathrm{2}} \geqslant\mathrm{2}^{\mathrm{2}} =\mathrm{4}.\:{i}.{e}. \\ $$$${the}\:{minimum}\:{of}\:{f}\left({x}\right)\:{is}\:\mathrm{3}. \\ $$$${therefore}\:{when}\:{you}\:{are}\:{using} \\ $$$${f}\left({x}\right)=\left(….\right)^{\mathrm{2}} +{c},\:{you}\:{should}\:{arrange}\:{the} \\ $$$${formula}\:{in}\:{the}\:{way}\:{that}\:\left(….\right)^{\mathrm{2}} \:{can}\:{be} \\ $$$${zero},\:{only}\:{then}\:{the}\:{minimum}\:{of}\:{f}\left({x}\right) \\ $$$${is}\:{c}. \\ $$$${this}\:{is}\:{what}\:{you}\:{have}\:{had}\:{done}\:{in}\:{your} \\ $$$${example}: \\ $$$${f}\left({x}\right)=\:\left(\mathrm{3tan}\theta\right)^{\mathrm{2}} +\left(\mathrm{2cot}\theta\right)^{\mathrm{2}} −\mathrm{12}+\mathrm{12} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{3}{tan}\theta−\mathrm{2cot}\theta\right)^{\mathrm{2}} +\mathrm{12} \\ $$$$\Rightarrow\:{Minimum}\:{Value}\:=\:\mathrm{12}. \\ $$
Commented by rahul 19 last updated on 23/Dec/18

$${Sir},\:{how}\:{min}.\:{value}\:{of}\: \\ $$$$\left(\mathrm{3tan}\theta+\mathrm{2cot}\theta\right)^{\mathrm{2}} =\:\mathrm{24}\:? \\ $$
Commented by mr W last updated on 23/Dec/18

$$\left(\mathrm{3}{x}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} \geqslant\left(\mathrm{2}\sqrt{\mathrm{3}{x}×\frac{\mathrm{2}}{{x}}}\right)^{\mathrm{2}} =\left(\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{2}} =\mathrm{24} \\ $$
Commented by rahul 19 last updated on 23/Dec/18

$$\left.{Thank}\:{you}\:{Sir}!:\right) \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18

$$\left(\mathrm{3}{x}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} =\left(\mathrm{3}{x}−\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} +\mathrm{4}×\mathrm{3}{x}×\frac{\mathrm{2}}{{x}} \\ $$$$\left(\mathrm{3}{x}−\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} \:{always}\:+{ve}\: \\ $$$${so}\:{for}\:{min}\:\left(\mathrm{3}{x}−\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${hence}\:{min}\:{value}\:=\mathrm{4}×\mathrm{3}{x}×\frac{\mathrm{2}}{{x}}=\mathrm{24} \\ $$
Commented by 951172235v last updated on 04/Feb/19
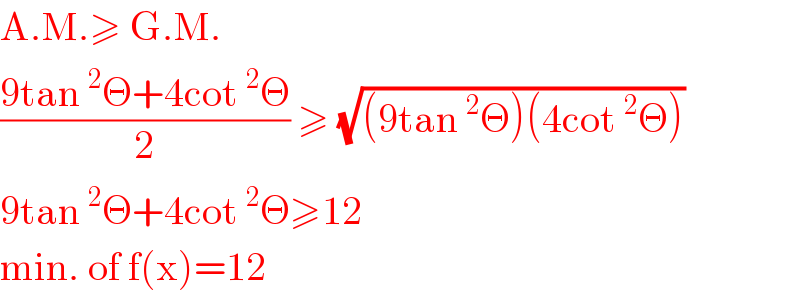
$$\mathrm{A}.\mathrm{M}.\geqslant\:\mathrm{G}.\mathrm{M}. \\ $$$$\frac{\mathrm{9tan}\:^{\mathrm{2}} \Theta+\mathrm{4cot}\:^{\mathrm{2}} \Theta}{\mathrm{2}}\:\geqslant\:\sqrt{\left(\mathrm{9tan}\:^{\mathrm{2}} \Theta\right)\left(\mathrm{4cot}\:^{\mathrm{2}} \Theta\right)} \\ $$$$\mathrm{9tan}\:^{\mathrm{2}} \Theta+\mathrm{4cot}\:^{\mathrm{2}} \Theta\geqslant\mathrm{12} \\ $$$$\mathrm{min}.\:\mathrm{of}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{12} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18

$$\left(\mathrm{3}{x}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{3}{x}−\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} +\mathrm{12} \\ $$$$\left(\mathrm{3}{x}−\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} ={alaways}\:+{ve} \\ $$$${so}\:{f}\left({x}\right)\:{is}\:{minimum}\:{when}\:\left(\mathrm{3}{x}−\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} =\mathrm{2}\:{at}\:{x}=\pm\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\: \\ $$$${f}\left({x}\right)\:{min}\:{value}\:\mathrm{12} \\ $$
Commented by rahul 19 last updated on 23/Dec/18

$${Thank}\:{you}\:{Sir}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18

$${most}\:{welcome}… \\ $$
