Question Number 182192 by mr W last updated on 05/Dec/22

Commented by mr W last updated on 05/Dec/22
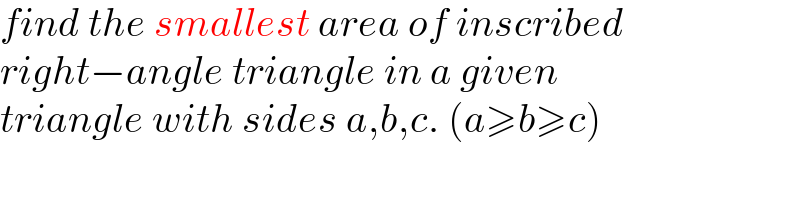
$${find}\:{the}\:{smallest}\:{area}\:{of}\:{inscribed} \\ $$$${right}−{angle}\:{triangle}\:{in}\:{a}\:{given} \\ $$$${triangle}\:{with}\:{sides}\:{a},{b},{c}.\:\left({a}\geqslant{b}\geqslant{c}\right) \\ $$
Answered by mr W last updated on 06/Dec/22

Commented by mr W last updated on 06/Dec/22
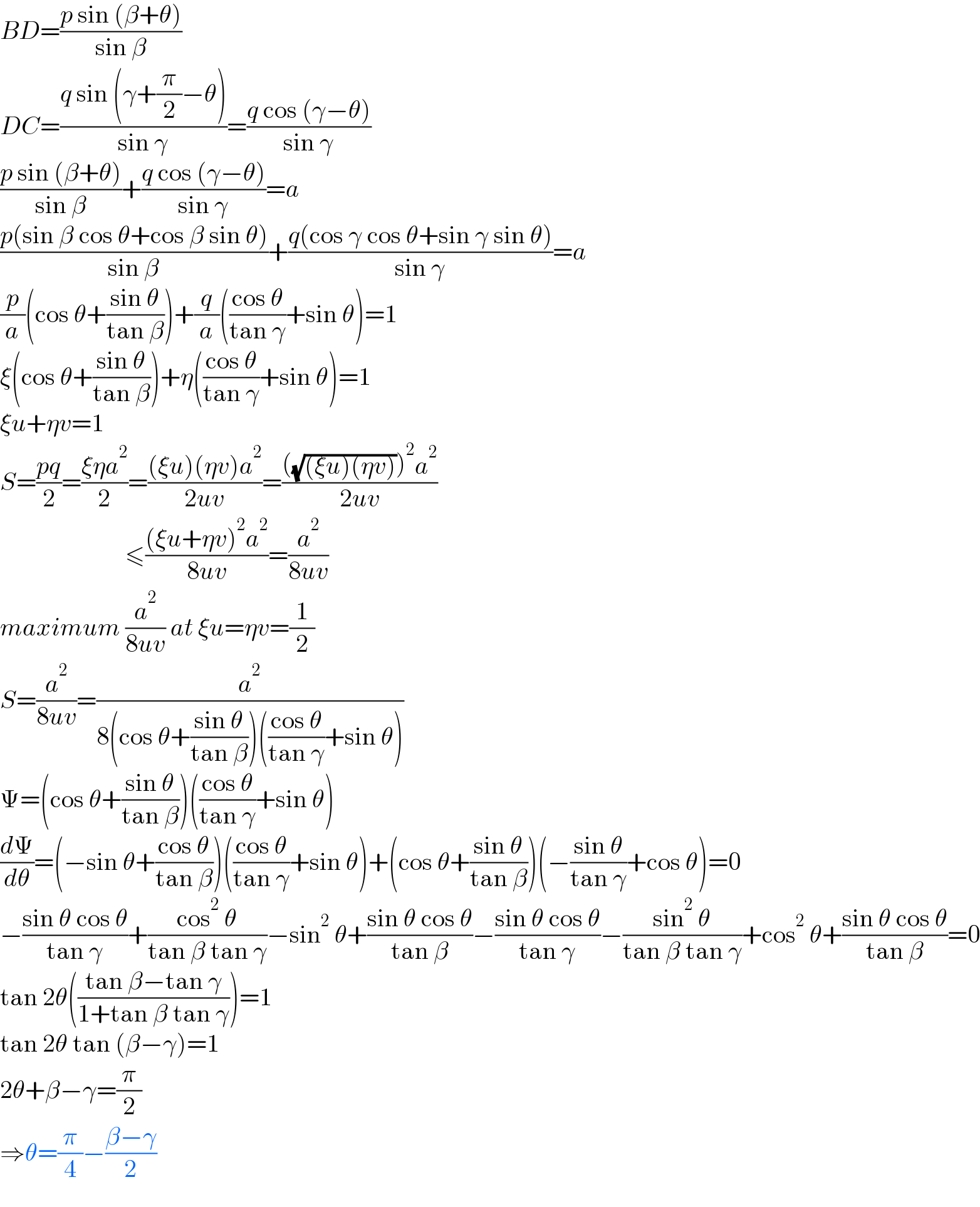
$${BD}=\frac{{p}\:\mathrm{sin}\:\left(\beta+\theta\right)}{\mathrm{sin}\:\beta} \\ $$$${DC}=\frac{{q}\:\mathrm{sin}\:\left(\gamma+\frac{\pi}{\mathrm{2}}−\theta\right)}{\mathrm{sin}\:\gamma}=\frac{{q}\:\mathrm{cos}\:\left(\gamma−\theta\right)}{\mathrm{sin}\:\gamma} \\ $$$$\frac{{p}\:\mathrm{sin}\:\left(\beta+\theta\right)}{\mathrm{sin}\:\beta}+\frac{{q}\:\mathrm{cos}\:\left(\gamma−\theta\right)}{\mathrm{sin}\:\gamma}={a} \\ $$$$\frac{{p}\left(\mathrm{sin}\:\beta\:\mathrm{cos}\:\theta+\mathrm{cos}\:\beta\:\mathrm{sin}\:\theta\right)}{\mathrm{sin}\:\beta}+\frac{{q}\left(\mathrm{cos}\:\gamma\:\mathrm{cos}\:\theta+\mathrm{sin}\:\gamma\:\mathrm{sin}\:\theta\right)}{\mathrm{sin}\:\gamma}={a} \\ $$$$\frac{{p}}{{a}}\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\beta}\right)+\frac{{q}}{{a}}\left(\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\gamma}+\mathrm{sin}\:\theta\right)=\mathrm{1} \\ $$$$\xi\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\beta}\right)+\eta\left(\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\gamma}+\mathrm{sin}\:\theta\right)=\mathrm{1} \\ $$$$\xi{u}+\eta{v}=\mathrm{1} \\ $$$${S}=\frac{{pq}}{\mathrm{2}}=\frac{\xi\eta{a}^{\mathrm{2}} }{\mathrm{2}}=\frac{\left(\xi{u}\right)\left(\eta{v}\right){a}^{\mathrm{2}} }{\mathrm{2}{uv}}=\frac{\left(\sqrt{\left(\xi{u}\right)\left(\eta{v}\right)}\right)^{\mathrm{2}} {a}^{\mathrm{2}} }{\mathrm{2}{uv}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\leqslant\frac{\left(\xi{u}+\eta{v}\right)^{\mathrm{2}} {a}^{\mathrm{2}} }{\mathrm{8}{uv}}=\frac{{a}^{\mathrm{2}} }{\mathrm{8}{uv}} \\ $$$${maximum}\:\frac{{a}^{\mathrm{2}} }{\mathrm{8}{uv}}\:{at}\:\xi{u}=\eta{v}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${S}=\frac{{a}^{\mathrm{2}} }{\mathrm{8}{uv}}=\frac{{a}^{\mathrm{2}} }{\mathrm{8}\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\beta}\right)\left(\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\gamma}+\mathrm{sin}\:\theta\right)} \\ $$$$\Psi=\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\beta}\right)\left(\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\gamma}+\mathrm{sin}\:\theta\right) \\ $$$$\frac{{d}\Psi}{{d}\theta}=\left(−\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\beta}\right)\left(\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\gamma}+\mathrm{sin}\:\theta\right)+\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\beta}\right)\left(−\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\gamma}+\mathrm{cos}\:\theta\right)=\mathrm{0} \\ $$$$−\frac{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\mathrm{tan}\:\gamma}+\frac{\mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{tan}\:\beta\:\mathrm{tan}\:\gamma}−\mathrm{sin}^{\mathrm{2}} \:\theta+\frac{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\mathrm{tan}\:\beta}−\frac{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\mathrm{tan}\:\gamma}−\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{tan}\:\beta\:\mathrm{tan}\:\gamma}+\mathrm{cos}^{\mathrm{2}} \:\theta+\frac{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\mathrm{tan}\:\beta}=\mathrm{0} \\ $$$$\mathrm{tan}\:\mathrm{2}\theta\left(\frac{\mathrm{tan}\:\beta−\mathrm{tan}\:\gamma}{\mathrm{1}+\mathrm{tan}\:\beta\:\mathrm{tan}\:\gamma}\right)=\mathrm{1} \\ $$$$\mathrm{tan}\:\mathrm{2}\theta\:\mathrm{tan}\:\left(\beta−\gamma\right)=\mathrm{1} \\ $$$$\mathrm{2}\theta+\beta−\gamma=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\frac{\pi}{\mathrm{4}}−\frac{\beta−\gamma}{\mathrm{2}} \\ $$
Commented by mr W last updated on 06/Dec/22

Commented by mr W last updated on 07/Dec/22
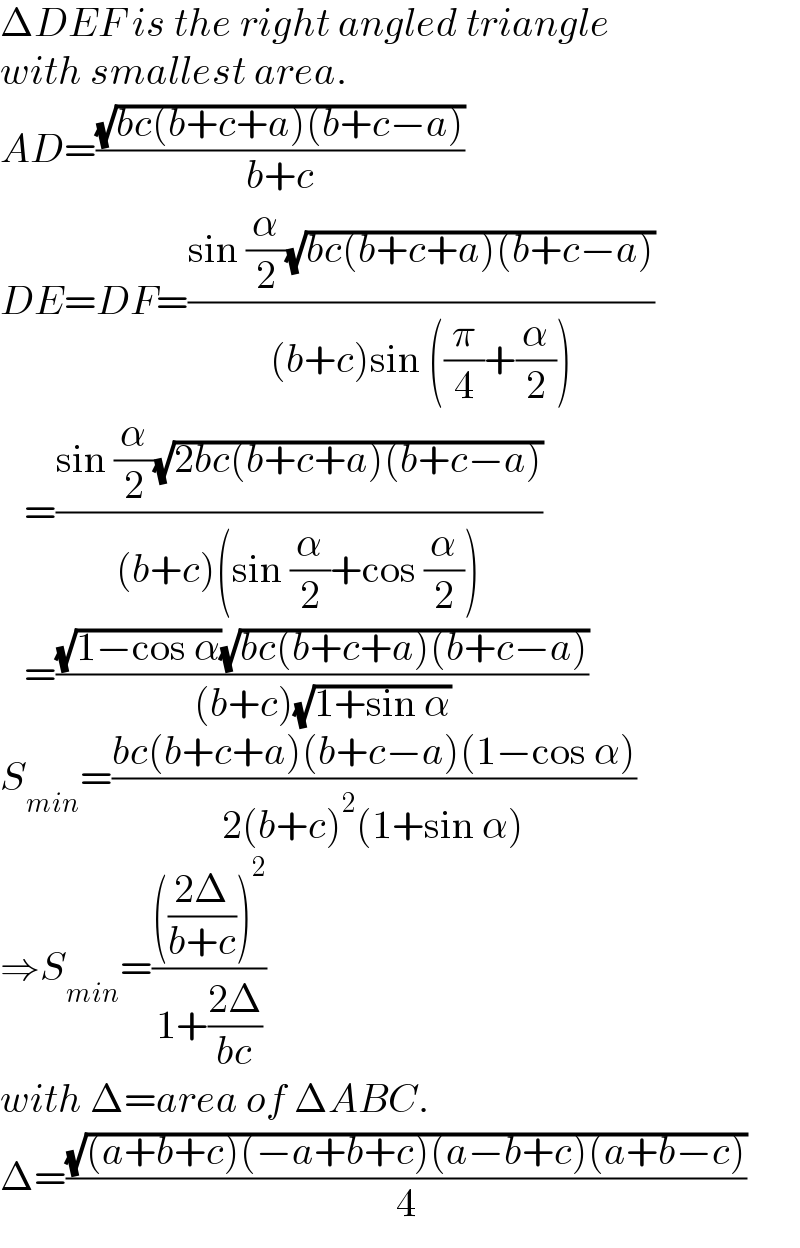
$$\Delta{DEF}\:{is}\:{the}\:{right}\:{angled}\:{triangle} \\ $$$${with}\:{smallest}\:{area}. \\ $$$${AD}=\frac{\sqrt{{bc}\left({b}+{c}+{a}\right)\left({b}+{c}−{a}\right)}}{{b}+{c}} \\ $$$${DE}={DF}=\frac{\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\sqrt{{bc}\left({b}+{c}+{a}\right)\left({b}+{c}−{a}\right)}}{\left({b}+{c}\right)\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+\frac{\alpha}{\mathrm{2}}\right)} \\ $$$$\:\:\:=\frac{\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\sqrt{\mathrm{2}{bc}\left({b}+{c}+{a}\right)\left({b}+{c}−{a}\right)}}{\left({b}+{c}\right)\left(\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}+\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)} \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{1}−\mathrm{cos}\:\alpha}\sqrt{{bc}\left({b}+{c}+{a}\right)\left({b}+{c}−{a}\right)}}{\left({b}+{c}\right)\sqrt{\mathrm{1}+\mathrm{sin}\:\alpha}} \\ $$$${S}_{{min}} =\frac{{bc}\left({b}+{c}+{a}\right)\left({b}+{c}−{a}\right)\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)}{\mathrm{2}\left({b}+{c}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{sin}\:\alpha\right)} \\ $$$$\Rightarrow{S}_{{min}} =\frac{\left(\frac{\mathrm{2}\Delta}{{b}+{c}}\right)^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{2}\Delta}{{bc}}} \\ $$$${with}\:\Delta={area}\:{of}\:\Delta{ABC}. \\ $$$$\Delta=\frac{\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}{\mathrm{4}} \\ $$
