Question Number 116683 by mathocean1 last updated on 05/Oct/20

$$\mathrm{Given}\:\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}=\mathrm{16}\:\:\:\mathrm{we}\:\mathrm{know}\:\mathrm{that} \\ $$$$\mathrm{16}=\mathrm{4}^{\mathrm{2}} \:\:\mathrm{and}\:\mathrm{4}\:\mathrm{is}\:\mathrm{the}\:\mathrm{half}\:\mathrm{of}\:\mathrm{8}\:\mathrm{which}\:\mathrm{is}\:\mathrm{the}\: \\ $$$$\mathrm{successor}\:\mathrm{of}\:\mathrm{7}. \\ $$$$ \\ $$$$\mathrm{conjecture}\:\mathrm{the}\:\mathrm{result}\:\mathrm{of}\:\mathrm{this}\:\mathrm{sum}: \\ $$$$\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}+…+\mathrm{25} \\ $$
Answered by Dwaipayan Shikari last updated on 05/Oct/20
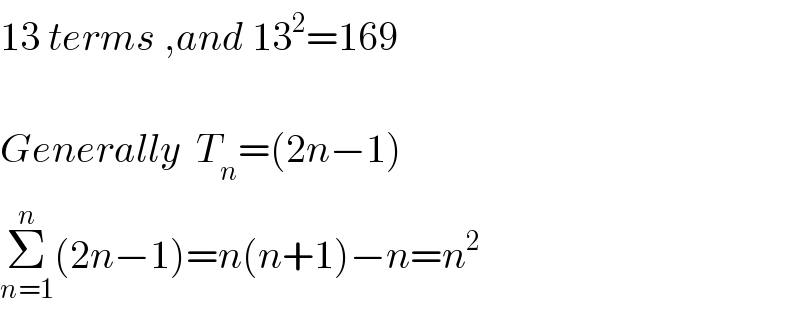
$$\mathrm{13}\:{terms}\:,{and}\:\mathrm{13}^{\mathrm{2}} =\mathrm{169} \\ $$$$ \\ $$$${Generally}\:\:{T}_{{n}} =\left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{2}{n}−\mathrm{1}\right)={n}\left({n}+\mathrm{1}\right)−{n}={n}^{\mathrm{2}} \\ $$
Commented by mathocean1 last updated on 05/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$$$ \\ $$
Answered by $@y@m last updated on 06/Oct/20
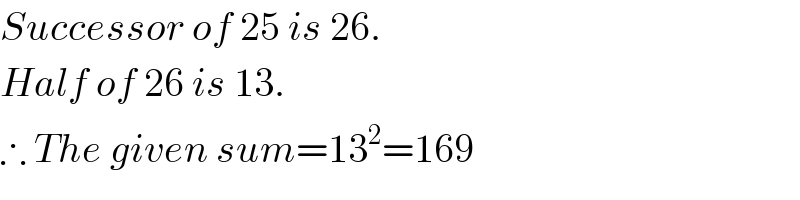
$${Successor}\:{of}\:\mathrm{25}\:{is}\:\mathrm{26}. \\ $$$${Half}\:{of}\:\mathrm{26}\:{is}\:\mathrm{13}. \\ $$$$\therefore\:{The}\:{given}\:{sum}=\mathrm{13}^{\mathrm{2}} =\mathrm{169} \\ $$
