Question Number 51150 by peter frank last updated on 24/Dec/18
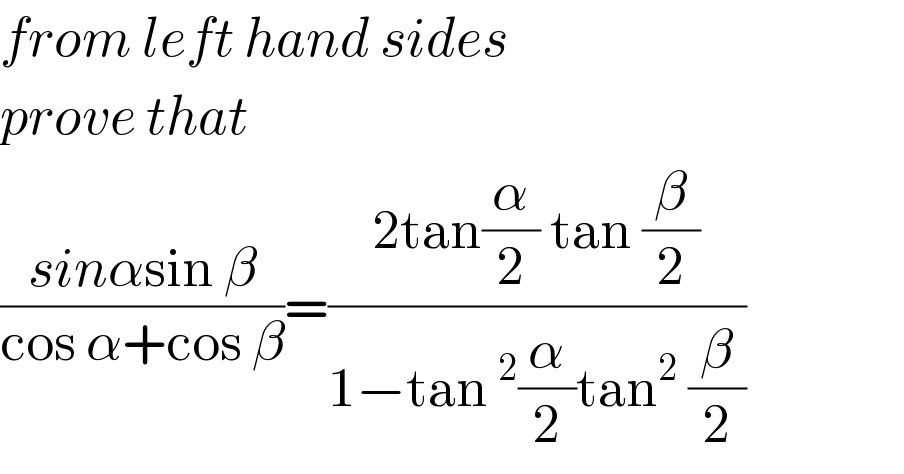
$${from}\:{left}\:{hand}\:{sides} \\ $$$${prove}\:{that} \\ $$$$\frac{{sin}\alpha\mathrm{sin}\:\beta}{\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta}=\frac{\mathrm{2tan}\frac{\alpha}{\mathrm{2}}\:\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}\mathrm{tan}^{\mathrm{2}} \:\frac{\beta}{\mathrm{2}}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Dec/18
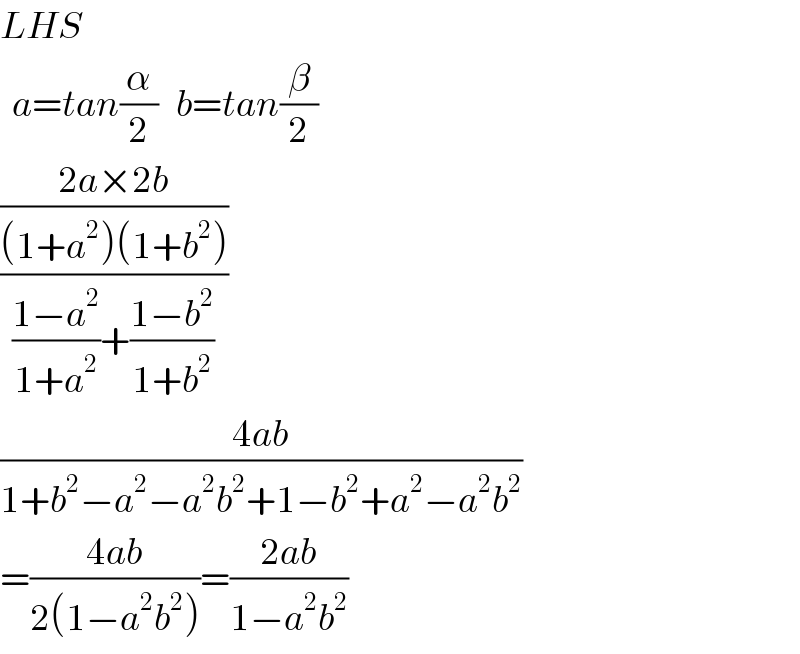
$${LHS} \\ $$$$\:\:{a}={tan}\frac{\alpha}{\mathrm{2}}\:\:\:{b}={tan}\frac{\beta}{\mathrm{2}} \\ $$$$\frac{\frac{\mathrm{2}{a}×\mathrm{2}{b}}{\left(\mathrm{1}+{a}^{\mathrm{2}} \right)\left(\mathrm{1}+{b}^{\mathrm{2}} \right)}}{\frac{\mathrm{1}−{a}^{\mathrm{2}} }{\mathrm{1}+{a}^{\mathrm{2}} }+\frac{\mathrm{1}−{b}^{\mathrm{2}} }{\mathrm{1}+{b}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{4}{ab}}{\mathrm{1}+{b}^{\mathrm{2}} −{a}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{1}−{b}^{\mathrm{2}} +{a}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{4}{ab}}{\mathrm{2}\left(\mathrm{1}−{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)}=\frac{\mathrm{2}{ab}}{\mathrm{1}−{a}^{\mathrm{2}} {b}^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 24/Dec/18

$${very}\:{nice}\:{Sir}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 24/Dec/18

$${thank}\:{you}\:{sir}… \\ $$
Commented by peter frank last updated on 24/Dec/18

$${thank}\:{you} \\ $$
Answered by peter frank last updated on 25/Dec/18

$$\frac{{sin}\alpha\mathrm{sin}\:\beta}{\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta}=\frac{\mathrm{4sin}\:\frac{\alpha}{\mathrm{2}}\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}.\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\mathrm{cos}\:\frac{\beta}{\mathrm{2}}}{{cos}\alpha+\mathrm{sin}\:\beta} \\ $$$$\mathrm{cos}\:\alpha=\mathrm{cos}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}−\mathrm{sin}\:^{\mathrm{2}} \frac{\alpha}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\beta=\mathrm{cos}^{\mathrm{2}} \:\frac{\beta}{\mathrm{2}}−\mathrm{sin}\:^{\mathrm{2}} \frac{\beta}{\mathrm{2}} \\ $$$$\frac{\mathrm{4sin}\:\frac{\alpha}{\mathrm{2}}\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}.\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\mathrm{cos}\:\frac{\beta}{\mathrm{2}}}{\left(\mathrm{cos}\:^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}−\mathrm{sin}^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}\right)+\left(\mathrm{cos}\:^{\mathrm{2}} \frac{\beta}{\mathrm{2}}−\mathrm{sin}\:^{\mathrm{2}} \frac{\beta}{\mathrm{2}}\right)} \\ $$$${divide}\:{by}\:\mathrm{cos}\:^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}\mathrm{cos}\:^{\mathrm{2}} \frac{\beta}{\mathrm{2}}\:{both}\:\:{numerator}\:{and}\:{denominator} \\ $$$$\frac{\mathrm{4tan}\:\frac{\alpha}{\mathrm{2}}\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}{\mathrm{sec}\:^{\mathrm{2}} \frac{\beta}{\mathrm{2}}\left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\right)+\mathrm{sec}\:^{\mathrm{2}} \frac{\beta}{\mathrm{2}}\left(\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \frac{\beta}{\mathrm{2}}\right)} \\ $$$$ \\ $$$$\frac{\mathrm{4tan}\:\frac{\alpha}{\mathrm{2}}\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}{\mathrm{2}−\mathrm{2tan}\:^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}\mathrm{tan}\:^{\mathrm{2}} \frac{\beta}{\mathrm{2}}} \\ $$$$\frac{\mathrm{2tan}\:\frac{\alpha}{\mathrm{2}}\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}\mathrm{tan}\:^{\mathrm{2}} \frac{\beta}{\mathrm{2}}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
