Menu Close

Prove-that-a-If-z-1-z-2-z-1-z-2-the-difference-of-the-arguements-of-z-1-and-z-2-is-pi-2-b-If-arg-z-1-z-2-z-1-z-2-pi-2-then-z-1-z-2-

Tinku Tara 0 Comments
Pin




Question Number 51167 by Tawa1 last updated on 24/Dec/18
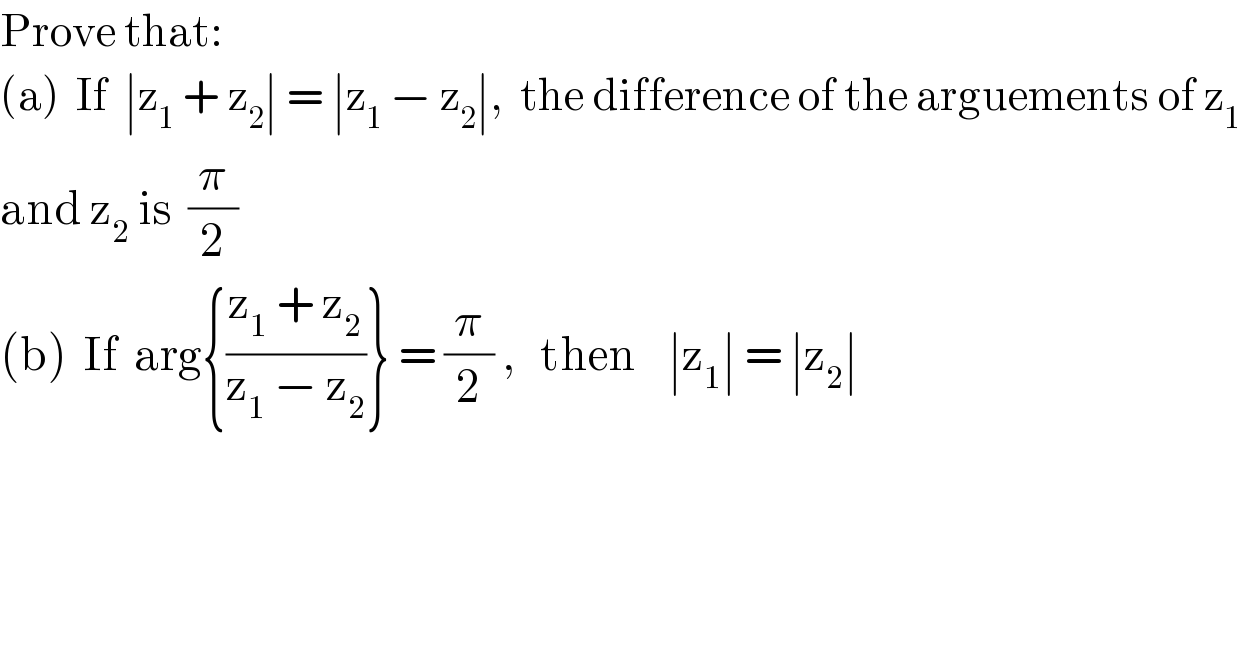
Prove that: (a) If ∣z_1 + z_2 ∣ = ∣z_1 − z_2 ∣, the difference of the arguements of z_1 and z_2 is (π/2) (b) If arg{((z_1 + z_2 )/(z_1 − z_2 ))} = (π/2) , then ∣z_1 ∣ = ∣z_2 ∣
$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\left(\mathrm{a}\right)\:\:\mathrm{If}\:\:\mid\mathrm{z}_{\mathrm{1}} \:+\:\mathrm{z}_{\mathrm{2}} \mid\:=\:\mid\mathrm{z}_{\mathrm{1}} \:−\:\mathrm{z}_{\mathrm{2}} \mid,\:\:\mathrm{the}\:\mathrm{difference}\:\mathrm{of}\:\mathrm{the}\:\mathrm{arguements}\:\mathrm{of}\:\mathrm{z}_{\mathrm{1}} \\ $$$$\mathrm{and}\:\mathrm{z}_{\mathrm{2}} \:\mathrm{is}\:\:\frac{\pi}{\mathrm{2}} \\ $$$$\left(\mathrm{b}\right)\:\:\mathrm{If}\:\:\mathrm{arg}\left\{\frac{\mathrm{z}_{\mathrm{1}} \:+\:\mathrm{z}_{\mathrm{2}} }{\mathrm{z}_{\mathrm{1}} \:−\:\mathrm{z}_{\mathrm{2}} }\right\}\:=\:\frac{\pi}{\mathrm{2}}\:,\:\:\:\mathrm{then}\:\:\:\:\mid\mathrm{z}_{\mathrm{1}} \mid\:=\:\mid\mathrm{z}_{\mathrm{2}} \mid \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Dec/18
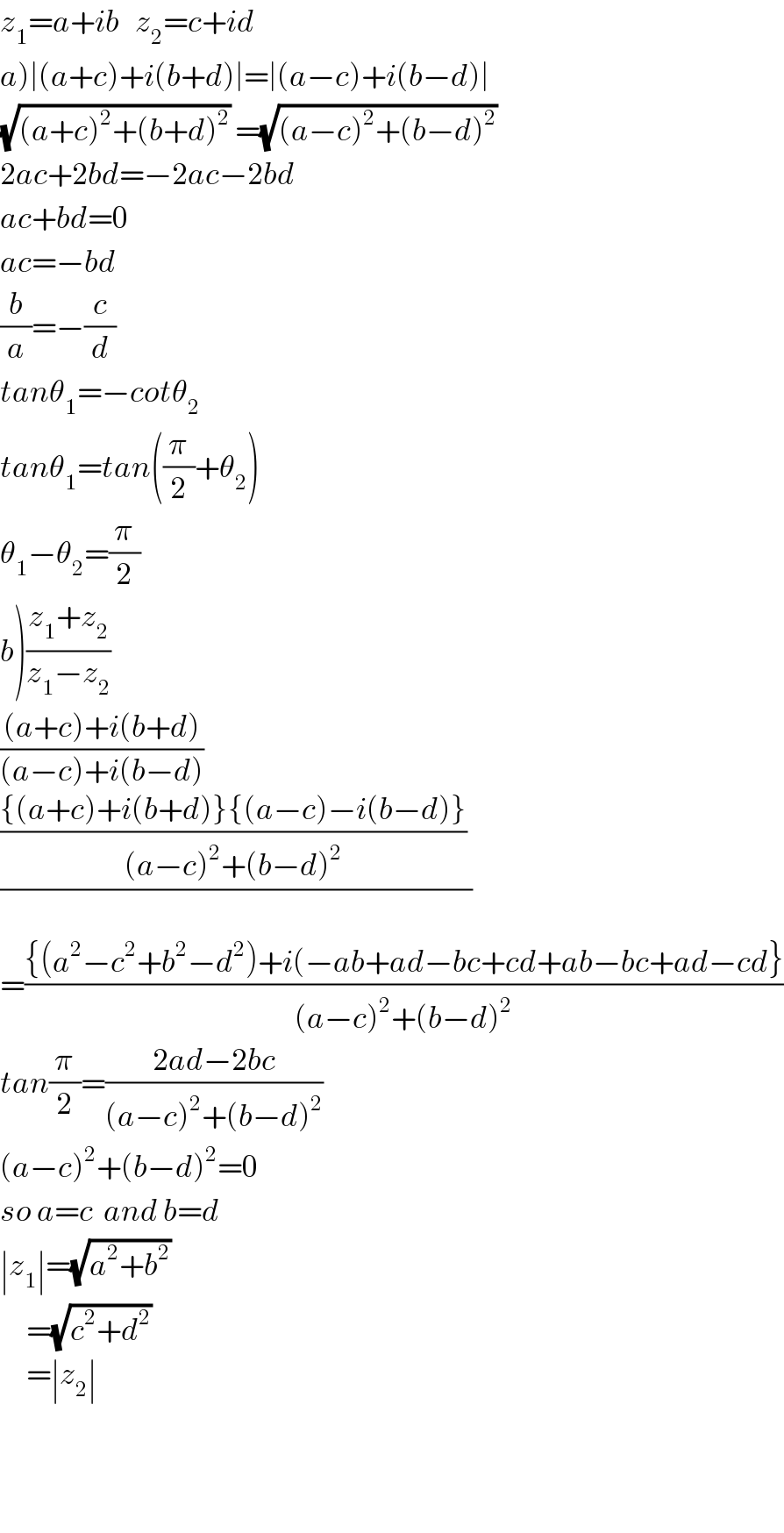
z_1 =a+ib z_2 =c+id a)∣(a+c)+i(b+d)∣=∣(a−c)+i(b−d)∣ (√((a+c)^2 +(b+d)^2 )) =(√((a−c)^2 +(b−d)^2 )) 2ac+2bd=−2ac−2bd ac+bd=0 ac=−bd (b/a)=−(c/d) tanθ_1 =−cotθ_2 tanθ_1 =tan((π/2)+θ_2 ) θ_1 −θ_2 =(π/2) b)((z_1 +z_2 )/(z_1 −z_2 )) (((a+c)+i(b+d))/((a−c)+i(b−d))) (((({(a+c)+i(b+d)}{(a−c)−i(b−d)})/((a−c)^2 +(b−d)^2 )) )/) =(({(a^2 −c^2 +b^2 −d^2 )+i(−ab+ad−bc+cd+ab−bc+ad−cd})/((a−c)^2 +(b−d)^2 )) tan(π/2)=((2ad−2bc)/((a−c)^2 +(b−d)^2 )) (a−c)^2 +(b−d)^2 =0 so a=c and b=d ∣z_1 ∣=(√(a^2 +b^2 )) =(√(c^2 +d^2 )) =∣z_2 ∣
$${z}_{\mathrm{1}} ={a}+{ib}\:\:\:{z}_{\mathrm{2}} ={c}+{id} \\ $$$$\left.{a}\right)\mid\left({a}+{c}\right)+{i}\left({b}+{d}\right)\mid=\mid\left({a}−{c}\right)+{i}\left({b}−{d}\right)\mid \\ $$$$\sqrt{\left({a}+{c}\right)^{\mathrm{2}} +\left({b}+{d}\right)^{\mathrm{2}} }\:=\sqrt{\left({a}−{c}\right)^{\mathrm{2}} +\left({b}−{d}\right)^{\mathrm{2}} }\: \\ $$$$\mathrm{2}{ac}+\mathrm{2}{bd}=−\mathrm{2}{ac}−\mathrm{2}{bd} \\ $$$${ac}+{bd}=\mathrm{0} \\ $$$${ac}=−{bd} \\ $$$$\frac{{b}}{{a}}=−\frac{{c}}{{d}} \\ $$$${tan}\theta_{\mathrm{1}} =−{cot}\theta_{\mathrm{2}} \\ $$$${tan}\theta_{\mathrm{1}} ={tan}\left(\frac{\pi}{\mathrm{2}}+\theta_{\mathrm{2}} \right) \\ $$$$\theta_{\mathrm{1}} −\theta_{\mathrm{2}} =\frac{\pi}{\mathrm{2}} \\ $$$$\left.{b}\right)\frac{{z}_{\mathrm{1}} +{z}_{\mathrm{2}} }{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} } \\ $$$$\frac{\left({a}+{c}\right)+{i}\left({b}+{d}\right)}{\left({a}−{c}\right)+{i}\left({b}−{d}\right)} \\ $$$$\frac{\frac{\left\{\left({a}+{c}\right)+{i}\left({b}+{d}\right)\right\}\left\{\left({a}−{c}\right)−{i}\left({b}−{d}\right)\right\}}{\left({a}−{c}\right)^{\mathrm{2}} +\left({b}−{d}\right)^{\mathrm{2}} }\:}{} \\ $$$$=\frac{\left\{\left({a}^{\mathrm{2}} −{c}^{\mathrm{2}} +{b}^{\mathrm{2}} −{d}^{\mathrm{2}} \right)+{i}\left(−{ab}+{ad}−{bc}+{cd}+{ab}−{bc}+{ad}−{cd}\right\}\right.}{\left({a}−{c}\right)^{\mathrm{2}} +\left({b}−{d}\right)^{\mathrm{2}} } \\ $$$${tan}\frac{\pi}{\mathrm{2}}=\frac{\mathrm{2}{ad}−\mathrm{2}{bc}}{\left({a}−{c}\right)^{\mathrm{2}} +\left({b}−{d}\right)^{\mathrm{2}} } \\ $$$$\left({a}−{c}\right)^{\mathrm{2}} +\left({b}−{d}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${so}\:{a}={c}\:\:{and}\:{b}={d} \\ $$$$\mid{z}_{\mathrm{1}} \mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\: \\ $$$$\:\:\:\:\:=\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }\: \\ $$$$\:\:\:\:\:=\mid{z}_{\mathrm{2}} \mid \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa1 last updated on 24/Dec/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 24/Dec/18
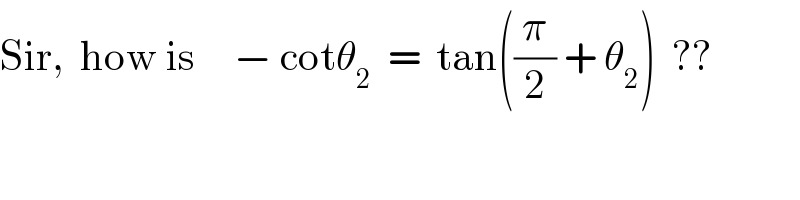
Sir, how is − cotθ_2 = tan((π/2) + θ_2 ) ??
$$\mathrm{Sir},\:\:\mathrm{how}\:\mathrm{is}\:\:\:\:\:−\:\mathrm{cot}\theta_{\mathrm{2}} \:\:=\:\:\mathrm{tan}\left(\frac{\pi}{\mathrm{2}}\:+\:\theta_{\mathrm{2}} \right)\:\:?? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 24/Dec/18
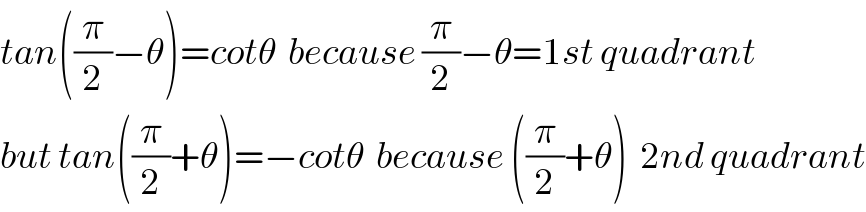
tan((π/2)−θ)=cotθ because (π/2)−θ=1st quadrant but tan((π/2)+θ)=−cotθ because ((π/2)+θ) 2nd quadrant
$${tan}\left(\frac{\pi}{\mathrm{2}}−\theta\right)={cot}\theta\:\:{because}\:\frac{\pi}{\mathrm{2}}−\theta=\mathrm{1}{st}\:{quadrant} \\ $$$${but}\:{tan}\left(\frac{\pi}{\mathrm{2}}+\theta\right)=−{cot}\theta\:\:{because}\:\left(\frac{\pi}{\mathrm{2}}+\theta\right)\:\:\mathrm{2}{nd}\:{quadrant} \\ $$
Commented by Tawa1 last updated on 24/Dec/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by peter frank last updated on 24/Dec/18
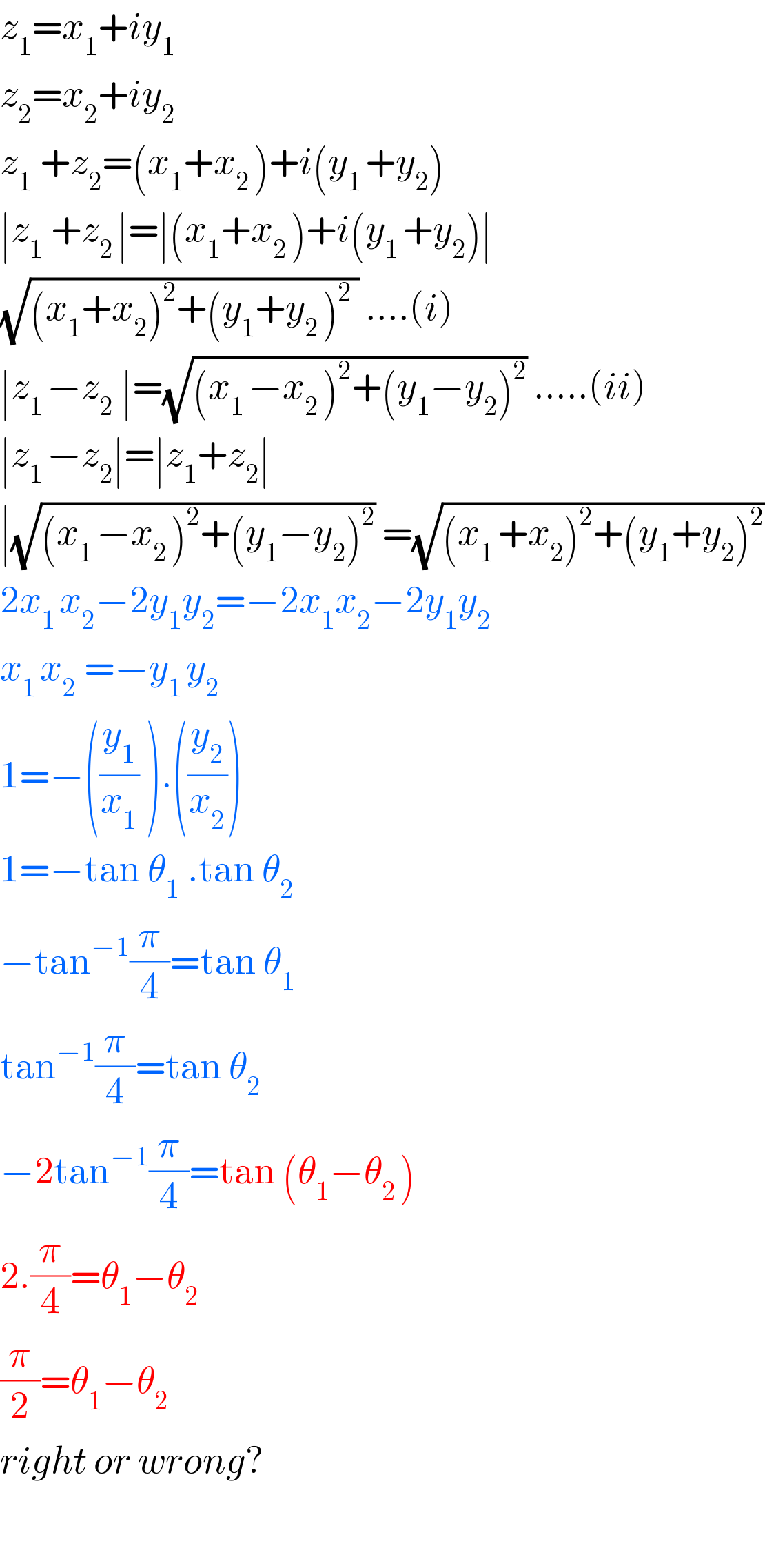
z_1 =x_1 +iy_1 z_2 =x_2 +iy_2 z_(1 ) +z_2 =(x_1 +x_(2 ) )+i(y_(1 ) +y_2 ) ∣z_(1 ) +z_(2 ) ∣=∣(x_1 +x_(2 ) )+i(y_(1 ) +y_2 )∣ (√((x_1 +x_2 )^2 +(y_1 +y_(2 ) )^2 )) ....(i) ∣z_(1 ) −z_(2 ) ∣=(√((x_(1 ) −x_(2 ) )^2 +(y_1 −y_2 )^2 )) .....(ii) ∣z_(1 ) −z_2 ∣=∣z_1 +z_2 ∣ ∣(√((x_(1 ) −x_(2 ) )^2 +(y_1 −y_2 )^2 )) =(√((x_(1 ) +x_2 )^2 +(y_1 +y_2 )^2 )) 2x_(1 ) x_2 −2y_1 y_2 =−2x_1 x_2 −2y_1 y_2 x_(1 ) x_(2 ) =−y_(1 ) y_2 1=−((y_1 /x_1 ) ).((y_2 /x_2 )) 1=−tan θ_(1 ) .tan θ_2 −tan^(−1) (π/4)=tan θ_1 tan^(−1) (π/4)=tan θ_(2 ) −2tan^(−1) (π/4)=tan (θ_1 −θ_(2 ) ) 2.(π/4)=θ_1 −θ_2 (π/2)=θ_1 −θ_2 right or wrong?
$${z}_{\mathrm{1}} ={x}_{\mathrm{1}} +{iy}_{\mathrm{1}} \\ $$$${z}_{\mathrm{2}} ={x}_{\mathrm{2}} +{iy}_{\mathrm{2}} \\ $$$${z}_{\mathrm{1}\:\:} +{z}_{\mathrm{2}} =\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}\:} \right)+{i}\left({y}_{\mathrm{1}\:} +{y}_{\mathrm{2}} \right) \\ $$$$\mid{z}_{\mathrm{1}\:\:} +{z}_{\mathrm{2}\:} \mid=\mid\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}\:} \right)+{i}\left({y}_{\mathrm{1}\:} +{y}_{\mathrm{2}} \right)\mid \\ $$$$\sqrt{\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)^{\mathrm{2}} +\left({y}_{\mathrm{1}} +{y}_{\mathrm{2}\:} \right)^{\mathrm{2}} \:}\:….\left({i}\right) \\ $$$$\mid{z}_{\mathrm{1}\:} −{z}_{\mathrm{2}\:\:} \mid=\sqrt{\left({x}_{\mathrm{1}\:} −{x}_{\mathrm{2}\:} \right)^{\mathrm{2}} +\left({y}_{\mathrm{1}} −{y}_{\mathrm{2}} \right)^{\mathrm{2}} }\:…..\left({ii}\right) \\ $$$$\mid{z}_{\mathrm{1}\:} −{z}_{\mathrm{2}} \mid=\mid{z}_{\mathrm{1}} +{z}_{\mathrm{2}} \mid \\ $$$$\mid\sqrt{\left({x}_{\mathrm{1}\:} −{x}_{\mathrm{2}\:} \right)^{\mathrm{2}} +\left({y}_{\mathrm{1}} −{y}_{\mathrm{2}} \right)^{\mathrm{2}} }\:=\sqrt{\left({x}_{\mathrm{1}\:} +{x}_{\mathrm{2}} \right)^{\mathrm{2}} +\left({y}_{\mathrm{1}} +{y}_{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{2}{x}_{\mathrm{1}\:} {x}_{\mathrm{2}} −\mathrm{2}{y}_{\mathrm{1}} {y}_{\mathrm{2}} =−\mathrm{2}{x}_{\mathrm{1}} {x}_{\mathrm{2}} −\mathrm{2}{y}_{\mathrm{1}} {y}_{\mathrm{2}} \\ $$$${x}_{\mathrm{1}\:} {x}_{\mathrm{2}\:\:} =−{y}_{\mathrm{1}\:} {y}_{\mathrm{2}} \\ $$$$\mathrm{1}=−\left(\frac{{y}_{\mathrm{1}} }{{x}_{\mathrm{1}} }\:\right).\left(\frac{{y}_{\mathrm{2}} }{{x}_{\mathrm{2}} }\right) \\ $$$$\mathrm{1}=−\mathrm{tan}\:\theta_{\mathrm{1}\:\:} .\mathrm{tan}\:\theta_{\mathrm{2}} \\ $$$$−\mathrm{tan}^{−\mathrm{1}} \frac{\pi}{\mathrm{4}}=\mathrm{tan}\:\theta_{\mathrm{1}} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \frac{\pi}{\mathrm{4}}=\mathrm{tan}\:\theta_{\mathrm{2}\:\:} \\ $$$$−\mathrm{2tan}^{−\mathrm{1}} \frac{\pi}{\mathrm{4}}=\mathrm{tan}\:\left(\theta_{\mathrm{1}} −\theta_{\mathrm{2}\:} \right) \\ $$$$\mathrm{2}.\frac{\pi}{\mathrm{4}}=\theta_{\mathrm{1}} −\theta_{\mathrm{2}} \\ $$$$\frac{\pi}{\mathrm{2}}=\theta_{\mathrm{1}} −\theta_{\mathrm{2}} \\ $$$${right}\:{or}\:{wrong}? \\ $$$$ \\ $$
Commented by Tawa1 last updated on 24/Dec/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by peter frank last updated on 24/Dec/18
[arg(z_1 +z_(2 ) )−arg(z_1 −z_2 )=(π/2) arg[(x_(1 ) +x_2 )+i(y_1 +y_2 )]−[arg(x_1 −x_2 +i(y_1 −y_2 )] tan^(−1) (((y_(1 ) +y_2 )/(x_1 +x_2 )))−tan^(−1) (((y_1 −y_2 )/(x_1 −x_2 )))=(π/2) (((y_(1 ) +y_2 )/(x_1 +x_2 )))+(((y_1 −y_2 )/(x_1 −x_2 )))÷[1−(((y_1 +y_2 )/(x_1 +x_2 ))).(((y_1 −y_2 )/(x_(1 ) −x_2 )))=(π/2) (((y_(1 ) +y_2 )/(x_1 +x_2 )))+(((y_1 −y_2 )/(x_1 −x_2 )))÷[1−(((y_1 +y_2 )/(x_1 +x_2 ))).(((y_1 −y_2 )/(x_(1 ) −x_2 )))=(1/0) x_1 ^2 −x_2 ^2 +y_2 ^2 −y_1 ^2 =0 x_1 ^2 +y_1 ^2 −x_2 ^2 −y_2 ^2 =0 x_1 ^2 +y_1 ^2 =x_2 ^2 +y_(2 ) ^2 ∣z_(1 ) ∣=∣z_2 ∣
$$\left[{arg}\left({z}_{\mathrm{1}} +{z}_{\mathrm{2}\:} \right)−{arg}\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)=\frac{\pi}{\mathrm{2}}\right. \\ $$$${arg}\left[\left({x}_{\mathrm{1}\:} +{x}_{\mathrm{2}} \right)+{i}\left({y}_{\mathrm{1}} +{y}_{\mathrm{2}} \right)\right]−\left[{arg}\left({x}_{\mathrm{1}} −{x}_{\mathrm{2}} +{i}\left({y}_{\mathrm{1}} −{y}_{\mathrm{2}} \right)\right]\right. \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{{y}_{\mathrm{1}\:} +{y}_{\mathrm{2}} }{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{{y}_{\mathrm{1}} −{y}_{\mathrm{2}} }{{x}_{\mathrm{1}} −{x}_{\mathrm{2}} }\right)=\frac{\pi}{\mathrm{2}} \\ $$$$\left(\frac{{y}_{\mathrm{1}\:} +{y}_{\mathrm{2}} }{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }\right)+\left(\frac{{y}_{\mathrm{1}} −{y}_{\mathrm{2}} }{{x}_{\mathrm{1}} −{x}_{\mathrm{2}} }\right)\boldsymbol{\div}\left[\mathrm{1}−\left(\frac{{y}_{\mathrm{1}} +{y}_{\mathrm{2}} }{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }\right).\left(\frac{{y}_{\mathrm{1}} −{y}_{\mathrm{2}} }{{x}_{\mathrm{1}\:} −{x}_{\mathrm{2}} }\right)=\frac{\pi}{\mathrm{2}}\right. \\ $$$$\left(\frac{{y}_{\mathrm{1}\:} +{y}_{\mathrm{2}} }{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }\right)+\left(\frac{{y}_{\mathrm{1}} −{y}_{\mathrm{2}} }{{x}_{\mathrm{1}} −{x}_{\mathrm{2}} }\right)\boldsymbol{\div}\left[\mathrm{1}−\left(\frac{{y}_{\mathrm{1}} +{y}_{\mathrm{2}} }{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }\right).\left(\frac{{y}_{\mathrm{1}} −{y}_{\mathrm{2}} }{{x}_{\mathrm{1}\:} −{x}_{\mathrm{2}} }\right)=\frac{\mathrm{1}}{\mathrm{0}}\right. \\ $$$$\:{x}_{\mathrm{1}} ^{\mathrm{2}} −{x}_{\mathrm{2}} ^{\mathrm{2}} +{y}_{\mathrm{2}} ^{\mathrm{2}} −{y}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} −{x}_{\mathrm{2}} ^{\mathrm{2}} −{y}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} ={x}_{\mathrm{2}} ^{\mathrm{2}} +{y}_{\mathrm{2}\:\:} ^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\mid{z}_{\mathrm{1}\:} \mid=\mid{z}_{\mathrm{2}} \mid \\ $$$$ \\ $$
Commented by Tawa1 last updated on 24/Dec/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *