Question Number 182279 by meetbhavsar25 last updated on 06/Dec/22
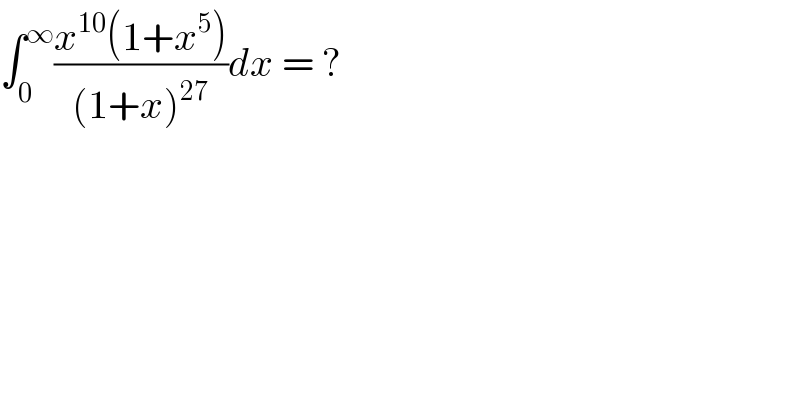
$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{10}} \left(\mathrm{1}+{x}^{\mathrm{5}} \right)}{\left(\mathrm{1}+{x}\right)^{\mathrm{27}} }{dx}\:=\:? \\ $$
Answered by Frix last updated on 07/Dec/22
![∫_0 ^∞ ((x^(10) (x^5 +1))/((x+1)^(27) ))dx=^(t=x+1) =∫_1 ^∞ ((1/t^(12) )−((15)/t^(13) )+((105)/t^(14) )−((455)/t^(15) )+((1365)/t^(16) )−((3002)/t^(17) )+((4995)/t^(18) )−((6390)/t^(19) )+((6315)/t^(20) )−((4795)/t^(21) )+((2751)/t^(22) )−((1155)/t^(23) )+((335)/t^(24) )−((60)/t^(25) )+(5/t^(26) ))dt= =−[(1/(11t^(11) ))−(5/(4t^(12) ))+((105)/(13t^(13) ))−((65)/(2t^(14) ))+((91)/t^(15) )−((1501)/(8t^(16) ))+((4995)/(17t^(17) ))−((355)/t^(18) )+((6315)/(19t^(19) ))−((959)/(4t^(20) ))+((131)/t^(21) )−((105)/(2t^(22) ))+((335)/(23t^(23) ))−(5/(2t^(24) ))+(1/(5t^(25) ))]_1 ^∞ = =(1/(42 493 880))](https://www.tinkutara.com/question/Q182290.png)
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{x}^{\mathrm{10}} \left({x}^{\mathrm{5}} +\mathrm{1}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{27}} }{dx}\overset{{t}={x}+\mathrm{1}} {=} \\ $$$$=\underset{\mathrm{1}} {\overset{\infty} {\int}}\left(\frac{\mathrm{1}}{{t}^{\mathrm{12}} }−\frac{\mathrm{15}}{{t}^{\mathrm{13}} }+\frac{\mathrm{105}}{{t}^{\mathrm{14}} }−\frac{\mathrm{455}}{{t}^{\mathrm{15}} }+\frac{\mathrm{1365}}{{t}^{\mathrm{16}} }−\frac{\mathrm{3002}}{{t}^{\mathrm{17}} }+\frac{\mathrm{4995}}{{t}^{\mathrm{18}} }−\frac{\mathrm{6390}}{{t}^{\mathrm{19}} }+\frac{\mathrm{6315}}{{t}^{\mathrm{20}} }−\frac{\mathrm{4795}}{{t}^{\mathrm{21}} }+\frac{\mathrm{2751}}{{t}^{\mathrm{22}} }−\frac{\mathrm{1155}}{{t}^{\mathrm{23}} }+\frac{\mathrm{335}}{{t}^{\mathrm{24}} }−\frac{\mathrm{60}}{{t}^{\mathrm{25}} }+\frac{\mathrm{5}}{{t}^{\mathrm{26}} }\right){dt}= \\ $$$$=−\left[\frac{\mathrm{1}}{\mathrm{11}{t}^{\mathrm{11}} }−\frac{\mathrm{5}}{\mathrm{4}{t}^{\mathrm{12}} }+\frac{\mathrm{105}}{\mathrm{13}{t}^{\mathrm{13}} }−\frac{\mathrm{65}}{\mathrm{2}{t}^{\mathrm{14}} }+\frac{\mathrm{91}}{{t}^{\mathrm{15}} }−\frac{\mathrm{1501}}{\mathrm{8}{t}^{\mathrm{16}} }+\frac{\mathrm{4995}}{\mathrm{17}{t}^{\mathrm{17}} }−\frac{\mathrm{355}}{{t}^{\mathrm{18}} }+\frac{\mathrm{6315}}{\mathrm{19}{t}^{\mathrm{19}} }−\frac{\mathrm{959}}{\mathrm{4}{t}^{\mathrm{20}} }+\frac{\mathrm{131}}{{t}^{\mathrm{21}} }−\frac{\mathrm{105}}{\mathrm{2}{t}^{\mathrm{22}} }+\frac{\mathrm{335}}{\mathrm{23}{t}^{\mathrm{23}} }−\frac{\mathrm{5}}{\mathrm{2}{t}^{\mathrm{24}} }+\frac{\mathrm{1}}{\mathrm{5}{t}^{\mathrm{25}} }\right]_{\mathrm{1}} ^{\infty} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{42}\:\mathrm{493}\:\mathrm{880}} \\ $$
