Question Number 182348 by mathlove last updated on 08/Dec/22
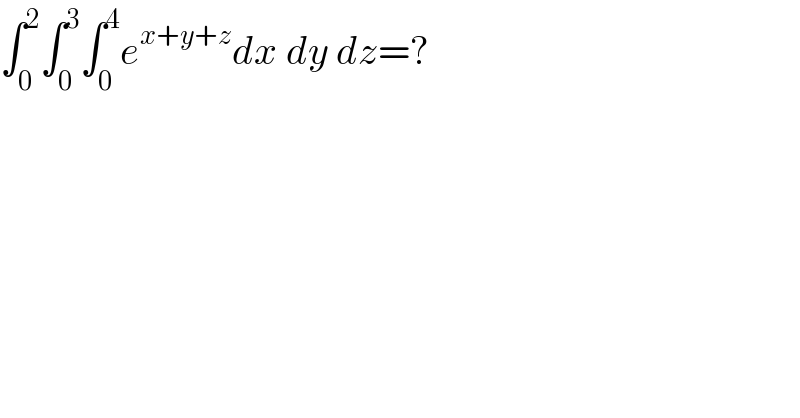
$$\int_{\mathrm{0}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{3}} \int_{\mathrm{0}} ^{\mathrm{4}} {e}^{{x}+{y}+{z}} {dx}\:{dy}\:{dz}=? \\ $$
Answered by CrispyXYZ last updated on 08/Dec/22

$$=\int_{\mathrm{0}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{3}} \left({e}^{\mathrm{4}} −\mathrm{1}\right){e}^{{y}+{z}} \:{dy}\:{dz} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \left({e}^{\mathrm{4}} −\mathrm{1}\right)\left({e}^{\mathrm{3}} −\mathrm{1}\right){e}^{{z}} \:{dz} \\ $$$$=\left({e}^{\mathrm{4}} −\mathrm{1}\right)\left({e}^{\mathrm{3}} −\mathrm{1}\right)\left({e}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\approx\mathrm{6535}.\mathrm{68} \\ $$
