Question Number 182360 by Rasheed.Sindhi last updated on 08/Dec/22

$$\mathrm{In}\:\mathrm{equation}\:\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}=\mathrm{0},\:\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{are} \\ $$$$\mathrm{randomly}\:\mathrm{selected}\:\mathrm{from}\:\mathrm{integers}; \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{roots} \\ $$$$\mathrm{will}\:\mathrm{be}\:\mathrm{real}? \\ $$
Commented by mr W last updated on 08/Dec/22

$${i}'{m}\:{not}\:{sure}\:{if}\:{there}\:{is}\:{a}\:{solution}. \\ $$$${but}\:{i}\:{think}\:{there}\:{is}\:{a}\:{solution}\:{when} \\ $$$${the}\:{question}\:{is}\:{e}.{g}.\:{like}\:{a},{b},{c}\:\in{R},\:{and}\: \\ $$$$\mathrm{0}\leqslant{a},{b},{c}\leqslant\mathrm{10}.\:{in}\:{this}\:{case}\:{we}\:{have} \\ $$$${p}=\frac{\mathrm{5}+\mathrm{6}\:\mathrm{ln}\:\mathrm{2}}{\mathrm{36}}\approx\mathrm{25}.\mathrm{4\%},\:{see}\:{below}.\:{please} \\ $$$${check}. \\ $$
Commented by mr W last updated on 08/Dec/22
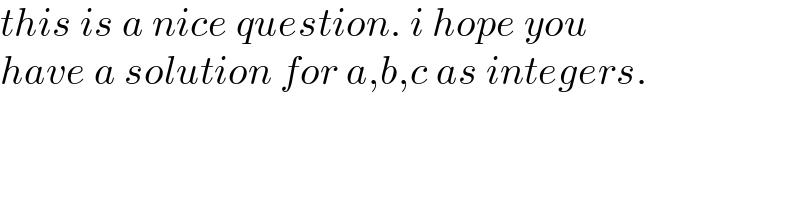
$${this}\:{is}\:{a}\:{nice}\:{question}.\:{i}\:{hope}\:{you} \\ $$$${have}\:{a}\:{solution}\:{for}\:{a},{b},{c}\:{as}\:{integers}. \\ $$
Commented by Rasheed.Sindhi last updated on 09/Dec/22

$${No}\:\boldsymbol{{sir}},{I}\:\:{know}\:{nothing}\:{about} \\ $$$${answer}/{solution}.{Actually}\:{it}'{s}\:{beyond} \\ $$$${my}\:{capacity}!\:{But}\:{only}\:{question} \\ $$$${raised}\:{in}\:{my}\:{mind}\:{and}\:{I}\:{threw} \\ $$$${it}\:{for}\:{discussion}. \\ $$
Commented by mr W last updated on 09/Dec/22

$${i}\:{see},\:{thanks}! \\ $$$${i}\:{think}\:{we}\:{can}'{t}\:{answer}\:{the}\:{question}, \\ $$$${if}\:{we}\:{don}'{t}\:{restrain}\:{the}\:{range}\:{of}\:{the} \\ $$$${values}.\:{that}'{s}\:{the}\:{same}\:{as}\:{we}\:{can}'{t} \\ $$$${determine}\:{the}\:{probability}\:{of}\:{drawing} \\ $$$${a}\:{black}\:{ball}\:{from}\:{a}\:{bag},\:{if}\:{we}\:{don}'{t}\: \\ $$$${know}\:{how}\:{many}\:{balls}\:{are}\:{in}\:{the}\:{bag} \\ $$$${or}\:{if}\:{the}\:{number}\:{of}\:{balls}\:{in}\:{the}\:{bag}\:{is} \\ $$$${infinite}.\:{an}\:{other}\:{issue}\:{is},\:{when}\: \\ $$$${a},{b},{c}\:{are}\:{integers}\:{in}\:{a}\:{given}\:{range}, \\ $$$${say}\:−\mathrm{10}\leqslant{a}\leqslant\mathrm{20},\:\mathrm{10}\leqslant{b}\leqslant\mathrm{50},\:−\mathrm{20}\leqslant{c}\leqslant\mathrm{0} \\ $$$${we}\:{can}\:{solve}\:{it},\:{but}\:{we}\:{have}\:{to}\:{check}\: \\ $$$${all}\:\mathrm{31}×\mathrm{41}×\mathrm{21}=\mathrm{26691}\:{discrete}\:{points}\: \\ $$$${one}\:{after}\:{one}\:{to}\:{see}\:{which}\:{points}\: \\ $$$${fulfill}\:\:{b}^{\mathrm{2}} \geqslant\mathrm{4}{ac}\:{and}\:{get}\:{the}\:{number}\: \\ $$$${of}\:{such}\:{points},\:{say}\:{n}_{\mathrm{1}} .\:{then}\:{we}\:{can}\: \\ $$$${calculate}\:{the}\:{probability}\:{p}=\frac{{n}_{\mathrm{1}} }{\mathrm{26691}}.\: \\ $$$${this}\:{is}\:{an}\:{easy}\:{but}\:{tough}\:{and}\:{stupid}\: \\ $$$${process}. \\ $$$${but}\:{when}\:{a},{b},{c}\:{are}\:{not}\:{discrete}\:{integer} \\ $$$${values},\:{but}\:{continuous}\:{real}\:{values}\:{in} \\ $$$${a}\:{given}\:{range},\:{we}\:{can}\:{apply}\:{functions} \\ $$$${and}\:{their}\:{integrals}\:{to}\:{find}\:{the} \\ $$$${probability}\:{as}\:{i}\:{showed}\:{below}. \\ $$$${any}\:{way},\:{thank}\:{you}\:{for}\:{creating}\:{a} \\ $$$${very}\:{interesting}\:{question}! \\ $$
Commented by Rasheed.Sindhi last updated on 09/Dec/22

$$\mathbb{G}\boldsymbol{\mathrm{rateful}}\:\boldsymbol{\mathrm{sir}},\:\mathrm{for}\:\mathrm{your}\:\boldsymbol{\mathrm{very}}\:\boldsymbol{\mathrm{deep}}\:\mathrm{disscussion} \\ $$$$\mathrm{and}\:\mathrm{for}\:\mathrm{your}\:\boldsymbol{\mathrm{very}}\:\boldsymbol{\mathrm{precious}}\:\mathrm{time}! \\ $$
Answered by mr W last updated on 09/Dec/22

$${say}\:{the}\:{question}\:{is}: \\ $$$${a},{b},{c}\:\in{R}\:{and}\:\mathrm{0}\leqslant{a},{b},{c}\leqslant\mathrm{10}. \\ $$$${we}\:{know}\:{the}\:{equation}\:{at}^{\mathrm{2}} +{bt}+{c}=\mathrm{0} \\ $$$${has}\:{real}\:{roots},\:{when}\:{b}^{\mathrm{2}} \geqslant\mathrm{4}{ac}. \\ $$$${let}\:{a}={x},\:{c}={y},\:{b}={z}. \\ $$$${each}\:{randomly}\:{selected}\:{values}\:{for} \\ $$$${a},{b},{c}\:{represent}\:{a}\:{point}\:{inside}\:{the}\:{cube} \\ $$$$\mathrm{10}×\mathrm{10}×\mathrm{10}.\:{the}\:{equation}\:{has}\:{real} \\ $$$${roots},\:{when}\:{the}\:{point}\:{lies}\:{inside}\:{the} \\ $$$${zone}\:{b}^{\mathrm{2}} \geqslant\mathrm{4}{ac},\:{i}.{e}.\:{z}^{\mathrm{2}} \geqslant\mathrm{4}{xy}.\:{that}'{s}\:{the} \\ $$$${hatched}\:{areas}\:{in}\:{the}\:{diagram}. \\ $$$${the}\:{probability}\:{that}\:{the}\:{roots}\:{are} \\ $$$${real}\:{is}\:{then} \\ $$$${p}=\frac{{volume}\:{of}\:{the}\:{zone}\:{z}^{\mathrm{2}} \geqslant\mathrm{4}{xy}}{{volume}\:{of}\:{the}\:{cube}} \\ $$
Commented by mr W last updated on 08/Dec/22

Commented by mr W last updated on 08/Dec/22
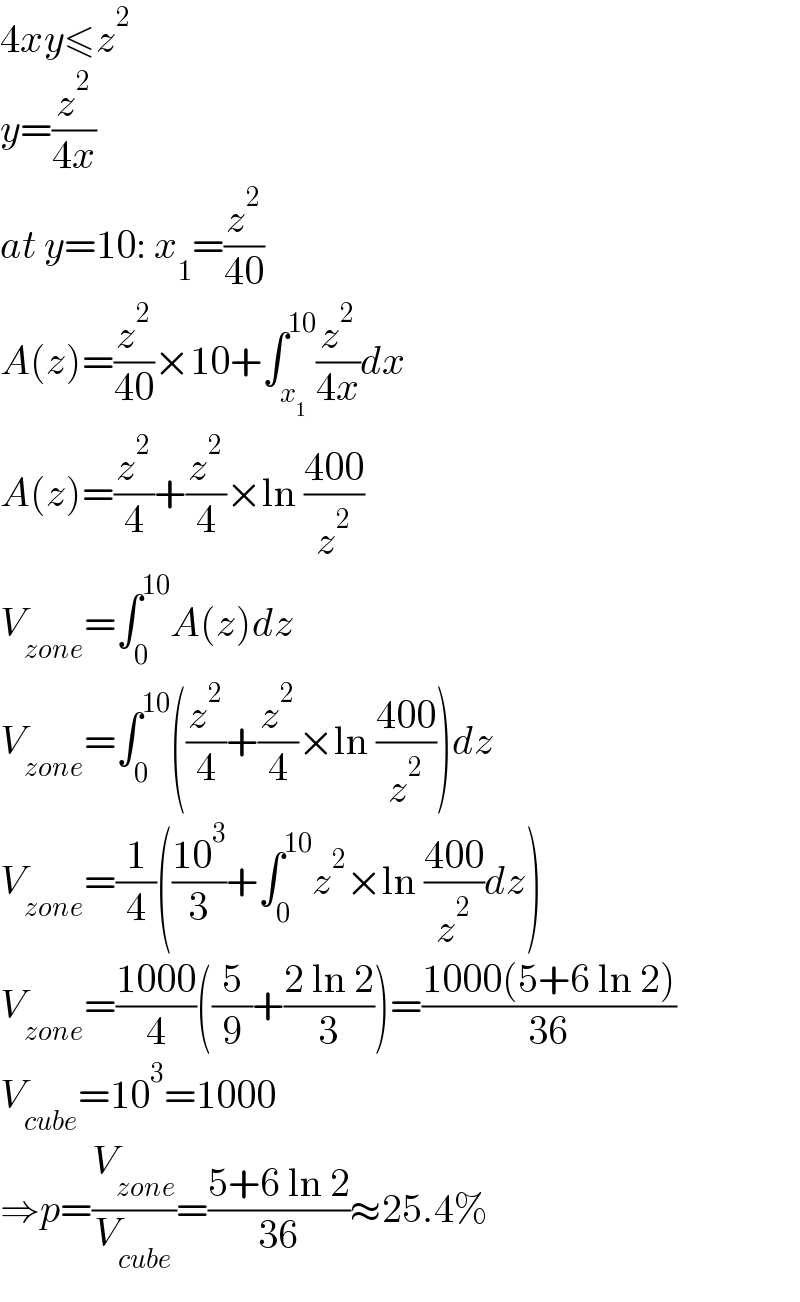
$$\mathrm{4}{xy}\leqslant{z}^{\mathrm{2}} \\ $$$${y}=\frac{{z}^{\mathrm{2}} }{\mathrm{4}{x}} \\ $$$${at}\:{y}=\mathrm{10}:\:{x}_{\mathrm{1}} =\frac{{z}^{\mathrm{2}} }{\mathrm{40}} \\ $$$${A}\left({z}\right)=\frac{{z}^{\mathrm{2}} }{\mathrm{40}}×\mathrm{10}+\int_{{x}_{\mathrm{1}} } ^{\mathrm{10}} \frac{{z}^{\mathrm{2}} }{\mathrm{4}{x}}{dx} \\ $$$${A}\left({z}\right)=\frac{{z}^{\mathrm{2}} }{\mathrm{4}}+\frac{{z}^{\mathrm{2}} }{\mathrm{4}}×\mathrm{ln}\:\frac{\mathrm{400}}{{z}^{\mathrm{2}} } \\ $$$${V}_{{zone}} =\int_{\mathrm{0}} ^{\mathrm{10}} {A}\left({z}\right){dz} \\ $$$${V}_{{zone}} =\int_{\mathrm{0}} ^{\mathrm{10}} \left(\frac{{z}^{\mathrm{2}} }{\mathrm{4}}+\frac{{z}^{\mathrm{2}} }{\mathrm{4}}×\mathrm{ln}\:\frac{\mathrm{400}}{{z}^{\mathrm{2}} }\right){dz} \\ $$$${V}_{{zone}} =\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{10}^{\mathrm{3}} }{\mathrm{3}}+\int_{\mathrm{0}} ^{\mathrm{10}} {z}^{\mathrm{2}} ×\mathrm{ln}\:\frac{\mathrm{400}}{{z}^{\mathrm{2}} }{dz}\right) \\ $$$${V}_{{zone}} =\frac{\mathrm{1000}}{\mathrm{4}}\left(\frac{\mathrm{5}}{\mathrm{9}}+\frac{\mathrm{2}\:\mathrm{ln}\:\mathrm{2}}{\mathrm{3}}\right)=\frac{\mathrm{1000}\left(\mathrm{5}+\mathrm{6}\:\mathrm{ln}\:\mathrm{2}\right)}{\mathrm{36}} \\ $$$${V}_{{cube}} =\mathrm{10}^{\mathrm{3}} =\mathrm{1000} \\ $$$$\Rightarrow{p}=\frac{{V}_{{zone}} }{{V}_{{cube}} }=\frac{\mathrm{5}+\mathrm{6}\:\mathrm{ln}\:\mathrm{2}}{\mathrm{36}}\approx\mathrm{25}.\mathrm{4\%} \\ $$
Commented by mr W last updated on 09/Dec/22
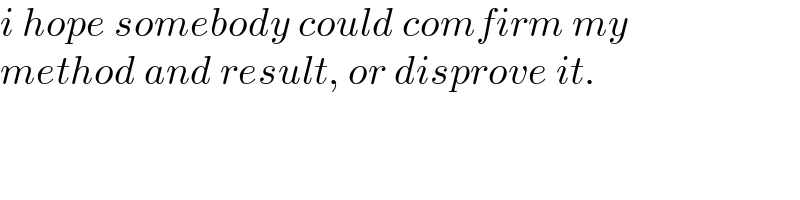
$${i}\:{hope}\:{somebody}\:{could}\:{comfirm}\:{my} \\ $$$${method}\:{and}\:{result},\:{or}\:{disprove}\:{it}. \\ $$
