Question Number 182375 by Acem last updated on 08/Dec/22

Commented by Acem last updated on 08/Dec/22
![I just solved it, 2 sec ago, φ ∈ ]20, 27[ Btw extend of NA intersects with extend of PC at point ∈ this circle Hope you success to find φ !](https://www.tinkutara.com/question/Q182381.png)
$$\:{I}\:{just}\:{solved}\:{it},\:\mathrm{2}\:{sec}\:{ago},\: \\ $$$$\left.\:\phi\:\in\:\right]\mathrm{20},\:\mathrm{27}\left[\right. \\ $$$$\:{Btw}\:{extend}\:{of}\:{NA}\:{intersects}\:{with}\:{extend}\:{of}\:{PC} \\ $$$$\:{at}\:{point}\:\in\:{this}\:{circle} \\ $$$$\:{Hope}\:{you}\:{success}\:{to}\:{find}\:\phi\:! \\ $$
Answered by mr W last updated on 08/Dec/22

Commented by Acem last updated on 08/Dec/22
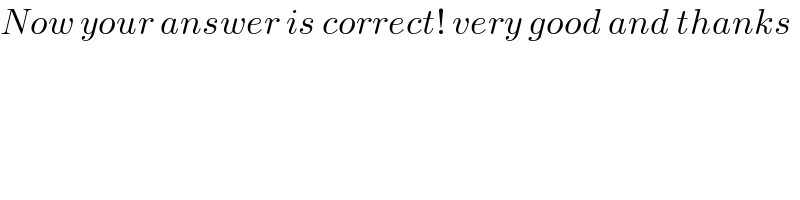
$${Now}\:{your}\:{answer}\:{is}\:{correct}!\:{very}\:{good}\:{and}\:{thanks} \\ $$
Commented by mr W last updated on 08/Dec/22
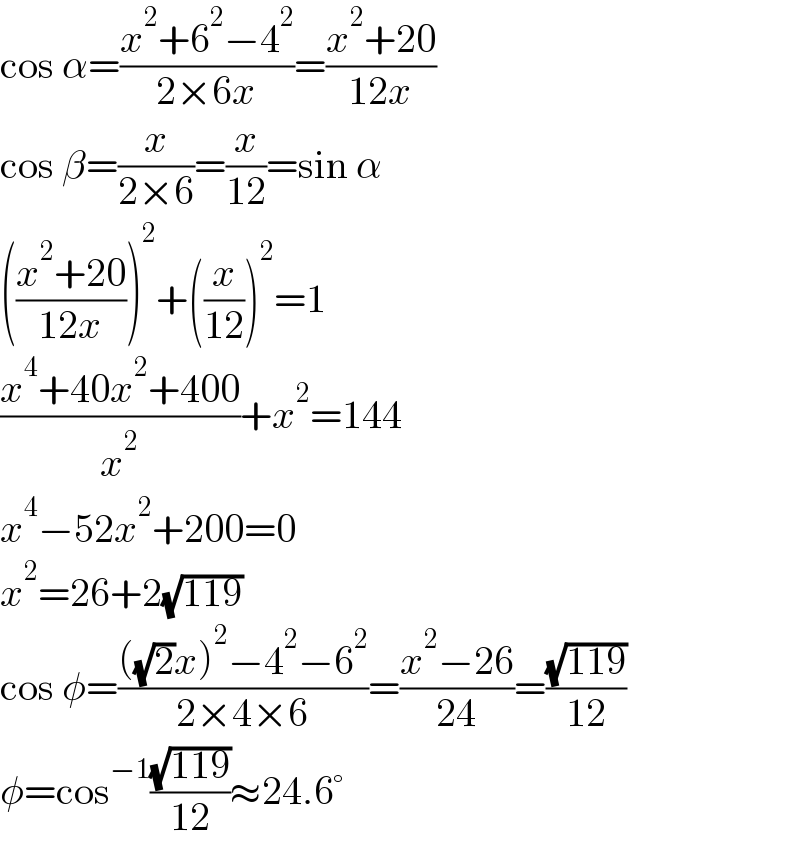
$$\mathrm{cos}\:\alpha=\frac{{x}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }{\mathrm{2}×\mathrm{6}{x}}=\frac{{x}^{\mathrm{2}} +\mathrm{20}}{\mathrm{12}{x}} \\ $$$$\mathrm{cos}\:\beta=\frac{{x}}{\mathrm{2}×\mathrm{6}}=\frac{{x}}{\mathrm{12}}=\mathrm{sin}\:\alpha \\ $$$$\left(\frac{{x}^{\mathrm{2}} +\mathrm{20}}{\mathrm{12}{x}}\right)^{\mathrm{2}} +\left(\frac{{x}}{\mathrm{12}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{4}} +\mathrm{40}{x}^{\mathrm{2}} +\mathrm{400}}{{x}^{\mathrm{2}} }+{x}^{\mathrm{2}} =\mathrm{144} \\ $$$${x}^{\mathrm{4}} −\mathrm{52}{x}^{\mathrm{2}} +\mathrm{200}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\mathrm{26}+\mathrm{2}\sqrt{\mathrm{119}} \\ $$$$\mathrm{cos}\:\phi=\frac{\left(\sqrt{\mathrm{2}}{x}\right)^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} −\mathrm{6}^{\mathrm{2}} }{\mathrm{2}×\mathrm{4}×\mathrm{6}}=\frac{{x}^{\mathrm{2}} −\mathrm{26}}{\mathrm{24}}=\frac{\sqrt{\mathrm{119}}}{\mathrm{12}} \\ $$$$\phi=\mathrm{cos}^{−\mathrm{1}} \frac{\sqrt{\mathrm{119}}}{\mathrm{12}}\approx\mathrm{24}.\mathrm{6}° \\ $$
Answered by Acem last updated on 08/Dec/22

