Question Number 182432 by SANOGO last updated on 09/Dec/22
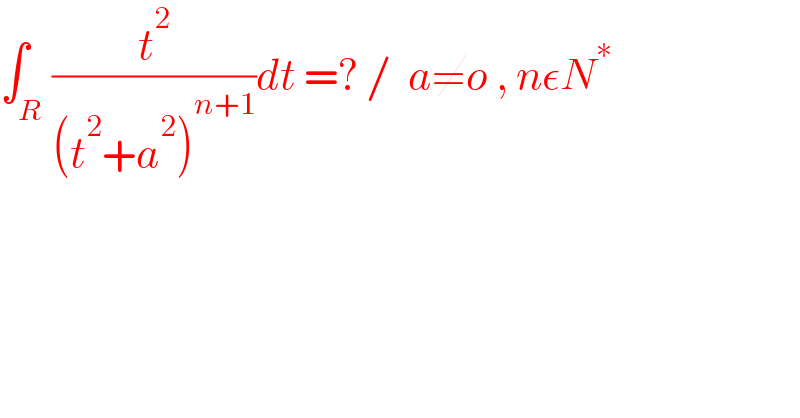
$$\int_{{R}} \frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{{n}+\mathrm{1}} }{dt}\:=?\:/\:\:{a}\neq{o}\:,\:{n}\epsilon{N}^{\ast} \\ $$
Answered by dre23 last updated on 10/Dec/22
![t=∣a∣s =∫_(−∞) ^∞ ((s^2 ∣a∣)/(a^(2n) (1+s^2 )^(n+1) ))ds,s=tg(z) =((2∣a∣)/a^(2n) )∫_0 ^(π/2) sin^2 (z)cos^(2n) (z)dz=A β(x,y)=2∫_0 ^(π/2) cos^(2x−1) (t)sin^(2y−1) (t)dt A=((∣a∣)/a^(2n) )β(2n+(1/2),1+(1/2))=((∣a∣)/a^(2n) ).((Γ(2n+(1/2))Γ(1+(1/2)))/(Γ(2n+2))) =((∣a∣[Π_(k=0) ^(2n−1) (k+(1/2))]Γ((1/2)).(1/2)Γ((1/2)))/(a^(2n) (2n+1)!)) =((π∣a∣Π_(k=0) ^n (2k+1))/(2^(2n+1) a^(2n) (2n+1)!))=((π∣a∣)/(2^(2n+1) a^(2n) 2^n n!)) =((π∣a∣)/(2^(3n+1) a^(2n) .n!))](https://www.tinkutara.com/question/Q182505.png)
$${t}=\mid{a}\mid{s} \\ $$$$=\int_{−\infty} ^{\infty} \frac{{s}^{\mathrm{2}} \mid{a}\mid}{{a}^{\mathrm{2}{n}} \left(\mathrm{1}+{s}^{\mathrm{2}} \right)^{{n}+\mathrm{1}} }{ds},{s}={tg}\left({z}\right) \\ $$$$=\frac{\mathrm{2}\mid{a}\mid}{{a}^{\mathrm{2}{n}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} \left({z}\right){cos}^{\mathrm{2}{n}} \left({z}\right){dz}=\boldsymbol{{A}} \\ $$$$\beta\left({x},{y}\right)=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}{x}−\mathrm{1}} \left({t}\right){sin}^{\mathrm{2}{y}−\mathrm{1}} \left(\boldsymbol{{t}}\right)\boldsymbol{{dt}} \\ $$$${A}=\frac{\mid{a}\mid}{{a}^{\mathrm{2}{n}} }\beta\left(\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mid{a}\mid}{{a}^{\mathrm{2}{n}} }.\frac{\Gamma\left(\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}{n}+\mathrm{2}\right)} \\ $$$$=\frac{\mid{a}\mid\left[\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\prod}}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right]\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right).\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{{a}^{\mathrm{2}{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$=\frac{\pi\mid{a}\mid\underset{{k}=\mathrm{0}} {\overset{{n}} {\prod}}\left(\mathrm{2}{k}+\mathrm{1}\right)}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} {a}^{\mathrm{2}{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)!}=\frac{\pi\mid{a}\mid}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} {a}^{\mathrm{2}{n}} \mathrm{2}^{{n}} {n}!} \\ $$$$=\frac{\pi\mid{a}\mid}{\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} {a}^{\mathrm{2}{n}} .{n}!} \\ $$$$ \\ $$
Commented by SANOGO last updated on 11/Dec/22
$${merci} \\ $$
Commented by dre23 last updated on 14/Dec/22

$${je}\:{vous}\:{en}\:{Prie} \\ $$
