Question Number 51364 by rahul 19 last updated on 26/Dec/18
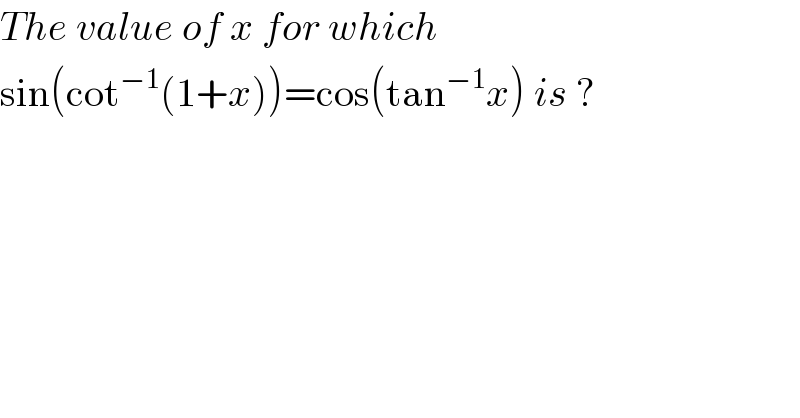
$${The}\:{value}\:{of}\:{x}\:{for}\:{which} \\ $$$$\mathrm{sin}\left(\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{1}+{x}\right)\right)=\mathrm{cos}\left(\mathrm{tan}^{−\mathrm{1}} {x}\right)\:{is}\:? \\ $$
Commented by rahul 19 last updated on 26/Dec/18
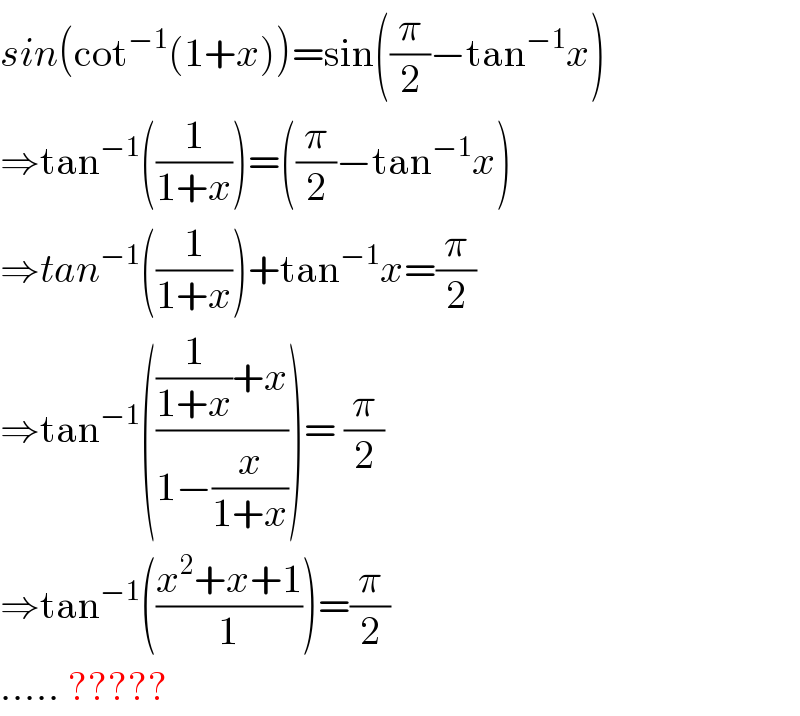
$${sin}\left(\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{1}+{x}\right)\right)=\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} {x}\right) \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}+{x}}\right)=\left(\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} {x}\right) \\ $$$$\Rightarrow{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}+{x}}\right)+\mathrm{tan}^{−\mathrm{1}} {x}=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{1}}{\mathrm{1}+{x}}+{x}}{\mathrm{1}−\frac{{x}}{\mathrm{1}+{x}}}\right)=\:\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{\mathrm{1}}\right)=\frac{\pi}{\mathrm{2}} \\ $$$$…..\:????? \\ $$
Commented by prakash jain last updated on 26/Dec/18
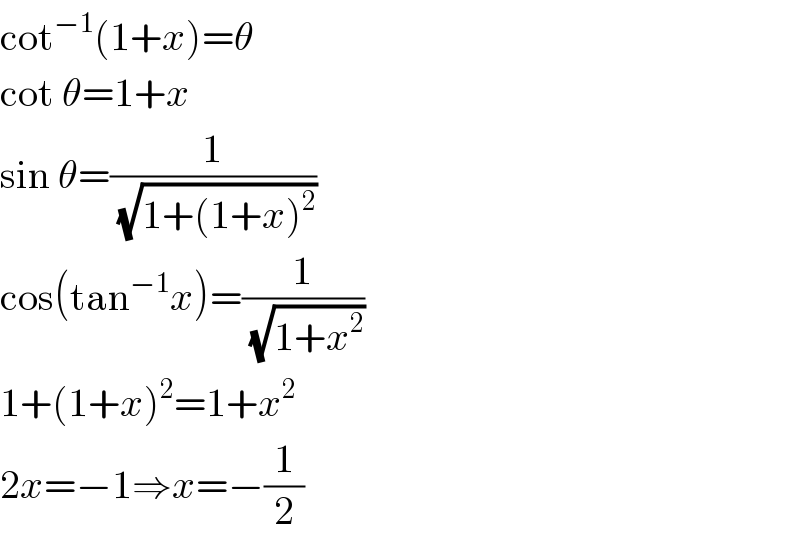
$$\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{1}+{x}\right)=\theta \\ $$$$\mathrm{cot}\:\theta=\mathrm{1}+{x} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\left(\mathrm{tan}^{−\mathrm{1}} {x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$\mathrm{1}+\left(\mathrm{1}+{x}\right)^{\mathrm{2}} =\mathrm{1}+{x}^{\mathrm{2}} \\ $$$$\mathrm{2}{x}=−\mathrm{1}\Rightarrow{x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
