Question Number 182453 by universe last updated on 09/Dec/22
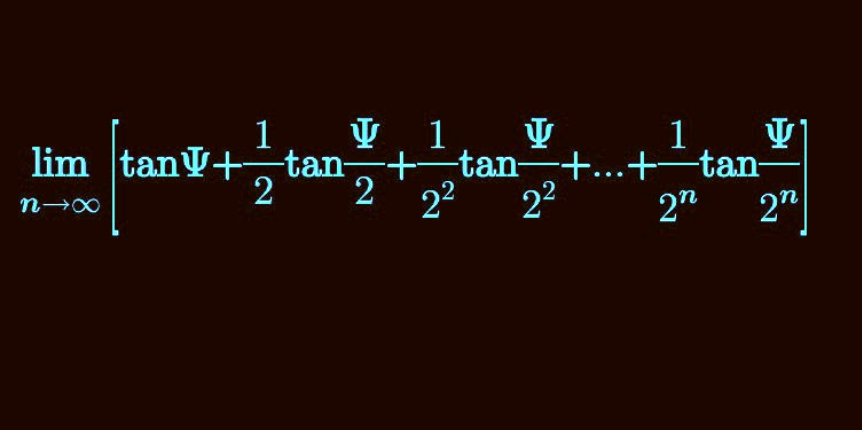
Answered by qaz last updated on 10/Dec/22
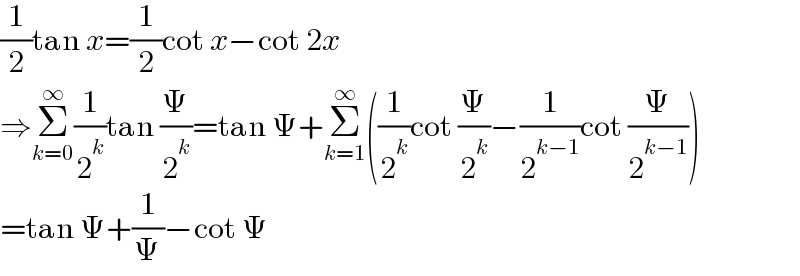
$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cot}\:{x}−\mathrm{cot}\:\mathrm{2}{x} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\mathrm{tan}\:\frac{\Psi}{\mathrm{2}^{{k}} }=\mathrm{tan}\:\Psi+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\mathrm{cot}\:\frac{\Psi}{\mathrm{2}^{{k}} }−\frac{\mathrm{1}}{\mathrm{2}^{{k}−\mathrm{1}} }\mathrm{cot}\:\frac{\Psi}{\mathrm{2}^{{k}−\mathrm{1}} }\right) \\ $$$$=\mathrm{tan}\:\Psi+\frac{\mathrm{1}}{\Psi}−\mathrm{cot}\:\Psi \\ $$
