Menu Close

How-many-5-digits-positive-integers-x-1-x-2-x-3-x-4-x-5-are-there-such-that-x-1-x-2-x-3-x-4-x-5-

Tinku Tara 0 Comments
Pin




Question Number 117061 by ZiYangLee last updated on 09/Oct/20
How many 5-digits positive integers x_1 x_2 x_3 x_4 x_5 are there such that x_1 ≤x_2 ≤x_3 ≤x_4 ≤x_5 ?
$$\mathrm{How}\:\mathrm{many}\:\mathrm{5}-\mathrm{digits}\:\mathrm{positive}\:\mathrm{integers} \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} {x}_{\mathrm{4}} {x}_{\mathrm{5}} \:\mathrm{are}\:\mathrm{there}\:\mathrm{such}\:\mathrm{that}\: \\ $$$${x}_{\mathrm{1}} \leqslant{x}_{\mathrm{2}} \leqslant{x}_{\mathrm{3}} \leqslant{x}_{\mathrm{4}} \leqslant{x}_{\mathrm{5}} ? \\ $$
Commented by ZiYangLee last updated on 09/Oct/20
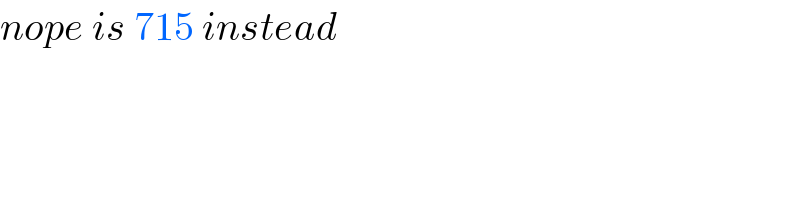
nope is 715 instead
$${nope}\:{is}\:\mathrm{715}\:{instead} \\ $$
Commented by MJS_new last updated on 09/Oct/20
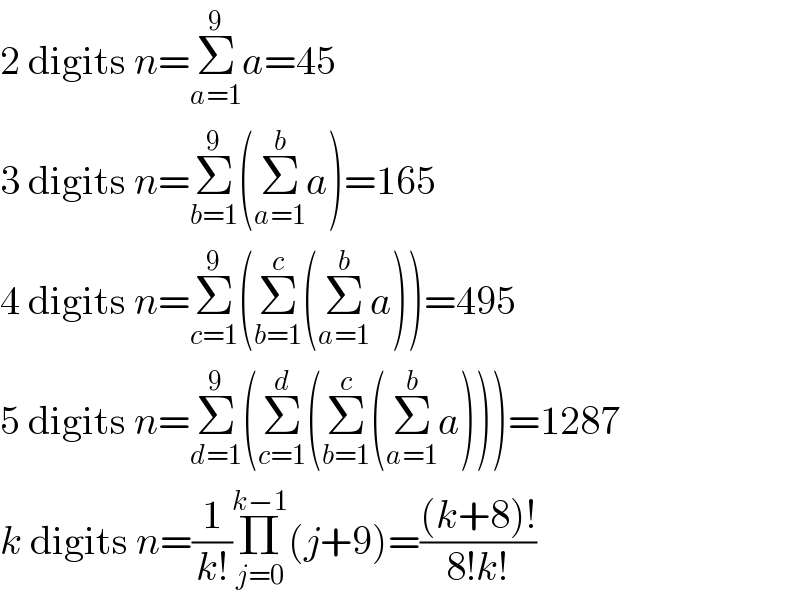
2 digits n=Σ_(a=1) ^9 a=45 3 digits n=Σ_(b=1) ^9 (Σ_(a=1) ^b a)=165 4 digits n=Σ_(c=1) ^9 (Σ_(b=1) ^c (Σ_(a=1) ^b a))=495 5 digits n=Σ_(d=1) ^9 (Σ_(c=1) ^d (Σ_(b=1) ^c (Σ_(a=1) ^b a)))=1287 k digits n=(1/(k!))Π_(j=0) ^(k−1) (j+9)=(((k+8)!)/(8!k!))
$$\mathrm{2}\:\mathrm{digits}\:{n}=\underset{{a}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}{a}=\mathrm{45} \\ $$$$\mathrm{3}\:\mathrm{digits}\:{n}=\underset{{b}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left(\underset{{a}=\mathrm{1}} {\overset{{b}} {\sum}}{a}\right)=\mathrm{165} \\ $$$$\mathrm{4}\:\mathrm{digits}\:{n}=\underset{{c}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left(\underset{{b}=\mathrm{1}} {\overset{{c}} {\sum}}\left(\underset{{a}=\mathrm{1}} {\overset{{b}} {\sum}}{a}\right)\right)=\mathrm{495} \\ $$$$\mathrm{5}\:\mathrm{digits}\:{n}=\underset{{d}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left(\underset{{c}=\mathrm{1}} {\overset{{d}} {\sum}}\left(\underset{{b}=\mathrm{1}} {\overset{{c}} {\sum}}\left(\underset{{a}=\mathrm{1}} {\overset{{b}} {\sum}}{a}\right)\right)\right)=\mathrm{1287} \\ $$$${k}\:\mathrm{digits}\:{n}=\frac{\mathrm{1}}{{k}!}\underset{{j}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\left({j}+\mathrm{9}\right)=\frac{\left({k}+\mathrm{8}\right)!}{\mathrm{8}!{k}!} \\ $$
Commented by MJS_new last updated on 09/Oct/20
how you get 715?
$$\mathrm{how}\:\mathrm{you}\:\mathrm{get}\:\mathrm{715}? \\ $$
Answered by Olaf last updated on 09/Oct/20
A number is a plaindrome in a given base b (often 10 or 16) if its digits are in nondecreasing order in that base. A plaindrome in which the digits are strictly increasing is called metadrome, while numbers whose digits are nonincreasing and strictly decreasing are called nialpdromes and katadromes. See OEIS, Sequence A009994 (base 10) See OEIS, Sequence A023757 (base 16) See numbersaplenty.com for calculous. (in english) See villemin.gerard.free.fr (but this is in french)
$$\mathrm{A}\:\mathrm{number}\:\mathrm{is}\:\mathrm{a}\:\mathrm{plaindrome}\:\mathrm{in}\:\mathrm{a}\:\mathrm{given} \\ $$$$\mathrm{base}\:{b}\:\left(\mathrm{often}\:\mathrm{10}\:\mathrm{or}\:\mathrm{16}\right)\:\mathrm{if}\:\mathrm{its}\:\mathrm{digits}\:\mathrm{are} \\ $$$$\mathrm{in}\:\mathrm{nondecreasing}\:\mathrm{order}\:\mathrm{in}\:\mathrm{that}\:\mathrm{base}. \\ $$$$\mathrm{A}\:\mathrm{plaindrome}\:\mathrm{in}\:\mathrm{which}\:\mathrm{the}\:\mathrm{digits}\:\mathrm{are} \\ $$$$\mathrm{strictly}\:\mathrm{increasing}\:\mathrm{is}\:\mathrm{called}\:\mathrm{metadrome}, \\ $$$$\mathrm{while}\:\mathrm{numbers}\:\mathrm{whose}\:\mathrm{digits}\:\mathrm{are}\: \\ $$$$\mathrm{nonincreasing}\:\mathrm{and}\:\mathrm{strictly}\:\mathrm{decreasing} \\ $$$$\mathrm{are}\:\mathrm{called}\:\mathrm{nialpdromes}\:\mathrm{and}\:\mathrm{katadromes}. \\ $$$$ \\ $$$$\mathrm{See}\:\mathrm{OEIS},\:\mathrm{Sequence}\:\mathrm{A009994}\:\left(\mathrm{base}\:\mathrm{10}\right) \\ $$$$\mathrm{See}\:\mathrm{OEIS},\:\mathrm{Sequence}\:\mathrm{A023757}\:\left(\mathrm{base}\:\mathrm{16}\right) \\ $$$$ \\ $$$$\mathrm{See}\:\mathrm{numbersaplenty}.\mathrm{com}\:\mathrm{for}\:\mathrm{calculous}. \\ $$$$\left(\mathrm{in}\:\mathrm{english}\right) \\ $$$$ \\ $$$$\mathrm{See}\:\mathrm{villemin}.\mathrm{gerard}.\mathrm{free}.\mathrm{fr} \\ $$$$\left(\mathrm{but}\:\mathrm{this}\:\mathrm{is}\:\mathrm{in}\:\mathrm{french}\right) \\ $$$$ \\ $$
Answered by mr W last updated on 11/Oct/20
we see in such a 5 digit number the digit zero is not allowed. so we can only select from digits 1 to 9. say the number of digit 1 is n_1 , the number of digit 2 is n_2 , etc. n_1 +n_2 +n_3 +...+n_9 =5 ...(i) with 0≤n_1 ,n_2 ,...,n_9 ≤5 we know that we can always arrange the n_1 times 1, n_2 times 2, ..., n_9 times 9 in increasing order to form a 5 digit number x_1 x_2 ...x_5 such that x_1 ≤x_2 ≤...≤x_5 . so the number of non−negative integer solutions of eqn. (i) is the answer of our question. the number of non−negative integer solutions of eqn. (i) is the coefficient of term x^5 of the following generating function (1+x+x^2 +x^3 +...)^9 =(1/((1−x)^9 ))=Σ_(k=0) ^∞ C_8 ^(k+8) x^k the cof. of x^5 term is C_8 ^(13) =1287. generally the number of k digit numbers is C_8 ^(k+8) =(((k+8)!)/(8!k!)).
$${we}\:{see}\:{in}\:{such}\:{a}\:\mathrm{5}\:{digit}\:{number}\:{the} \\ $$$${digit}\:{zero}\:{is}\:{not}\:{allowed}.\:{so}\:{we}\:{can} \\ $$$${only}\:{select}\:{from}\:{digits}\:\mathrm{1}\:{to}\:\mathrm{9}. \\ $$$${say}\:{the}\:{number}\:{of}\:{digit}\:\mathrm{1}\:{is}\:{n}_{\mathrm{1}} ,\:{the} \\ $$$${number}\:{of}\:{digit}\:\mathrm{2}\:{is}\:{n}_{\mathrm{2}} ,\:{etc}. \\ $$$${n}_{\mathrm{1}} +{n}_{\mathrm{2}} +{n}_{\mathrm{3}} +…+{n}_{\mathrm{9}} =\mathrm{5}\:\:\:…\left({i}\right) \\ $$$${with}\:\mathrm{0}\leqslant{n}_{\mathrm{1}} ,{n}_{\mathrm{2}} ,…,{n}_{\mathrm{9}} \leqslant\mathrm{5} \\ $$$${we}\:{know}\:{that}\:{we}\:{can}\:{always}\:{arrange} \\ $$$${the}\:{n}_{\mathrm{1}} \:{times}\:\mathrm{1},\:{n}_{\mathrm{2}} \:{times}\:\mathrm{2},\:…,\:{n}_{\mathrm{9}} \:{times} \\ $$$$\mathrm{9}\:{in}\:{increasing}\:{order}\:{to}\:{form}\:{a}\:\mathrm{5} \\ $$$${digit}\:{number}\:{x}_{\mathrm{1}} {x}_{\mathrm{2}} …{x}_{\mathrm{5}} \:{such}\:{that} \\ $$$${x}_{\mathrm{1}} \leqslant{x}_{\mathrm{2}} \leqslant…\leqslant{x}_{\mathrm{5}} . \\ $$$${so}\:{the}\:{number}\:{of}\:{non}−{negative} \\ $$$${integer}\:{solutions}\:{of}\:{eqn}.\:\left({i}\right)\:{is}\:{the} \\ $$$${answer}\:{of}\:{our}\:{question}. \\ $$$${the}\:{number}\:{of}\:{non}−{negative}\: \\ $$$${integer}\:{solutions}\:{of}\:{eqn}.\:\left({i}\right)\:{is}\:{the} \\ $$$${coefficient}\:{of}\:{term}\:{x}^{\mathrm{5}} \:{of}\:{the}\:{following} \\ $$$${generating}\:{function} \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…\right)^{\mathrm{9}} =\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{9}} }=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{8}} ^{{k}+\mathrm{8}} {x}^{{k}} \\ $$$${the}\:{cof}.\:{of}\:{x}^{\mathrm{5}} \:{term}\:{is}\:{C}_{\mathrm{8}} ^{\mathrm{13}} =\mathrm{1287}. \\ $$$$ \\ $$$${generally}\:{the}\:{number}\:{of}\:{k}\:{digit} \\ $$$${numbers}\:{is}\:{C}_{\mathrm{8}} ^{{k}+\mathrm{8}} =\frac{\left({k}+\mathrm{8}\right)!}{\mathrm{8}!{k}!}. \\ $$
Commented by mr W last updated on 11/Oct/20

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *