Question Number 117086 by mnjuly1970 last updated on 09/Oct/20
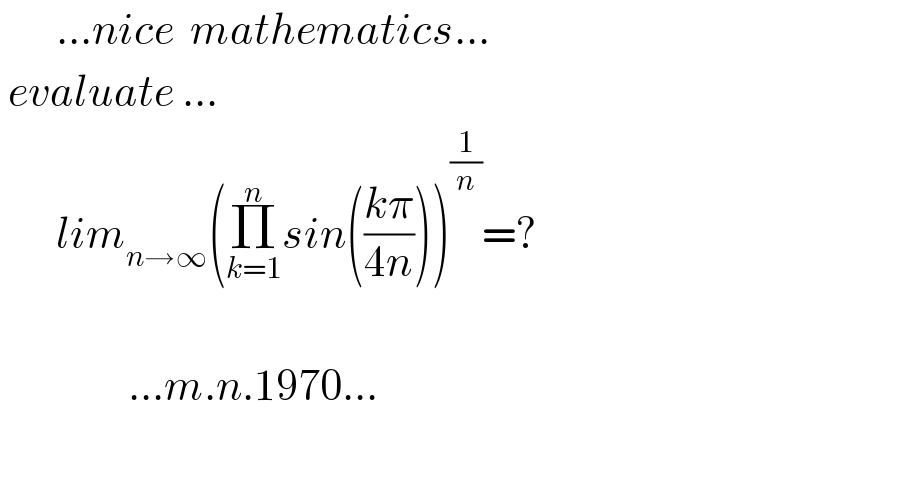
$$\:\:\:\:\:\:\:…{nice}\:\:{mathematics}… \\ $$$$\:{evaluate}\:… \\ $$$$\:\:\:\:\:\:\:{lim}_{{n}\rightarrow\infty} \left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{sin}\left(\frac{{k}\pi}{\mathrm{4}{n}}\right)\right)^{\frac{\mathrm{1}}{{n}}} =? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{m}.{n}.\mathrm{1970}… \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 09/Oct/20
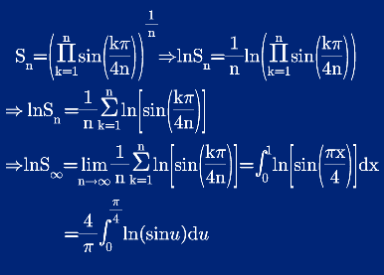
Commented by mnjuly1970 last updated on 09/Oct/20
$${thank}\:{you}\:{very}\:{much}.. \\ $$
Commented by Ar Brandon last updated on 09/Oct/20
You're welcome Sir ��
Answered by Dwaipayan Shikari last updated on 09/Oct/20
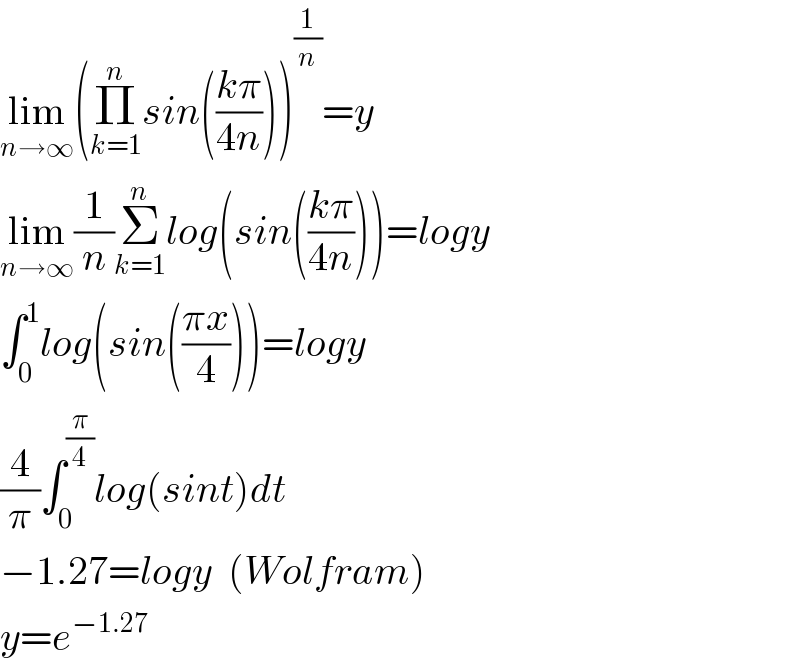
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{sin}\left(\frac{{k}\pi}{\mathrm{4}{n}}\right)\right)^{\frac{\mathrm{1}}{{n}}} ={y} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{log}\left({sin}\left(\frac{{k}\pi}{\mathrm{4}{n}}\right)\right)={logy} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left({sin}\left(\frac{\pi{x}}{\mathrm{4}}\right)\right)={logy} \\ $$$$\frac{\mathrm{4}}{\pi}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left({sint}\right){dt} \\ $$$$−\mathrm{1}.\mathrm{27}={logy}\:\:\left({Wolfram}\right) \\ $$$${y}={e}^{−\mathrm{1}.\mathrm{27}} \\ $$
Commented by Olaf last updated on 10/Oct/20
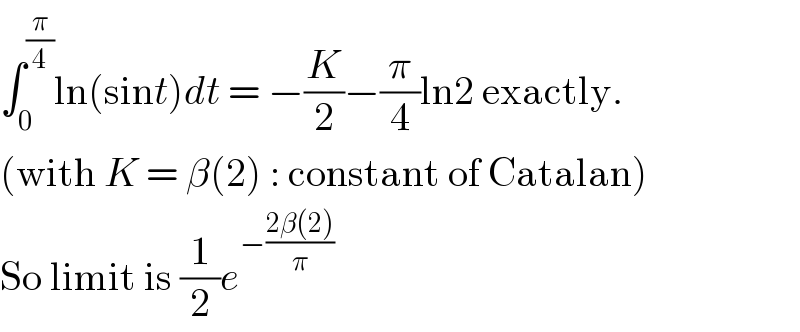
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{sin}{t}\right){dt}\:=\:−\frac{{K}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\mathrm{ln2}\:\mathrm{exactly}. \\ $$$$\left(\mathrm{with}\:{K}\:=\:\beta\left(\mathrm{2}\right)\::\:\mathrm{constant}\:\mathrm{of}\:\mathrm{Catalan}\right) \\ $$$$\mathrm{So}\:\mathrm{limit}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\frac{\mathrm{2}\beta\left(\mathrm{2}\right)}{\pi}} \\ $$
Commented by mnjuly1970 last updated on 09/Oct/20
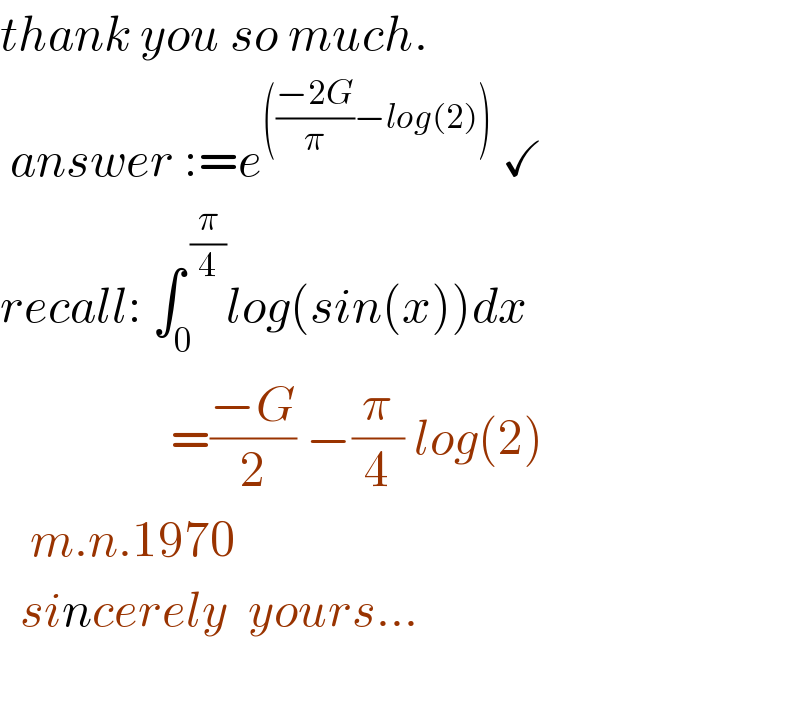
$${thank}\:{you}\:{so}\:{much}. \\ $$$$\:{answer}\::={e}^{\left(\frac{−\mathrm{2}{G}}{\pi}−{log}\left(\mathrm{2}\right)\right)} \:\checkmark \\ $$$${recall}:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {log}\left({sin}\left({x}\right)\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{−{G}}{\mathrm{2}}\:−\frac{\pi}{\mathrm{4}}\:{log}\left(\mathrm{2}\right) \\ $$$$\:\:\:{m}.{n}.\mathrm{1970} \\ $$$$\:\:{sincerely}\:\:{yours}… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by mnjuly1970 last updated on 10/Oct/20
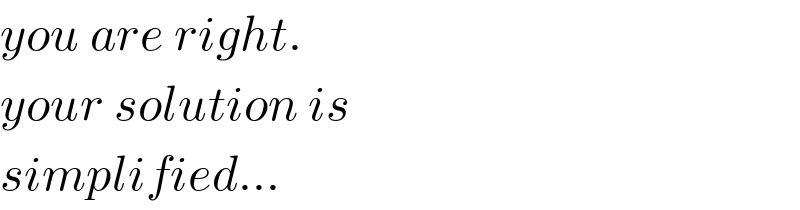
$${you}\:{are}\:{right}. \\ $$$${your}\:{solution}\:{is} \\ $$$${simplified}… \\ $$
