Question Number 117100 by bemath last updated on 09/Oct/20
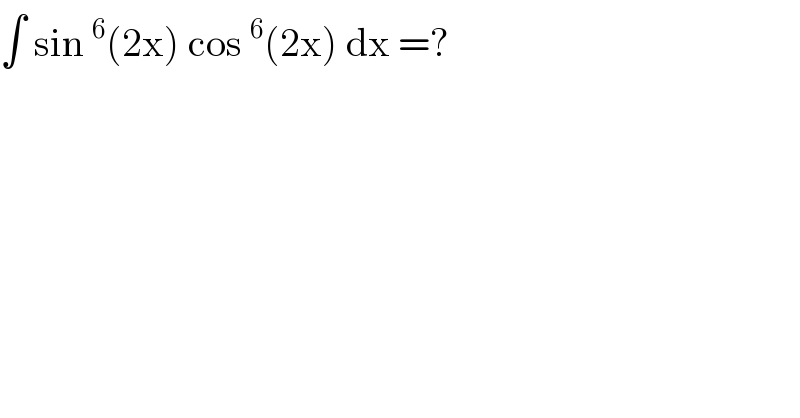
$$\int\:\mathrm{sin}\:^{\mathrm{6}} \left(\mathrm{2x}\right)\:\mathrm{cos}\:^{\mathrm{6}} \left(\mathrm{2x}\right)\:\mathrm{dx}\:=? \\ $$
Answered by Dwaipayan Shikari last updated on 09/Oct/20
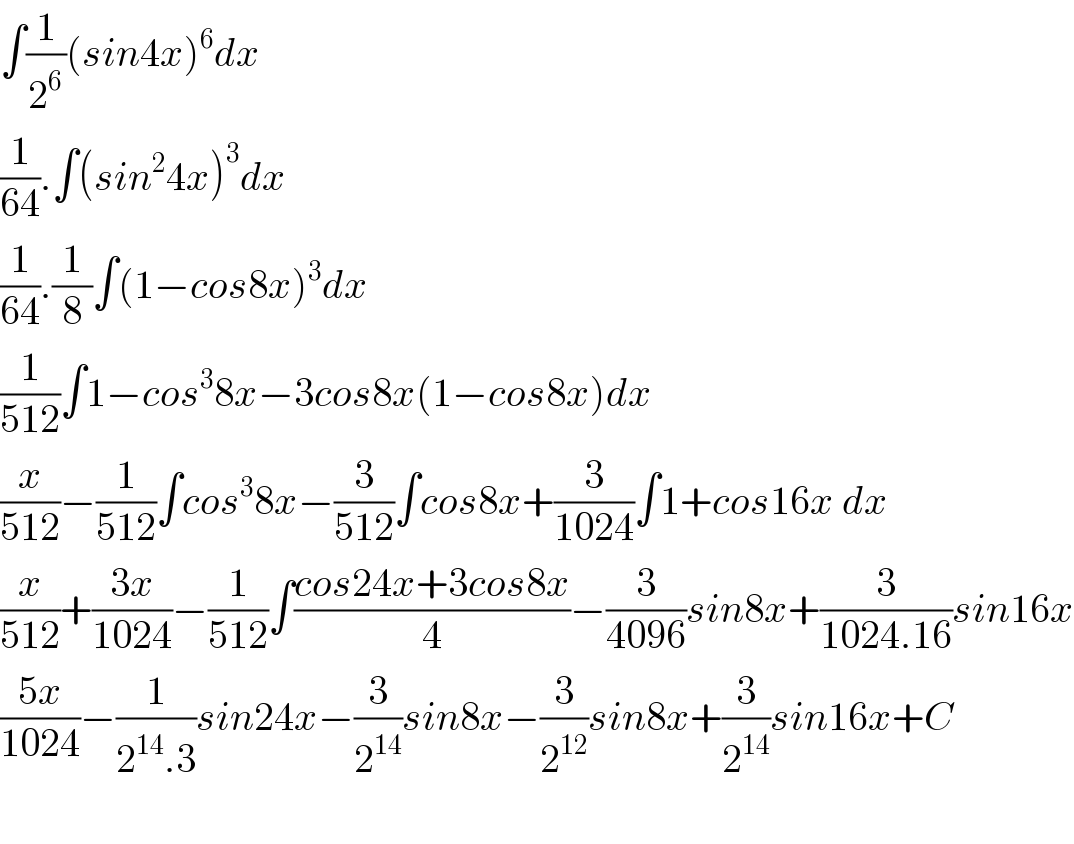
$$\int\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{6}} }\left({sin}\mathrm{4}{x}\right)^{\mathrm{6}} {dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{64}}.\int\left({sin}^{\mathrm{2}} \mathrm{4}{x}\right)^{\mathrm{3}} {dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{64}}.\frac{\mathrm{1}}{\mathrm{8}}\int\left(\mathrm{1}−{cos}\mathrm{8}{x}\right)^{\mathrm{3}} {dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{512}}\int\mathrm{1}−{cos}^{\mathrm{3}} \mathrm{8}{x}−\mathrm{3}{cos}\mathrm{8}{x}\left(\mathrm{1}−{cos}\mathrm{8}{x}\right){dx} \\ $$$$\frac{{x}}{\mathrm{512}}−\frac{\mathrm{1}}{\mathrm{512}}\int{cos}^{\mathrm{3}} \mathrm{8}{x}−\frac{\mathrm{3}}{\mathrm{512}}\int{cos}\mathrm{8}{x}+\frac{\mathrm{3}}{\mathrm{1024}}\int\mathrm{1}+{cos}\mathrm{16}{x}\:{dx} \\ $$$$\frac{{x}}{\mathrm{512}}+\frac{\mathrm{3}{x}}{\mathrm{1024}}−\frac{\mathrm{1}}{\mathrm{512}}\int\frac{{cos}\mathrm{24}{x}+\mathrm{3}{cos}\mathrm{8}{x}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{4096}}{sin}\mathrm{8}{x}+\frac{\mathrm{3}}{\mathrm{1024}.\mathrm{16}}{sin}\mathrm{16}{x} \\ $$$$\frac{\mathrm{5}{x}}{\mathrm{1024}}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{14}} .\mathrm{3}}{sin}\mathrm{24}{x}−\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{14}} }{sin}\mathrm{8}{x}−\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{12}} }{sin}\mathrm{8}{x}+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{14}} }{sin}\mathrm{16}{x}+{C} \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 09/Oct/20
![F=∫ sin^6 (2x) cos^6 (2x) dx = =(1/(64))∫[2sin(2x)cos(2x)]^6 dx =(1/(64))∫sin^6 (4x)dx= _(put 4x=t) (1/(256))∫sin^6 tdt =(1/(256)).(1/8)∫(1−cos2t)^3 dt =(1/2^(11) )∫(1−3cos2t+3cos^2 2t−cos^3 2t)dt =(1/2^(11) )[∫dt−(3/2)∫cos(2t)d(2t)+(3/2)∫(1+cos(4t))dt] −(1/2^(11) ).(1/2)∫(1−sin^2 2t)d(sin2t)) =(1/2^(11) )[t−(3/2)sin2t+(3/2)t+(3/8)sin4t] −(1/2^(12) )(sin2t−((sin^3 2t)/3)) =(5/2^(12) ) (4x)−(3/2^(12) )sin8x+(3/2^(14) )sin(16x) −(1/2^(12) )sin8t+(1/2^(12) )sin^3 8t =((5x)/2^(10) )−(1/2^(10) )sin8x+(1/2^(12) )sin^3 8x+(3/2^(14) )sin16x+C](https://www.tinkutara.com/question/Q117110.png)
$$\mathrm{F}=\int\:\mathrm{sin}\:^{\mathrm{6}} \left(\mathrm{2x}\right)\:\mathrm{cos}\:^{\mathrm{6}} \left(\mathrm{2x}\right)\:\mathrm{dx}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}\int\left[\mathrm{2sin}\left(\mathrm{2x}\right)\mathrm{cos}\left(\mathrm{2x}\right)\right]^{\mathrm{6}} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}\int\mathrm{sin}^{\mathrm{6}} \left(\mathrm{4x}\right)\mathrm{d}\underset{\mathrm{put}\:\mathrm{4x}=\mathrm{t}} {\mathrm{x}=\:\:\:}\frac{\mathrm{1}}{\mathrm{256}}\int\mathrm{sin}^{\mathrm{6}} \mathrm{tdt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{256}}.\frac{\mathrm{1}}{\mathrm{8}}\int\left(\mathrm{1}−\mathrm{cos2t}\right)^{\mathrm{3}} \mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{11}} }\int\left(\mathrm{1}−\mathrm{3cos2t}+\mathrm{3cos}^{\mathrm{2}} \mathrm{2t}−\mathrm{cos}^{\mathrm{3}} \mathrm{2t}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{11}} }\left[\int\mathrm{dt}−\frac{\mathrm{3}}{\mathrm{2}}\int\mathrm{cos}\left(\mathrm{2t}\right)\mathrm{d}\left(\mathrm{2t}\right)+\frac{\mathrm{3}}{\mathrm{2}}\int\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{4t}\right)\right)\mathrm{dt}\right] \\ $$$$\left.−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{11}} }.\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{2t}\right)\mathrm{d}\left(\mathrm{sin2t}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{11}} }\left[\mathrm{t}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{sin2t}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{t}+\frac{\mathrm{3}}{\mathrm{8}}\mathrm{sin4t}\right] \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{12}} }\left(\mathrm{sin2t}−\frac{\mathrm{sin}^{\mathrm{3}} \mathrm{2t}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{12}} }\:\left(\mathrm{4x}\right)−\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{12}} }\mathrm{sin8x}+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{14}} }\mathrm{sin}\left(\mathrm{16x}\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{12}} }\mathrm{sin8t}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{12}} }\mathrm{sin}^{\mathrm{3}} \mathrm{8t} \\ $$$$=\frac{\mathrm{5x}}{\mathrm{2}^{\mathrm{10}} }−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\mathrm{sin8x}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{12}} }\mathrm{sin}^{\mathrm{3}} \mathrm{8x}+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{14}} }\mathrm{sin16x}+\mathrm{C} \\ $$
Answered by Bird last updated on 10/Oct/20
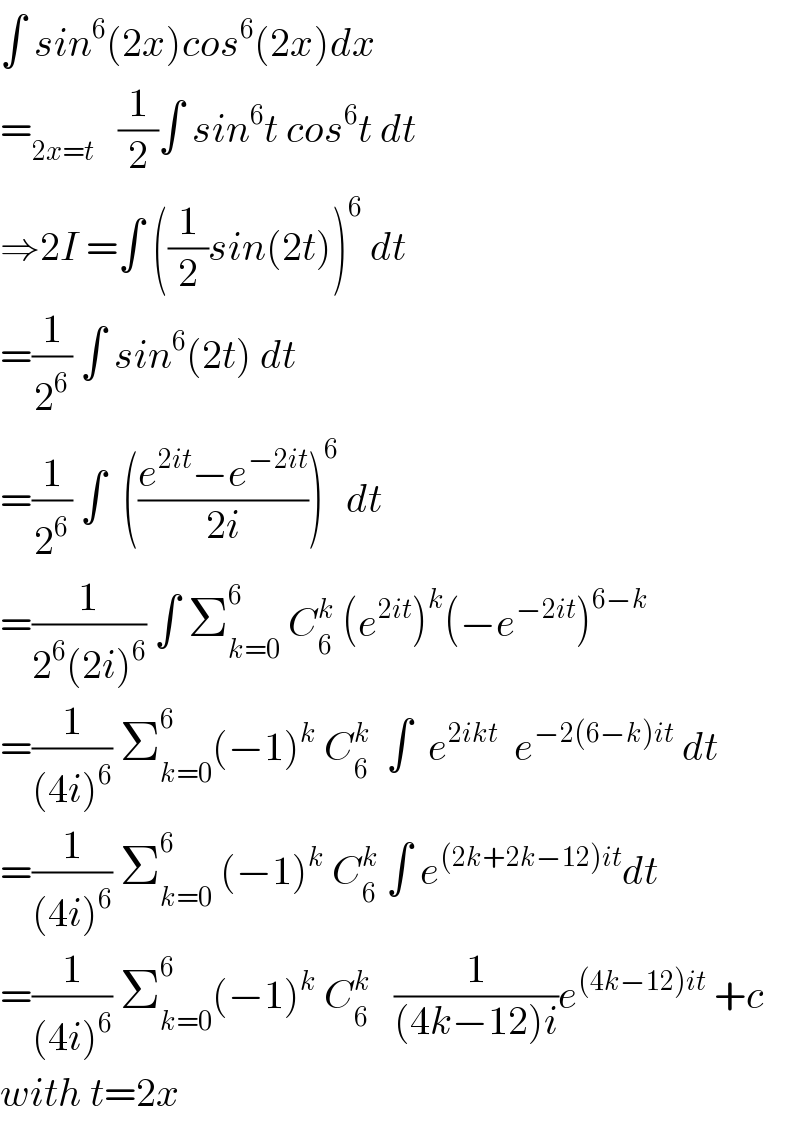
$$\int\:{sin}^{\mathrm{6}} \left(\mathrm{2}{x}\right){cos}^{\mathrm{6}} \left(\mathrm{2}{x}\right){dx} \\ $$$$=_{\mathrm{2}{x}={t}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}}\int\:{sin}^{\mathrm{6}} {t}\:{cos}^{\mathrm{6}} {t}\:{dt} \\ $$$$\Rightarrow\mathrm{2}{I}\:=\int\:\left(\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{t}\right)\right)^{\mathrm{6}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{6}} }\:\int\:{sin}^{\mathrm{6}} \left(\mathrm{2}{t}\right)\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{6}} }\:\int\:\:\left(\frac{{e}^{\mathrm{2}{it}} −{e}^{−\mathrm{2}{it}} }{\mathrm{2}{i}}\right)^{\mathrm{6}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{6}} \left(\mathrm{2}{i}\right)^{\mathrm{6}} }\:\int\:\sum_{{k}=\mathrm{0}} ^{\mathrm{6}} \:{C}_{\mathrm{6}} ^{{k}} \:\left({e}^{\mathrm{2}{it}} \right)^{{k}} \left(−{e}^{−\mathrm{2}{it}} \right)^{\mathrm{6}−{k}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{4}{i}\right)^{\mathrm{6}} }\:\sum_{{k}=\mathrm{0}} ^{\mathrm{6}} \left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{6}} ^{{k}} \:\:\int\:\:{e}^{\mathrm{2}{ikt}} \:\:{e}^{−\mathrm{2}\left(\mathrm{6}−{k}\right){it}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{4}{i}\right)^{\mathrm{6}} }\:\sum_{{k}=\mathrm{0}} ^{\mathrm{6}} \:\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{6}} ^{{k}} \:\int\:{e}^{\left(\mathrm{2}{k}+\mathrm{2}{k}−\mathrm{12}\right){it}} {dt} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{4}{i}\right)^{\mathrm{6}} }\:\sum_{{k}=\mathrm{0}} ^{\mathrm{6}} \left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{6}} ^{{k}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{4}{k}−\mathrm{12}\right){i}}{e}^{\left(\mathrm{4}{k}−\mathrm{12}\right){it}} \:+{c} \\ $$$${with}\:{t}=\mathrm{2}{x} \\ $$
