Menu Close

Can-we-prove-a-a-a-a-a-a-a-gt-1-

Tinku Tara 0 Comments
Pin




Question Number 5081 by FilupSmith last updated on 10/Apr/16
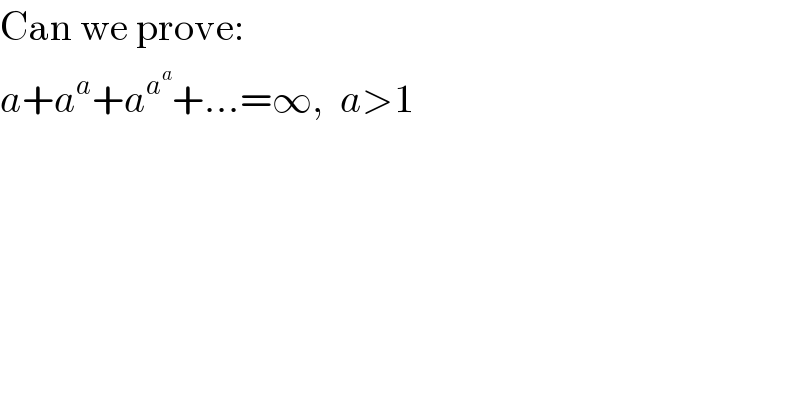
Can we prove: a+a^a +a^a^a +...=∞, a>1
$$\mathrm{Can}\:\mathrm{we}\:\mathrm{prove}: \\ $$$${a}+{a}^{{a}} +{a}^{{a}^{{a}} } +…=\infty,\:\:{a}>\mathrm{1} \\ $$
Answered by Yozzii last updated on 11/Apr/16
Define the function f that maps members of N+{0} to the n−th self−exponentiation of a>1, satisfying f(n+1)=a^(f(n)) ,f(0)=a. For example f(1)=a^(f(0)) =a^a and f(2)=a^(f(1)) =a^a^a . Further define the sum S of the first n outputs of f; i.e S(n)=Σ_(i=1) ^n f(i) or S(n)=a+a^a +a^a^a +...+a^(⋮^a (n−1 times self−exponentiation of a)) . Suppose for contradiction that lim_(n→∞) S(n) is finite. Then, ∃N∈N such that for all n>N, S(N+1)=S(N+2)=...=S(n)=... . Now, S(n) satisfies the recurrence equation S(n)−S(n−1)=f(n). Since a>1, then f(n)>0 for all n. ⇒S(n)−S(n−1)>0 or S(n)>S(n−1) for all n∈N. But, by the condition of convergence for sufficiently large n, S(n)=S(n−1). This is a contradiction that indicates lim_(n→∞) S(n) is nonfinite and in particular S(n)>S(n−1) so that S(n) is divergent. a+a^a +a^a^a +... is infinitely large in value.
$${Define}\:{the}\:{function}\:{f}\:{that}\:{maps}\: \\ $$$${members}\:{of}\:\mathbb{N}+\left\{\mathrm{0}\right\}\:{to}\:{the}\:\mathrm{n}−{th}\:{self}−{exponentiation} \\ $$$${of}\:{a}>\mathrm{1},\:{satisfying}\:{f}\left({n}+\mathrm{1}\right)={a}^{{f}\left({n}\right)} ,{f}\left(\mathrm{0}\right)={a}.\:{For}\:{example} \\ $$$${f}\left(\mathrm{1}\right)={a}^{{f}\left(\mathrm{0}\right)} ={a}^{{a}} \:{and}\:{f}\left(\mathrm{2}\right)={a}^{{f}\left(\mathrm{1}\right)} ={a}^{{a}^{{a}} } . \\ $$$${Further}\:{define}\:{the}\:{sum}\:{S}\:{of}\:{the}\:{first} \\ $$$${n}\:{outputs}\:{of}\:{f};\:{i}.{e}\:{S}\left({n}\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{f}\left({i}\right)\:{or} \\ $$$${S}\left({n}\right)={a}+{a}^{{a}} +{a}^{{a}^{{a}} } +…+{a}^{\vdots^{{a}} \:\:\:\left({n}−\mathrm{1}\:{times}\:{self}−{exponentiation}\:{of}\:{a}\right)} . \\ $$$${Suppose}\:{for}\:{contradiction}\:{that}\: \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{S}\left({n}\right)\:{is}\:{finite}.\:{Then},\:\exists{N}\in\mathbb{N}\:{such} \\ $$$${that}\:{for}\:{all}\:{n}>{N},\:{S}\left({N}+\mathrm{1}\right)={S}\left({N}+\mathrm{2}\right)=…={S}\left({n}\right)=…\:. \\ $$$${Now},\:{S}\left({n}\right)\:{satisfies}\:{the}\:{recurrence} \\ $$$${equation}\:{S}\left({n}\right)−{S}\left({n}−\mathrm{1}\right)={f}\left({n}\right). \\ $$$${Since}\:{a}>\mathrm{1},\:{then}\:{f}\left({n}\right)>\mathrm{0}\:{for}\:{all}\:{n}. \\ $$$$\Rightarrow{S}\left({n}\right)−{S}\left({n}−\mathrm{1}\right)>\mathrm{0}\:{or}\:{S}\left({n}\right)>{S}\left({n}−\mathrm{1}\right)\:{for}\:{all}\:{n}\in\mathbb{N}. \\ $$$${But},\:{by}\:{the}\:{condition}\:{of}\:{convergence} \\ $$$${for}\:{sufficiently}\:{large}\:{n},\:{S}\left({n}\right)={S}\left({n}−\mathrm{1}\right). \\ $$$${This}\:{is}\:{a}\:{contradiction}\:{that}\:{indicates} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{S}\left({n}\right)\:{is}\:{nonfinite}\:{and}\:{in}\:{particular} \\ $$$${S}\left({n}\right)>{S}\left({n}−\mathrm{1}\right)\:{so}\:{that}\:{S}\left({n}\right)\:{is}\:{divergent}. \\ $$$${a}+{a}^{{a}} +{a}^{{a}^{{a}} } +…\:{is}\:{infinitely}\:{large}\:{in} \\ $$$${value}.\: \\ $$$$ \\ $$$$ \\ $$
Commented by FilupSmith last updated on 11/Apr/16
Amazing proof!!
$${A}\mathrm{mazing}\:\mathrm{proof}!! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *