Question Number 182726 by SANOGO last updated on 13/Dec/22
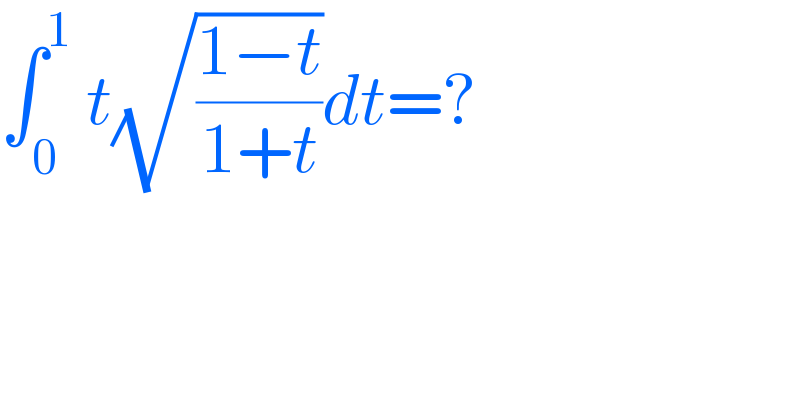
$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}\sqrt{\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}}{dt}=? \\ $$
Commented by CElcedricjunior last updated on 13/Dec/22
![∫_0 ^1 t(√((1−t)/(1+t)))dt=k posons (√((1−t)/(1+t)))=x ((1−t)/(1+t))=x^2 =>1−t=tx^2 +x^2 =>t=((1−x^2 )/(1+x^2 )) dt=((−4x)/((1+x^2 )^2 ))dx=>qd: { ((t=0)),((t=1)) :}=> { ((x=1)),((x=0)) :} k=∫_0 ^1 ((4x(1−x^2 ))/((1+x^2 )^3 ))dx=∫((−4x(x^2 +1)+8x)/((1+x^2 )^3 ))dx =∫_0 ^1 ((−4x)/((1+x^2 )^2 _ ))dx+∫_0 ^1 ((8x)/((1+x^2 )^3 ))dx =[(2/(1+x^2 ))]_0 ^1 −[(2/((1+x^2 )^2 ))]_0 ^1 =1−2−(1/2)+2 k=(1/2) ======================= ..........le celebre cedric junior........673804515 ====================================](https://www.tinkutara.com/question/Q182735.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{t}}\sqrt{\frac{\mathrm{1}−\boldsymbol{{t}}}{\mathrm{1}+\boldsymbol{{t}}}}\boldsymbol{{dt}}=\boldsymbol{{k}} \\ $$$$\boldsymbol{{posons}}\:\sqrt{\frac{\mathrm{1}−\boldsymbol{{t}}}{\mathrm{1}+\boldsymbol{{t}}}}=\boldsymbol{{x}} \\ $$$$\frac{\mathrm{1}−\boldsymbol{{t}}}{\mathrm{1}+\boldsymbol{{t}}}=\boldsymbol{{x}}^{\mathrm{2}} =>\mathrm{1}−\boldsymbol{{t}}=\boldsymbol{{tx}}^{\mathrm{2}} +\boldsymbol{{x}}^{\mathrm{2}} =>\boldsymbol{{t}}=\frac{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} } \\ $$$$\boldsymbol{{dt}}=\frac{−\mathrm{4}\boldsymbol{{x}}}{\left(\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} \right)^{\mathrm{2}} }\boldsymbol{{dx}}=>\boldsymbol{{qd}}:\begin{cases}{\boldsymbol{{t}}=\mathrm{0}}\\{\boldsymbol{{t}}=\mathrm{1}}\end{cases}=>\begin{cases}{\boldsymbol{{x}}=\mathrm{1}}\\{\boldsymbol{{x}}=\mathrm{0}}\end{cases} \\ $$$$\boldsymbol{{k}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{4}\boldsymbol{{x}}\left(\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} \right)^{\mathrm{3}} }\boldsymbol{{dx}}=\int\frac{−\mathrm{4}\boldsymbol{{x}}\left(\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{8}\boldsymbol{{x}}}{\left(\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} \right)^{\mathrm{3}} }\boldsymbol{{dx}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\mathrm{4}\boldsymbol{{x}}}{\left(\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} \underset{} {\right)}^{\mathrm{2}} }\boldsymbol{{dx}}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{8}\boldsymbol{{x}}}{\left(\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} \right)^{\mathrm{3}} }\boldsymbol{{dx}} \\ $$$$=\left[\frac{\mathrm{2}}{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} −\left[\frac{\mathrm{2}}{\left(\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} \right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{1}−\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2} \\ $$$$\boldsymbol{{k}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$======================= \\ $$$$……….{le}\:{celebre}\:{cedric}\:{junior}……..\mathrm{673804515} \\ $$$$==================================== \\ $$$$ \\ $$
Commented by ARUNG_Brandon_MBU last updated on 13/Dec/22
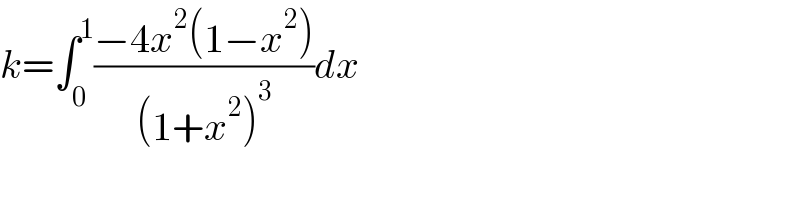
$${k}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }{dx} \\ $$
Commented by ARUNG_Brandon_MBU last updated on 13/Dec/22

Commented by SANOGO last updated on 13/Dec/22

$${merci} \\ $$
Answered by SEKRET last updated on 13/Dec/22

$$\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{t}}\centerdot\frac{\sqrt{\mathrm{1}−\boldsymbol{\mathrm{t}}^{\mathrm{2}} }}{\mathrm{1}+\boldsymbol{\mathrm{t}}}\:\boldsymbol{\mathrm{dt}}\:\:\:\begin{vmatrix}{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)=\:\boldsymbol{\mathrm{x}}}\\{\boldsymbol{\mathrm{dx}}=\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{t}}\right)\:\boldsymbol{\mathrm{dt}}}\end{vmatrix} \\ $$$$\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)\centerdot\frac{\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{t}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)}\centerdot\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{t}}\right)\:\boldsymbol{\mathrm{dt}}= \\ $$$$\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \frac{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)\centerdot\left(\mathrm{1}−\boldsymbol{\mathrm{sint}}\right)\left(\mathrm{1}+\boldsymbol{\mathrm{sint}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{sint}}}\boldsymbol{\mathrm{dt}}= \\ $$$$\int_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)\:−\:\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{t}}\right)\:\boldsymbol{\mathrm{dt}}= \\ $$$$\:\int_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)\boldsymbol{\mathrm{dt}}−\:\frac{\mathrm{1}}{\mathrm{2}}\centerdot\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \mathrm{1}−\boldsymbol{\mathrm{cos}}\left(\mathrm{2}\boldsymbol{\mathrm{t}}\right)\:\boldsymbol{\mathrm{dt}} \\ $$$$\:\:\:−\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{t}}\right)\:/_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{2}}\centerdot\boldsymbol{\mathrm{t}}+\frac{\mathrm{1}}{\mathrm{4}}\centerdot\boldsymbol{\mathrm{sin}}\left(\mathrm{2}\boldsymbol{\mathrm{t}}\right)\:/_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} = \\ $$$$\:\:\:\:−\left(\mathrm{0}−\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\boldsymbol{\pi}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\centerdot\mathrm{0}=\mathrm{1}−\frac{\boldsymbol{\pi}}{\mathrm{4}} \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \boldsymbol{\mathrm{t}}\centerdot\sqrt{\frac{\mathrm{1}−\boldsymbol{\mathrm{t}}}{\mathrm{1}+\boldsymbol{\mathrm{t}}}\:}\:\boldsymbol{\mathrm{dt}}\:\:=\:\:\mathrm{1}\:\:−\:\:\frac{\boldsymbol{\pi}}{\mathrm{4}} \\ $$$$\:\boldsymbol{{ABDULAZIZ}}\:\:\:\boldsymbol{{ABDUVALIYEV}} \\ $$
Answered by ARUNG_Brandon_MBU last updated on 13/Dec/22
![∫_0 ^1 t(√((1−t)/(1+t)))dt=∫_0 ^1 t∙((1−t)/( (√(1−t^2 ))))dt =∫_0 ^1 (t/( (√(1−t^2 ))))−∫_0 ^1 (t^2 /( (√(1−t^2 ))))dt =−[(√(1−t^2 ))]_0 ^1 −∫_0 ^(π/2) sin^2 θdθ =1−(1/2)∫_0 ^(π/2) (1−cos2θ)dθ=1−(π/4)](https://www.tinkutara.com/question/Q182730.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} {t}\sqrt{\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}}{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}\centerdot\frac{\mathrm{1}−{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt} \\ $$$$=−\left[\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{cos2}\theta\right){d}\theta=\mathrm{1}−\frac{\pi}{\mathrm{4}} \\ $$
