Menu Close

Question-182874

Tinku Tara 0 Comments
Pin




Question Number 182874 by peter frank last updated on 15/Dec/22
Answered by TheSupreme last updated on 16/Dec/22
V=vcos(θ)x^→ +(vsin(θ)−gt)y^→ S=vcos(θ)tx^→ +(vsin(θ)t−(1/2)gt^2 ) eq of plane y=tan(α)x if particle hits horizzontaly vsin(θ)−gt=0 t=((vsin(θ))/g) S^∗ =(v^2 /g)sin(θ)cos(θ)x^→ +(1/2)((v^2 sin^2 (θ))/g)y^→ y=tan(α)x (1/2)((v^2 sin^2 (θ))/g)=(v^2 /g)sin(θ)cos(θ)tan(α) (1/2)tan(θ)=tan(α) tan(θ)=2tan(α) d=(√(1+tan^2 (α)))x=(x/(cos(α)))=((v^2 sin(θ)cos(ϑ))/(gcos(α))) ... tan^2 (θ)=4tan^2 (α)→(1/(cos^2 (θ)))=1+4tan^2 (α) cos^2 (θ)=(1/(1+4tan^2 (α))) sin^2 (θ)=((4tan^2 (α))/(1+4tan^2 (α))) ... d=(v^2 /g)((2tan(α))/(1+4tan^2 (α)))(1/(cos(α)))
$${V}={vcos}\left(\theta\right)\overset{\rightarrow} {{x}}+\left({vsin}\left(\theta\right)−{gt}\right)\overset{\rightarrow} {{y}} \\ $$$${S}={vcos}\left(\theta\right){t}\overset{\rightarrow} {{x}}+\left({vsin}\left(\theta\right){t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \right) \\ $$$${eq}\:{of}\:{plane} \\ $$$${y}={tan}\left(\alpha\right){x} \\ $$$$ \\ $$$${if}\:{particle}\:{hits}\:{horizzontaly} \\ $$$${vsin}\left(\theta\right)−{gt}=\mathrm{0} \\ $$$${t}=\frac{{vsin}\left(\theta\right)}{{g}} \\ $$$${S}^{\ast} =\frac{{v}^{\mathrm{2}} }{{g}}{sin}\left(\theta\right){cos}\left(\theta\right)\overset{\rightarrow} {{x}}+\frac{\mathrm{1}}{\mathrm{2}}\frac{{v}^{\mathrm{2}} {sin}^{\mathrm{2}} \left(\theta\right)}{{g}}\overset{\rightarrow} {{y}} \\ $$$${y}={tan}\left(\alpha\right){x} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\frac{{v}^{\mathrm{2}} {sin}^{\mathrm{2}} \left(\theta\right)}{{g}}=\frac{{v}^{\mathrm{2}} }{{g}}{sin}\left(\theta\right){cos}\left(\theta\right){tan}\left(\alpha\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{tan}\left(\theta\right)={tan}\left(\alpha\right) \\ $$$${tan}\left(\theta\right)=\mathrm{2}{tan}\left(\alpha\right) \\ $$$${d}=\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \left(\alpha\right)}{x}=\frac{{x}}{{cos}\left(\alpha\right)}=\frac{{v}^{\mathrm{2}} {sin}\left(\theta\right){cos}\left(\vartheta\right)}{{gcos}\left(\alpha\right)} \\ $$$$… \\ $$$${tan}^{\mathrm{2}} \left(\theta\right)=\mathrm{4}{tan}^{\mathrm{2}} \left(\alpha\right)\rightarrow\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left(\theta\right)}=\mathrm{1}+\mathrm{4}{tan}^{\mathrm{2}} \left(\alpha\right) \\ $$$${cos}^{\mathrm{2}} \left(\theta\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{4}{tan}^{\mathrm{2}} \left(\alpha\right)} \\ $$$${sin}^{\mathrm{2}} \left(\theta\right)=\frac{\mathrm{4}{tan}^{\mathrm{2}} \left(\alpha\right)}{\mathrm{1}+\mathrm{4}{tan}^{\mathrm{2}} \left(\alpha\right)} \\ $$$$… \\ $$$${d}=\frac{{v}^{\mathrm{2}} }{{g}}\frac{\mathrm{2}{tan}\left(\alpha\right)}{\mathrm{1}+\mathrm{4}{tan}^{\mathrm{2}} \left(\alpha\right)}\frac{\mathrm{1}}{{cos}\left(\alpha\right)} \\ $$
Commented by peter frank last updated on 17/Dec/22
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by peter frank last updated on 31/Dec/22
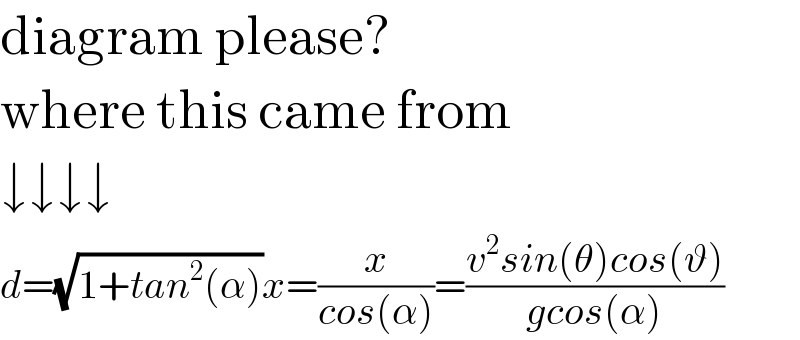
diagram please? where this came from ↓↓↓↓ d=(√(1+tan^2 (α)))x=(x/(cos(α)))=((v^2 sin(θ)cos(ϑ))/(gcos(α)))
$$\mathrm{diagram}\:\mathrm{please}? \\ $$$$\mathrm{where}\:\mathrm{this}\:\mathrm{came}\:\mathrm{from} \\ $$$$\downarrow\downarrow\downarrow\downarrow \\ $$$${d}=\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \left(\alpha\right)}{x}=\frac{{x}}{{cos}\left(\alpha\right)}=\frac{{v}^{\mathrm{2}} {sin}\left(\theta\right){cos}\left(\vartheta\right)}{{gcos}\left(\alpha\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *