Question Number 182900 by greougoury555 last updated on 16/Dec/22
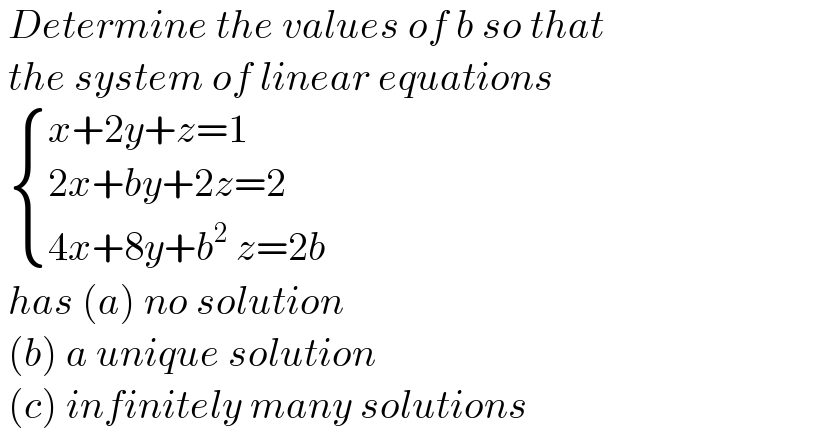
$$\:{Determine}\:{the}\:{values}\:{of}\:{b}\:{so}\:{that} \\ $$$$\:{the}\:{system}\:{of}\:{linear}\:{equations} \\ $$$$\:\begin{cases}{{x}+\mathrm{2}{y}+{z}=\mathrm{1}}\\{\mathrm{2}{x}+{by}+\mathrm{2}{z}=\mathrm{2}}\\{\mathrm{4}{x}+\mathrm{8}{y}+{b}^{\mathrm{2}} \:{z}=\mathrm{2}{b}}\end{cases} \\ $$$$\:{has}\:\left({a}\right)\:{no}\:{solution}\: \\ $$$$\:\left({b}\right)\:{a}\:{unique}\:{solution} \\ $$$$\:\left({c}\right)\:{infinitely}\:{many}\:{solutions} \\ $$
Answered by cortano1 last updated on 16/Dec/22
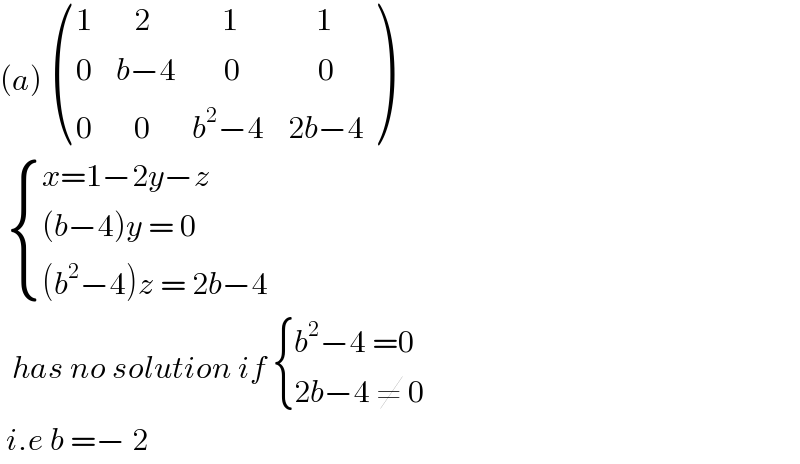
$$\left({a}\right)\:\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{0}\:\:\:\:{b}−\mathrm{4}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:{b}^{\mathrm{2}} −\mathrm{4}\:\:\:\:\mathrm{2}{b}−\mathrm{4}}\end{pmatrix} \\ $$$$\:\begin{cases}{{x}=\mathrm{1}−\mathrm{2}{y}−{z}}\\{\left({b}−\mathrm{4}\right){y}\:=\:\mathrm{0}}\\{\left({b}^{\mathrm{2}} −\mathrm{4}\right){z}\:=\:\mathrm{2}{b}−\mathrm{4}}\end{cases} \\ $$$$\:\:{has}\:{no}\:{solution}\:{if}\:\begin{cases}{{b}^{\mathrm{2}} −\mathrm{4}\:=\mathrm{0}}\\{\mathrm{2}{b}−\mathrm{4}\:\neq\:\mathrm{0}}\end{cases} \\ $$$$\:{i}.{e}\:{b}\:=−\:\mathrm{2} \\ $$
Commented by manolex last updated on 16/Dec/22
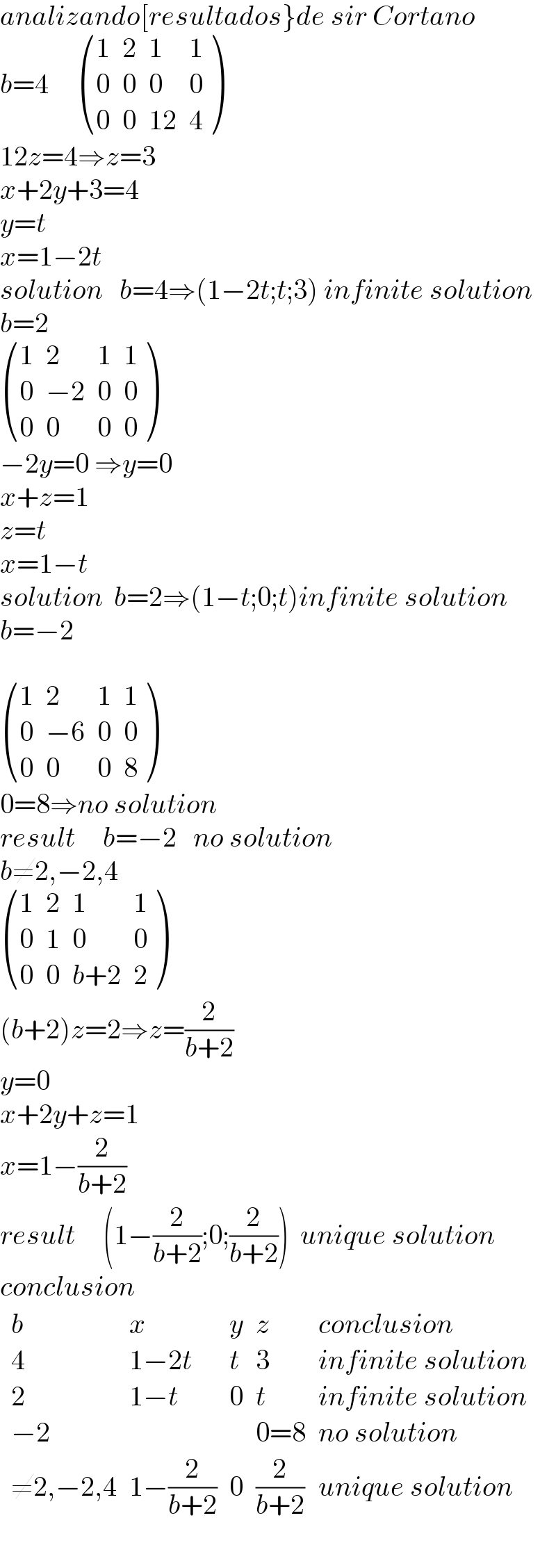
$${analizando}\left[{resultados}\right\}{de}\:{sir}\:{Cortano} \\ $$$${b}=\mathrm{4}\:\:\:\:\:\begin{pmatrix}{\mathrm{1}}&{\mathrm{2}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{0}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{12}}&{\mathrm{4}}\end{pmatrix} \\ $$$$\mathrm{12}{z}=\mathrm{4}\Rightarrow{z}=\mathrm{3} \\ $$$${x}+\mathrm{2}{y}+\mathrm{3}=\mathrm{4} \\ $$$${y}={t} \\ $$$${x}=\mathrm{1}−\mathrm{2}{t} \\ $$$${solution}\:\:\:{b}=\mathrm{4}\Rightarrow\left(\mathrm{1}−\mathrm{2}{t};{t};\mathrm{3}\right)\:{infinite}\:{solution} \\ $$$${b}=\mathrm{2} \\ $$$$\begin{pmatrix}{\mathrm{1}}&{\mathrm{2}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{0}}&{−\mathrm{2}}&{\mathrm{0}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{0}}&{\mathrm{0}}\end{pmatrix} \\ $$$$−\mathrm{2}{y}=\mathrm{0}\:\Rightarrow{y}=\mathrm{0} \\ $$$${x}+{z}=\mathrm{1} \\ $$$${z}={t} \\ $$$${x}=\mathrm{1}−{t} \\ $$$${solution}\:\:{b}=\mathrm{2}\Rightarrow\left(\mathrm{1}−{t};\mathrm{0};{t}\right){infinite}\:{solution} \\ $$$${b}=−\mathrm{2} \\ $$$$ \\ $$$$\begin{pmatrix}{\mathrm{1}}&{\mathrm{2}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{0}}&{−\mathrm{6}}&{\mathrm{0}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{0}}&{\mathrm{8}}\end{pmatrix} \\ $$$$\mathrm{0}=\mathrm{8}\Rightarrow{no}\:{solution} \\ $$$${result}\:\:\:\:\:{b}=−\mathrm{2}\:\:\:{no}\:{solution} \\ $$$${b}\neq\mathrm{2},−\mathrm{2},\mathrm{4} \\ $$$$\begin{pmatrix}{\mathrm{1}}&{\mathrm{2}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{1}}&{\mathrm{0}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{0}}&{{b}+\mathrm{2}}&{\mathrm{2}}\end{pmatrix} \\ $$$$\left({b}+\mathrm{2}\right){z}=\mathrm{2}\Rightarrow{z}=\frac{\mathrm{2}}{{b}+\mathrm{2}} \\ $$$${y}=\mathrm{0} \\ $$$${x}+\mathrm{2}{y}+{z}=\mathrm{1} \\ $$$${x}=\mathrm{1}−\frac{\mathrm{2}}{{b}+\mathrm{2}} \\ $$$${result}\:\:\:\:\:\left(\mathrm{1}−\frac{\mathrm{2}}{{b}+\mathrm{2}};\mathrm{0};\frac{\mathrm{2}}{{b}+\mathrm{2}}\right)\:\:{unique}\:{solution} \\ $$$${conclusion} \\ $$$$\begin{array}{|c|c|c|c|c|}{{b}}&\hline{{x}}&\hline{{y}}&\hline{{z}}&\hline{{conclusion}}\\{\mathrm{4}}&\hline{\mathrm{1}−\mathrm{2}{t}}&\hline{{t}}&\hline{\mathrm{3}}&\hline{{infinite}\:{solution}}\\{\mathrm{2}}&\hline{\mathrm{1}−{t}}&\hline{\mathrm{0}}&\hline{{t}}&\hline{{infinite}\:{solution}}\\{−\mathrm{2}}&\hline{}&\hline{}&\hline{\mathrm{0}=\mathrm{8}}&\hline{{no}\:{solution}}\\{\neq\mathrm{2},−\mathrm{2},\mathrm{4}}&\hline{\mathrm{1}−\frac{\mathrm{2}}{{b}+\mathrm{2}}}&\hline{\mathrm{0}}&\hline{\frac{\mathrm{2}}{{b}+\mathrm{2}}}&\hline{{unique}\:{solution}}\\\hline\end{array} \\ $$$$ \\ $$
