Menu Close

lim-x-0-1-tan-2-x-1-2x-

Tinku Tara 0 Comments
Pin




Question Number 117545 by Lordose last updated on 12/Oct/20
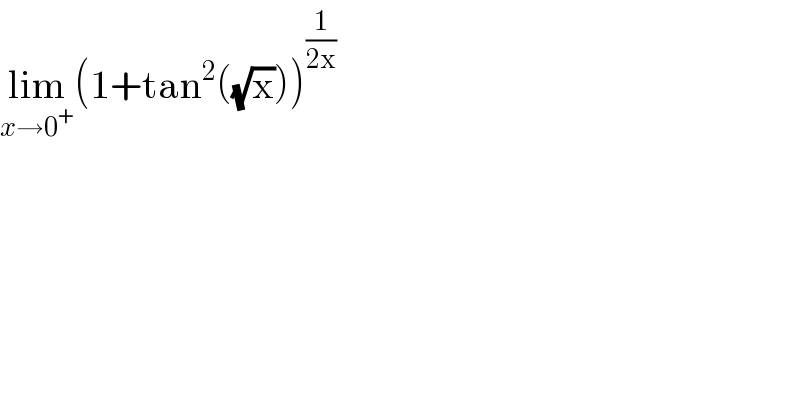
lim_(x→0^+ ) (1+tan^2 ((√x)))^(1/(2x))
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\sqrt{\mathrm{x}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{2x}}} \\ $$
Answered by TANMAY PANACEA last updated on 12/Oct/20
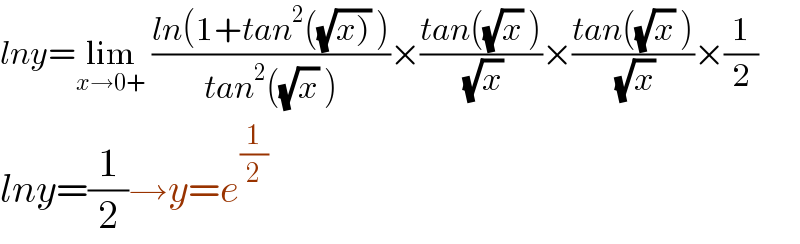
lny=lim_(x→0+) ((ln(1+tan^2 ((√(x))) ))/(tan^2 ((√x) )))×((tan((√x) ))/( (√x)))×((tan((√x) ))/( (√x)))×(1/2) lny=(1/2)→y=e^(1/2)
$${lny}=\underset{{x}\rightarrow\mathrm{0}+} {\mathrm{lim}}\:\frac{{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\sqrt{\left.{x}\right)}\:\right)\right.}{{tan}^{\mathrm{2}} \left(\sqrt{{x}}\:\right)}×\frac{{tan}\left(\sqrt{{x}}\:\right)}{\:\sqrt{{x}}}×\frac{{tan}\left(\sqrt{{x}}\:\right)}{\:\sqrt{{x}}}×\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${lny}=\frac{\mathrm{1}}{\mathrm{2}}\rightarrow{y}={e}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$
Answered by Olaf last updated on 12/Oct/20
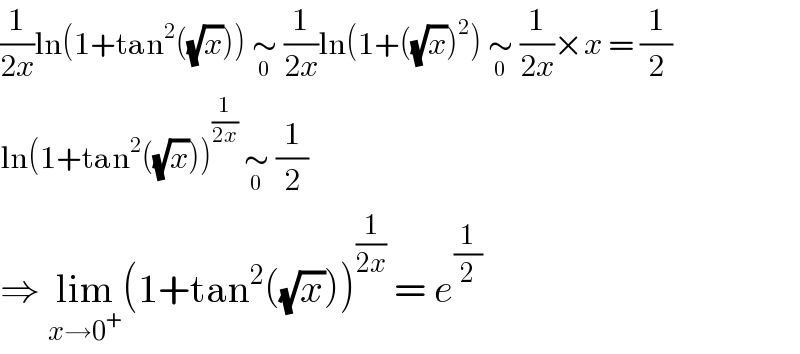
(1/(2x))ln(1+tan^2 ((√x))) ∼_0 (1/(2x))ln(1+((√x))^2 ) ∼_0 (1/(2x))×x = (1/2) ln(1+tan^2 ((√x)))^(1/(2x)) ∼_0 (1/2) ⇒ lim_(x→0^+ ) (1+tan^2 ((√x)))^(1/(2x)) = e^(1/2)
$$\frac{\mathrm{1}}{\mathrm{2}{x}}\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\sqrt{{x}}\right)\right)\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{1}}{\mathrm{2}{x}}\mathrm{ln}\left(\mathrm{1}+\left(\sqrt{{x}}\right)^{\mathrm{2}} \right)\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{1}}{\mathrm{2}{x}}×{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\sqrt{{x}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{2}{x}}} \:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\sqrt{{x}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{2}{x}}} \:=\:{e}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$
Answered by Dwaipayan Shikari last updated on 12/Oct/20
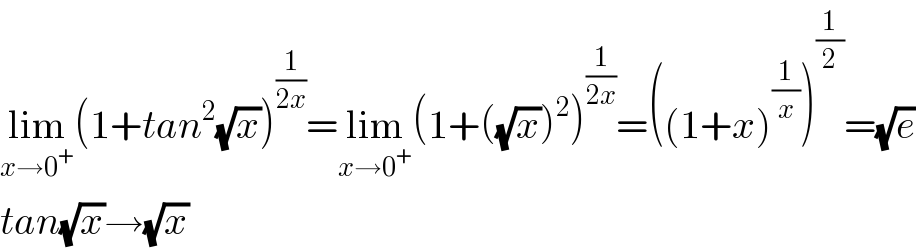
lim_(x→0^+ ) (1+tan^2 (√x))^(1/(2x)) =lim_(x→0^+ ) (1+((√x))^2 )^(1/(2x)) =((1+x)^(1/x) )^(1/2) =(√e) tan(√x)→(√x)
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\mathrm{1}+{tan}^{\mathrm{2}} \sqrt{{x}}\right)^{\frac{\mathrm{1}}{\mathrm{2}{x}}} =\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\mathrm{1}+\left(\sqrt{{x}}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}{x}}} =\left(\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\sqrt{{e}} \\ $$$${tan}\sqrt{{x}}\rightarrow\sqrt{{x}} \\ $$
Answered by bobhans last updated on 12/Oct/20
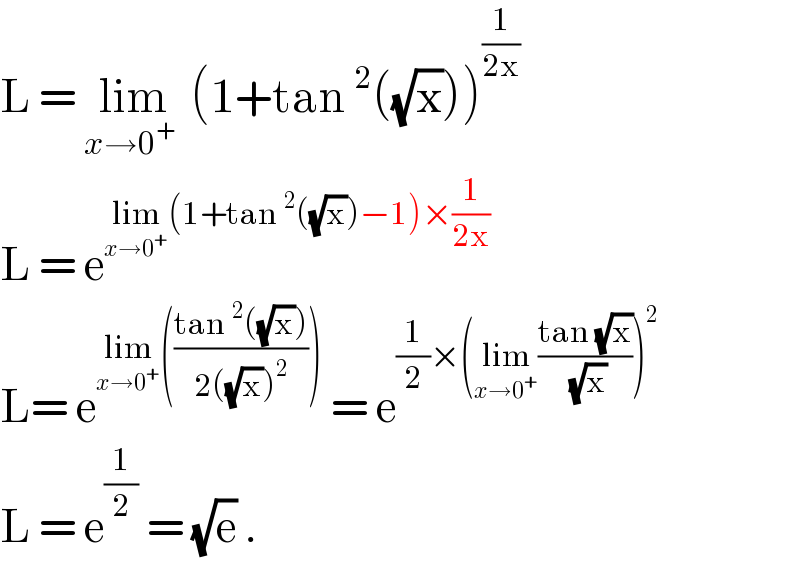
L = lim_(x→0^+ ) (1+tan^2 ((√x)))^(1/(2x)) L = e^(lim_(x→0^+ ) (1+tan^2 ((√x))−1)×(1/(2x))) L= e^(lim_(x→0^+ ) (((tan^2 ((√x)))/(2((√x))^2 )))) = e^((1/2)×(lim_(x→0^+ ) ((tan (√x))/( (√x))))^2 ) L = e^(1/2) = (√e) .
$$\mathrm{L}\:=\:\underset{{x}\rightarrow\mathrm{0}^{+} \:} {\mathrm{lim}}\:\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\sqrt{\mathrm{x}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{2x}}} \\ $$$$\mathrm{L}\:=\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\sqrt{\mathrm{x}}\right)−\mathrm{1}\right)×\frac{\mathrm{1}}{\mathrm{2x}}} \\ $$$$\mathrm{L}=\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\frac{\mathrm{tan}\:^{\mathrm{2}} \left(\sqrt{\mathrm{x}}\right)}{\mathrm{2}\left(\sqrt{\mathrm{x}}\right)^{\mathrm{2}} }\right)} \:=\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}×\left(\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{tan}\:\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{x}}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{L}\:=\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\sqrt{\mathrm{e}}\:.\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *