Question Number 70659 by aliesam last updated on 06/Oct/19
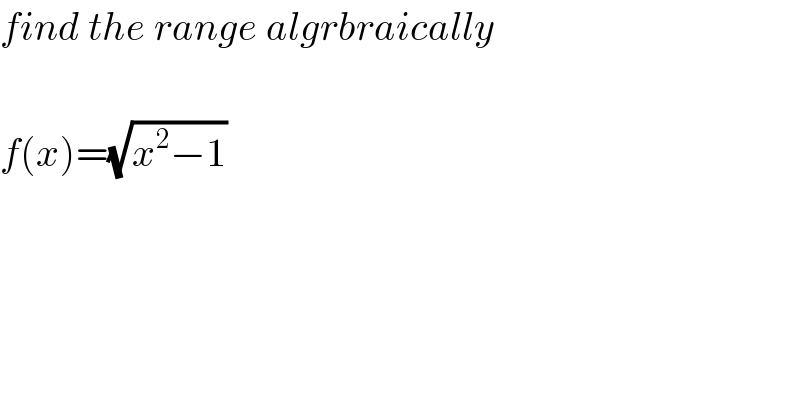
$${find}\:{the}\:{range}\:{algrbraically} \\ $$$$ \\ $$$${f}\left({x}\right)=\sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$
Answered by MJS last updated on 06/Oct/19
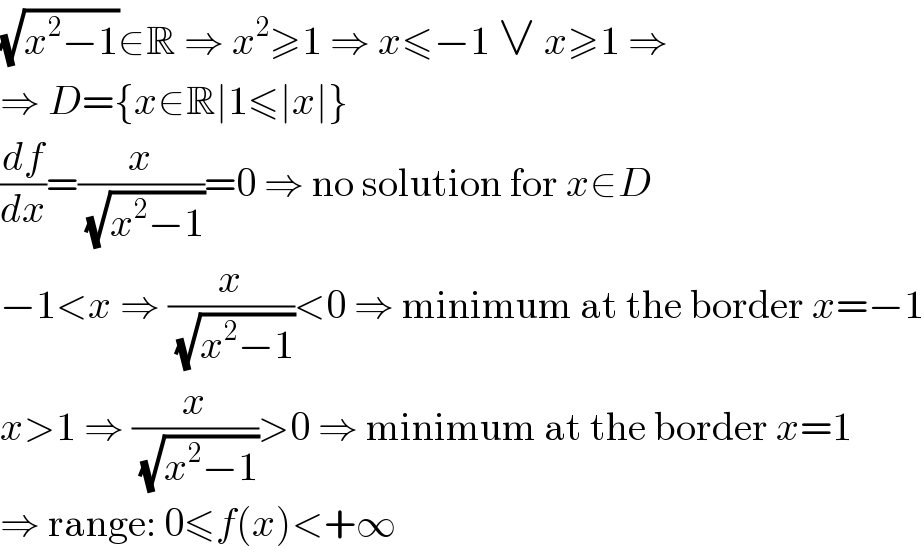
$$\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\in\mathbb{R}\:\Rightarrow\:{x}^{\mathrm{2}} \geqslant\mathrm{1}\:\Rightarrow\:{x}\leqslant−\mathrm{1}\:\vee\:{x}\geqslant\mathrm{1}\:\Rightarrow \\ $$$$\Rightarrow\:{D}=\left\{{x}\in\mathbb{R}\mid\mathrm{1}\leqslant\mid{x}\mid\right\} \\ $$$$\frac{{df}}{{dx}}=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}=\mathrm{0}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution}\:\mathrm{for}\:{x}\in{D} \\ $$$$−\mathrm{1}<{x}\:\Rightarrow\:\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}<\mathrm{0}\:\Rightarrow\:\mathrm{minimum}\:\mathrm{at}\:\mathrm{the}\:\mathrm{border}\:{x}=−\mathrm{1} \\ $$$${x}>\mathrm{1}\:\Rightarrow\:\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}>\mathrm{0}\:\Rightarrow\:\mathrm{minimum}\:\mathrm{at}\:\mathrm{the}\:\mathrm{border}\:{x}=\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{range}:\:\mathrm{0}\leqslant{f}\left({x}\right)<+\infty \\ $$
