lim-x-0-sinx-x-x-3-

Question Number 183136 by mathlove last updated on 21/Dec/22

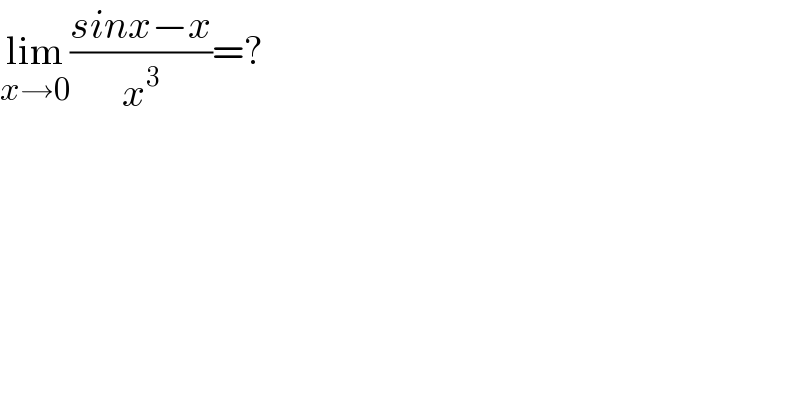
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sinx}−{x}}{{x}^{\mathrm{3}} }=? \\ $$

Answered by TheSupreme last updated on 21/Dec/22

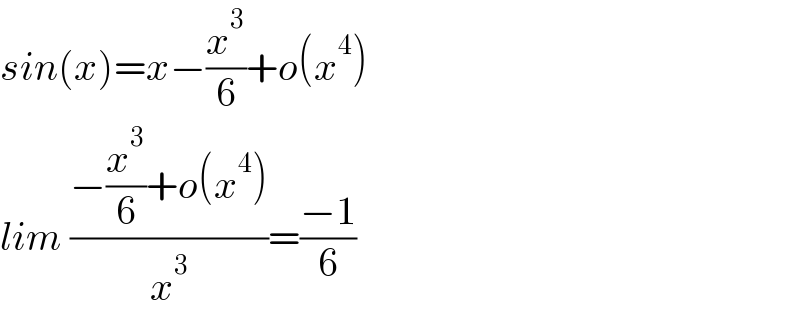
sin(x)=x−(x^3 /6)+o(x^4 ) lim ((−(x^3 /6)+o(x^4 ))/x^3 )=((−1)/6)

$${sin}\left({x}\right)={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{o}\left({x}^{\mathrm{4}} \right) \\ $$$${lim}\:\frac{−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{o}\left({x}^{\mathrm{4}} \right)}{{x}^{\mathrm{3}} }=\frac{−\mathrm{1}}{\mathrm{6}} \\ $$

Answered by CrispyXYZ last updated on 21/Dec/22

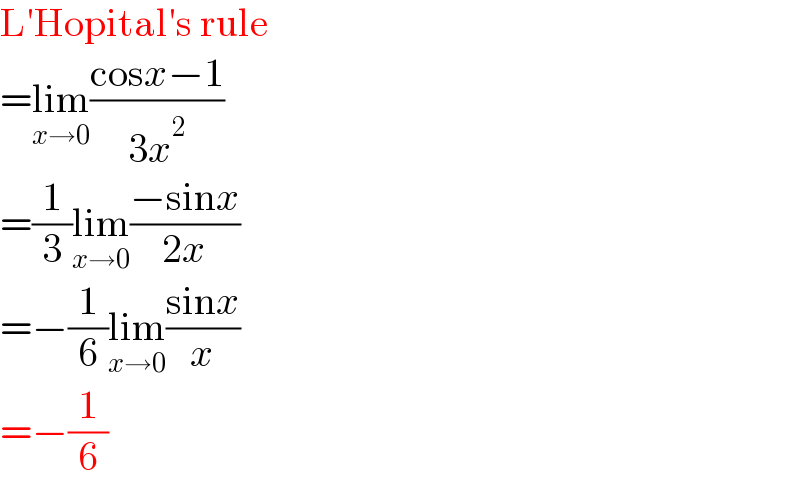
L′Hopital′s rule =lim_(x→0) ((cosx−1)/(3x^2 )) =(1/3)lim_(x→0) ((−sinx)/(2x)) =−(1/6)lim_(x→0) ((sinx)/x) =−(1/6)

$$\mathrm{L}'\mathrm{Hopital}'\mathrm{s}\:\mathrm{rule} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}{x}−\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{sin}{x}}{\mathrm{2}{x}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}{x}}{{x}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Commented by TheSupreme last updated on 21/Dec/22

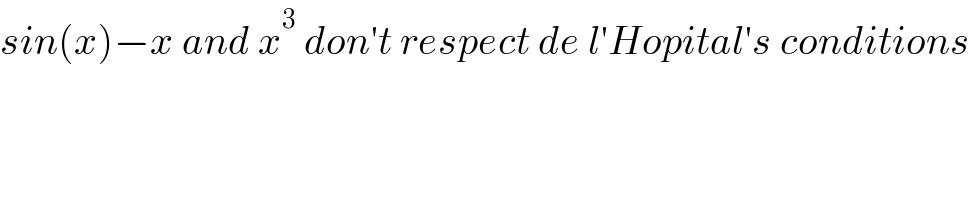
sin(x)−x and x^3 don′t respect de l′Hopital′s conditions

$${sin}\left({x}\right)−{x}\:{and}\:{x}^{\mathrm{3}} \:{don}'{t}\:{respect}\:{de}\:{l}'{Hopital}'{s}\:{conditions} \\ $$

Commented by MJS_new last updated on 21/Dec/22

why not? with x=0 we have sin x −x=0 ∧ x^3 =0 (((d^3 [sin x −x])/dx^3 )/((d^3 [x^3 ])/dx^3 ))=((−cos x)/6)=_(x=0) −(1/6)

$$\mathrm{why}\:\mathrm{not}?\:\mathrm{with}\:{x}=\mathrm{0}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{sin}\:{x}\:−{x}=\mathrm{0}\:\wedge\:{x}^{\mathrm{3}} =\mathrm{0} \\ $$$$\frac{\frac{{d}^{\mathrm{3}} \left[\mathrm{sin}\:{x}\:−{x}\right]}{{dx}^{\mathrm{3}} }}{\frac{{d}^{\mathrm{3}} \left[{x}^{\mathrm{3}} \right]}{{dx}^{\mathrm{3}} }}=\frac{−\mathrm{cos}\:{x}}{\mathrm{6}}\underset{{x}=\mathrm{0}} {=}−\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Answered by CrispyXYZ last updated on 21/Dec/22

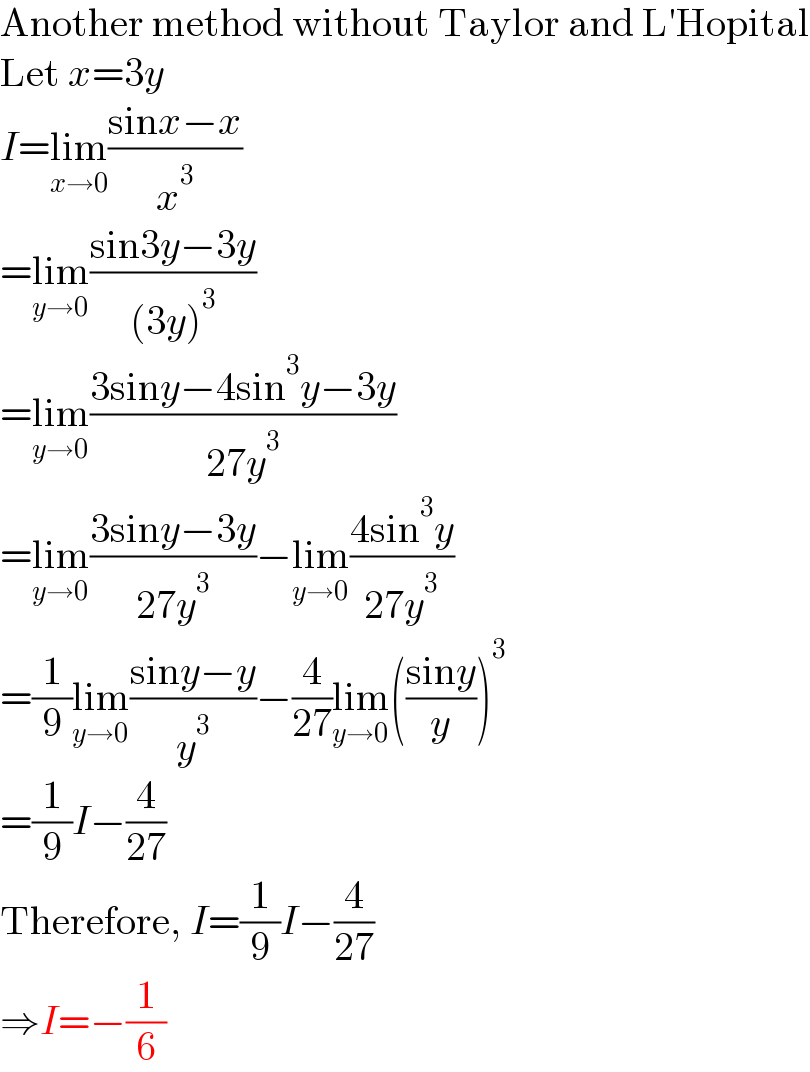
Another method without Taylor and L′Hopital Let x=3y I=lim_(x→0) ((sinx−x)/x^3 ) =lim_(y→0) ((sin3y−3y)/((3y)^3 )) =lim_(y→0) ((3siny−4sin^3 y−3y)/(27y^3 )) =lim_(y→0) ((3siny−3y)/(27y^3 ))−lim_(y→0) ((4sin^3 y)/(27y^3 )) =(1/9)lim_(y→0) ((siny−y)/y^3 )−(4/(27))lim_(y→0) (((siny)/y))^3 =(1/9)I−(4/(27)) Therefore, I=(1/9)I−(4/(27)) ⇒I=−(1/6)

$$\mathrm{Another}\:\mathrm{method}\:\mathrm{without}\:\mathrm{Taylor}\:\mathrm{and}\:\mathrm{L}'\mathrm{Hopital} \\ $$$$\mathrm{Let}\:{x}=\mathrm{3}{y} \\ $$$${I}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}{x}−{x}}{{x}^{\mathrm{3}} } \\ $$$$=\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin3}{y}−\mathrm{3}{y}}{\left(\mathrm{3}{y}\right)^{\mathrm{3}} } \\ $$$$=\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3sin}{y}−\mathrm{4sin}^{\mathrm{3}} {y}−\mathrm{3}{y}}{\mathrm{27}{y}^{\mathrm{3}} } \\ $$$$=\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3sin}{y}−\mathrm{3}{y}}{\mathrm{27}{y}^{\mathrm{3}} }−\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{4sin}^{\mathrm{3}} {y}}{\mathrm{27}{y}^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}{y}−{y}}{{y}^{\mathrm{3}} }−\frac{\mathrm{4}}{\mathrm{27}}\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}{y}}{{y}}\right)^{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}{I}−\frac{\mathrm{4}}{\mathrm{27}} \\ $$$$\mathrm{Therefore},\:{I}=\frac{\mathrm{1}}{\mathrm{9}}{I}−\frac{\mathrm{4}}{\mathrm{27}} \\ $$$$\Rightarrow{I}=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Commented by MJS_new last updated on 21/Dec/22

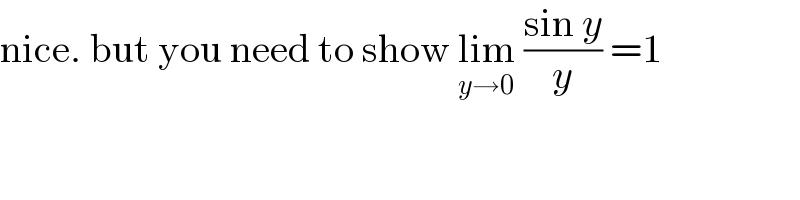
nice. but you need to show lim_(y→0) ((sin y)/y) =1

$$\mathrm{nice}.\:\mathrm{but}\:\mathrm{you}\:\mathrm{need}\:\mathrm{to}\:\mathrm{show}\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{y}}{{y}}\:=\mathrm{1} \\ $$

Commented by CrispyXYZ last updated on 21/Dec/22

We can simply use equivalent infinitesimal: sinx ∼ x So lim_(x→0) ((sinx)/x)=1 Another way is to draw a circle x^2 +y^2 =1 construct an angle θ(rad) so one of the intersect is (cosθ, sinθ). length of the arc is θ it is easy to show that lim_(θ→0) ((sinθ)/θ)=1

$$\mathrm{We}\:\mathrm{can}\:\mathrm{simply}\:\mathrm{use}\:\mathrm{equivalent}\:\mathrm{infinitesimal}: \\ $$$$\mathrm{sin}{x}\:\sim\:{x} \\ $$$$\mathrm{So}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}{x}}{{x}}=\mathrm{1} \\ $$$$\mathrm{Another}\:\mathrm{way}\:\mathrm{is}\:\mathrm{to}\:\mathrm{draw}\:\mathrm{a}\:\mathrm{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{construct}\:\mathrm{an}\:\mathrm{angle}\:\theta\left(\mathrm{rad}\right)\:\mathrm{so}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{intersect}\:\mathrm{is} \\ $$$$\left(\mathrm{cos}\theta,\:\mathrm{sin}\theta\right).\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{arc}\:\mathrm{is}\:\theta \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that} \\ $$$$\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\theta}{\theta}=\mathrm{1} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply