Menu Close

Let-P-x-be-a-polynomial-function-of-degree-n-such-that-P-k-k-k-1-for-k-0-1-2-n-Then-P-n-1-is-equal-to-A-1-if-n-is-even-B-1-if-n-is-odd-C-n-n-2-if-n-is-even-

Tinku Tara 0 Comments
Pin




Question Number 117649 by Ar Brandon last updated on 13/Oct/20
Let P(x) be a polynomial function of degree n such that P(k)=(k/(k+1)) for k=0,1,2,...,n. Then P(n+1) is equal to (A) −1 if n is even (B) 1 if n is odd (C) (n/(n+2)) if n is even (D) (n/(n+2)) if n is odd Which among the four proposals is/are correct ?
$$\mathrm{Let}\:\mathrm{P}\left({x}\right)\:\mathrm{be}\:\mathrm{a}\:\mathrm{polynomial}\:\mathrm{function}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{n}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{P}\left({k}\right)=\frac{{k}}{{k}+\mathrm{1}}\:\:\mathrm{for}\:{k}=\mathrm{0},\mathrm{1},\mathrm{2},…,\mathrm{n}.\:\mathrm{Then}\:\mathrm{P}\left(\mathrm{n}+\mathrm{1}\right)\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\: \\ $$$$\left(\mathrm{A}\right)\:−\mathrm{1}\:\mathrm{if}\:\mathrm{n}\:\mathrm{is}\:\mathrm{even}\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{B}\right)\:\mathrm{1}\:\mathrm{if}\:{n}\:\mathrm{is}\:\mathrm{odd} \\ $$$$\left(\mathrm{C}\right)\:\frac{{n}}{{n}+\mathrm{2}}\:\mathrm{if}\:{n}\:\mathrm{is}\:\mathrm{even}\:\:\:\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:\frac{{n}}{{n}+\mathrm{2}}\:\:\mathrm{if}\:{n}\:\mathrm{is}\:\mathrm{odd} \\ $$$$\mathrm{Which}\:\mathrm{among}\:\mathrm{the}\:\mathrm{four}\:\mathrm{proposals}\:\mathrm{is}/\mathrm{are}\:\mathrm{correct}\:? \\ $$
Answered by prakash jain last updated on 13/Oct/20
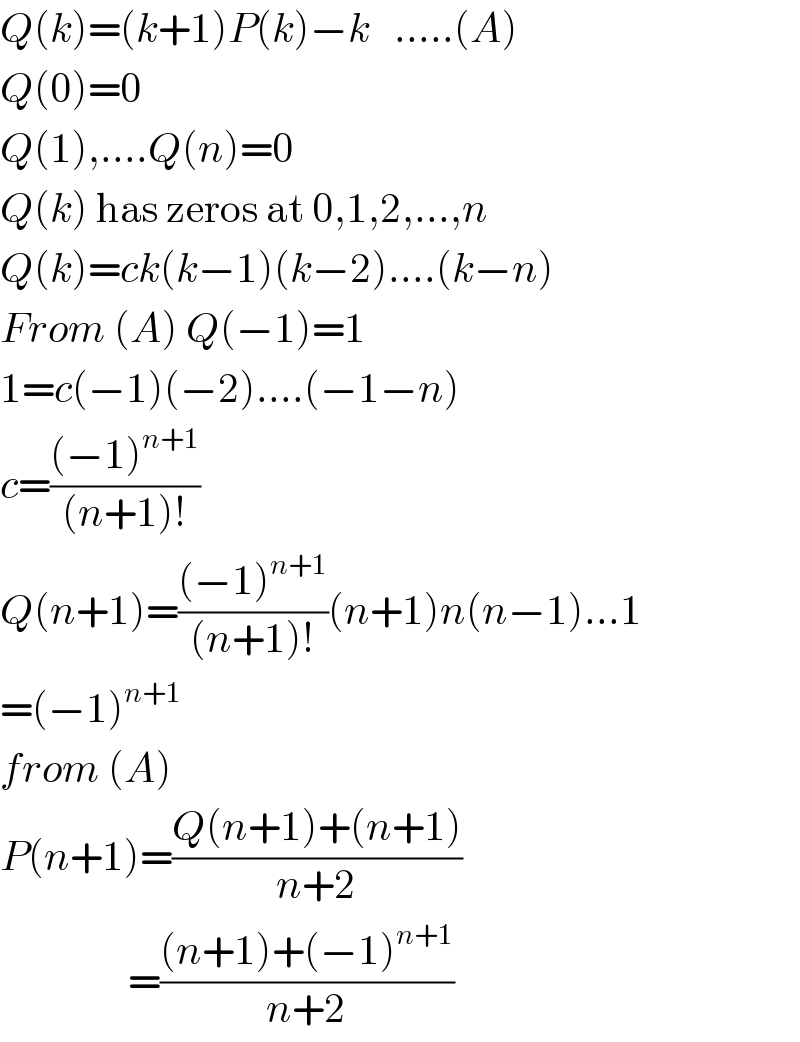
Q(k)=(k+1)P(k)−k .....(A) Q(0)=0 Q(1),....Q(n)=0 Q(k) has zeros at 0,1,2,...,n Q(k)=ck(k−1)(k−2)....(k−n) From (A) Q(−1)=1 1=c(−1)(−2)....(−1−n) c=(((−1)^(n+1) )/((n+1)!)) Q(n+1)=(((−1)^(n+1) )/((n+1)!))(n+1)n(n−1)...1 =(−1)^(n+1) from (A) P(n+1)=((Q(n+1)+(n+1))/(n+2)) =(((n+1)+(−1)^(n+1) )/(n+2))
$${Q}\left({k}\right)=\left({k}+\mathrm{1}\right){P}\left({k}\right)−{k}\:\:\:…..\left({A}\right) \\ $$$${Q}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${Q}\left(\mathrm{1}\right),….{Q}\left({n}\right)=\mathrm{0} \\ $$$${Q}\left({k}\right)\:\mathrm{has}\:\mathrm{zeros}\:\mathrm{at}\:\mathrm{0},\mathrm{1},\mathrm{2},…,{n} \\ $$$${Q}\left({k}\right)={ck}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)….\left({k}−{n}\right) \\ $$$${From}\:\left({A}\right)\:{Q}\left(−\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{1}={c}\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)….\left(−\mathrm{1}−{n}\right) \\ $$$${c}=\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)!} \\ $$$${Q}\left({n}+\mathrm{1}\right)=\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)!}\left({n}+\mathrm{1}\right){n}\left({n}−\mathrm{1}\right)…\mathrm{1} \\ $$$$=\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \\ $$$${from}\:\left({A}\right) \\ $$$${P}\left({n}+\mathrm{1}\right)=\frac{{Q}\left({n}+\mathrm{1}\right)+\left({n}+\mathrm{1}\right)}{{n}+\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({n}+\mathrm{1}\right)+\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{2}} \\ $$
Commented by Ar Brandon last updated on 13/Oct/20
Thank You Sir

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *