Question Number 52223 by Tawa1 last updated on 04/Jan/19

Commented by tanmay.chaudhury50@gmail.com last updated on 05/Jan/19
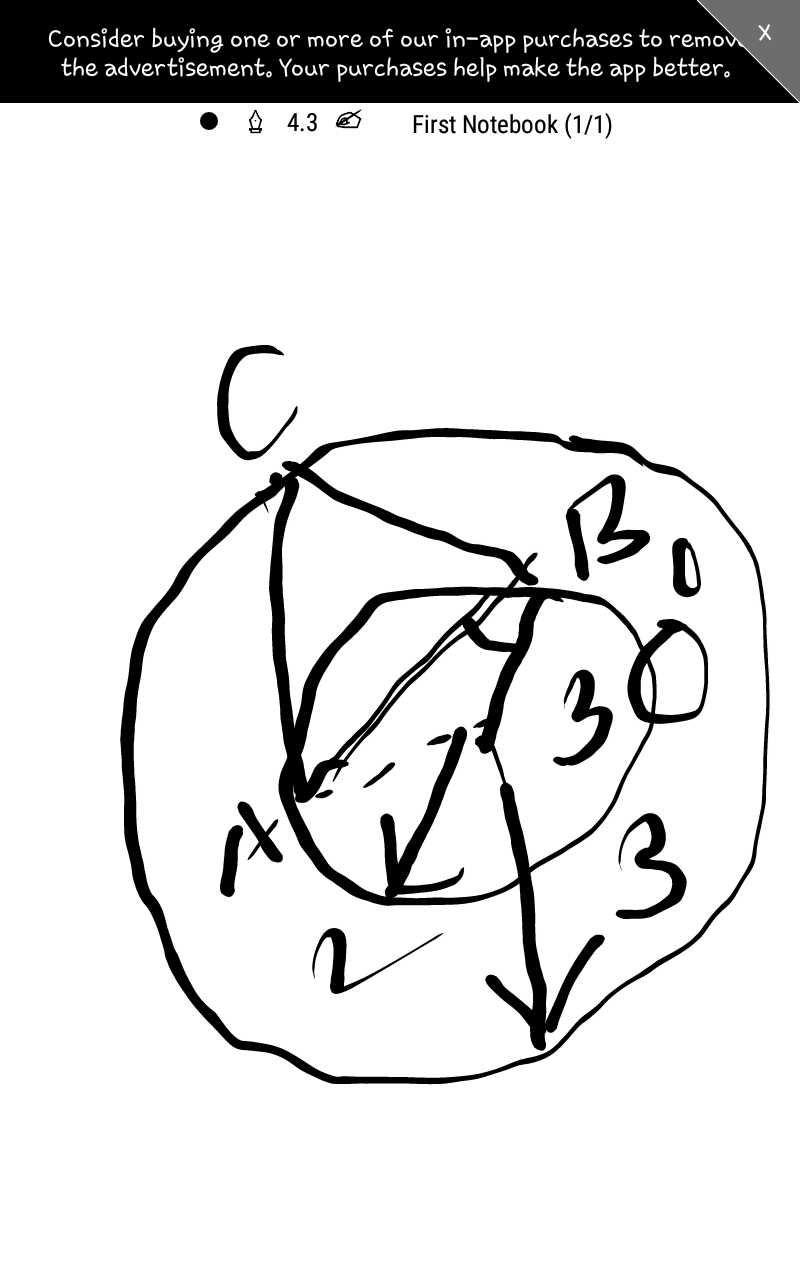
Commented by Tawa1 last updated on 05/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 05/Jan/19
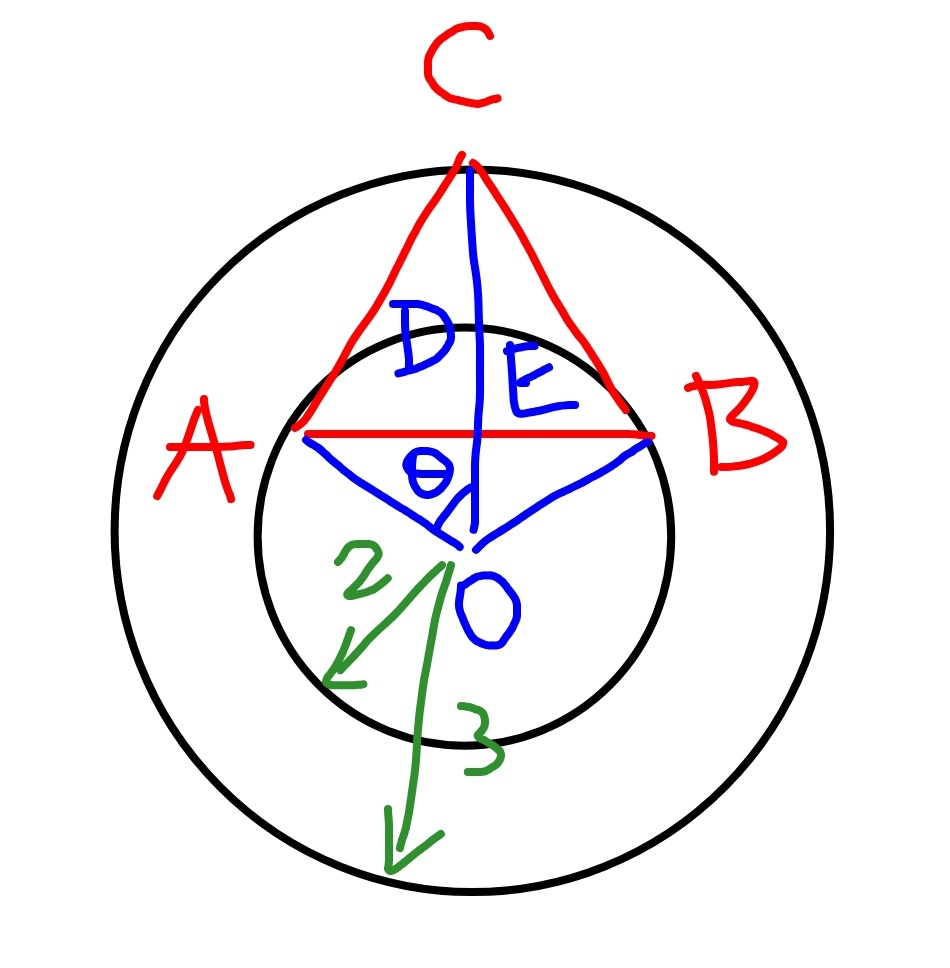
Commented by Tawa1 last updated on 05/Jan/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}.\: \\ $$
Commented by mr W last updated on 05/Jan/19

$${r}=\mathrm{2} \\ $$$${R}=\mathrm{3} \\ $$$${AB}={a} \\ $$$${DC}={R}−{r}=\mathrm{3}−\mathrm{2}=\mathrm{1} \\ $$$${AB}=\mathrm{2}{r}\:\mathrm{sin}\:\theta={a} \\ $$$${DE}={r}−{r}\:\mathrm{cos}\:\theta={r}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$${EC}={DE}+{DC}={r}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)+{R}−{r}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{a}\: \\ $$$$\Rightarrow{r}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)+{R}−{r}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\mathrm{2}{r}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)+\mathrm{1}=\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{sin}\:\theta+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\theta=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{cos}\:\frac{\pi}{\mathrm{6}}\:\mathrm{sin}\:\theta+\mathrm{sin}\:\frac{\pi}{\mathrm{6}}\mathrm{cos}\:\theta=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right)=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\theta+\frac{\pi}{\mathrm{6}}=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\:{or}\:\pi−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\theta=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}−\frac{\pi}{\mathrm{6}}\:\left(\approx\mathrm{18}.\mathrm{59}°\right)\:{or} \\ $$$$\Rightarrow\theta=\frac{\mathrm{5}\pi}{\mathrm{6}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\:\left(\approx\mathrm{101}.\mathrm{41}°\right) \\ $$$${i}.{e}.\:{two}\:{equilateral}\:{triangles}\:{are}\:{possible}. \\ $$$$ \\ $$$${a}=\mathrm{2}{r}\:\mathrm{sin}\:\theta=\mathrm{4}\:\mathrm{sin}\:\theta \\ $$$$\mathrm{sin}\:\theta=\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}−\frac{\pi}{\mathrm{6}}\right)=\frac{\mathrm{3}}{\mathrm{4}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}\sqrt{\mathrm{3}}−\sqrt{\mathrm{7}}}{\mathrm{8}} \\ $$$$\mathrm{sin}\:\theta=\mathrm{sin}\:\left(\frac{\mathrm{5}\pi}{\mathrm{6}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\right)=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\right)=\frac{\mathrm{3}}{\mathrm{4}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}\sqrt{\mathrm{3}}+\sqrt{\mathrm{7}}}{\mathrm{8}} \\ $$$$\Rightarrow{a}=\frac{\mathrm{3}\sqrt{\mathrm{3}}−\sqrt{\mathrm{7}}}{\mathrm{2}}\:\left(\approx\mathrm{1}.\mathrm{275}\right)\:{or} \\ $$$$\Rightarrow{a}=\frac{\mathrm{3}\sqrt{\mathrm{3}}+\sqrt{\mathrm{7}}}{\mathrm{2}}\:\left(\approx\mathrm{3}.\mathrm{921}\right) \\ $$$${product}\:{of}\:{possible}\:{side}\:{lengthes}\:{is} \\ $$$${P}=\frac{\mathrm{3}\sqrt{\mathrm{3}}−\sqrt{\mathrm{7}}}{\mathrm{2}}×\frac{\mathrm{3}\sqrt{\mathrm{3}}+\sqrt{\mathrm{7}}}{\mathrm{2}}=\frac{\mathrm{9}×\mathrm{3}−\mathrm{7}}{\mathrm{4}}=\mathrm{5} \\ $$$$ \\ $$$$\Rightarrow{the}\:{answer}\:{is}\:\mathrm{5}. \\ $$
Commented by mr W last updated on 05/Jan/19

$${alternative}\:{way}: \\ $$$${AB}={a} \\ $$$${OE}=\sqrt{{r}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$${CE}={R}−\sqrt{{r}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}} \\ $$$$\mathrm{3}−\sqrt{\mathrm{4}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}} \\ $$$$\sqrt{\mathrm{16}−{a}^{\mathrm{2}} }=\mathrm{6}−\sqrt{\mathrm{3}}{a} \\ $$$$\mathrm{16}−{a}^{\mathrm{2}} =\mathrm{36}−\mathrm{12}\sqrt{\mathrm{3}}{a}+\mathrm{3}{a}^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} −\mathrm{3}\sqrt{\mathrm{3}}{a}+\mathrm{5}=\mathrm{0} \\ $$$${there}\:{are}\:{two}\:{solutions}\:{for}\:{a}.\:{the} \\ $$$${sum}\:{of}\:{both}\:{solutions}\:{is}\:\mathrm{3}\sqrt{\mathrm{3}}\:{and}\:{the} \\ $$$${product}\:{of}\:{both}\:{solutions}\:{is}\:\mathrm{5}. \\ $$$$ \\ $$$$\Rightarrow{answer}\:{is}\:\mathrm{5}. \\ $$
