Question Number 52261 by mr W last updated on 05/Jan/19
Commented by mr W last updated on 05/Jan/19

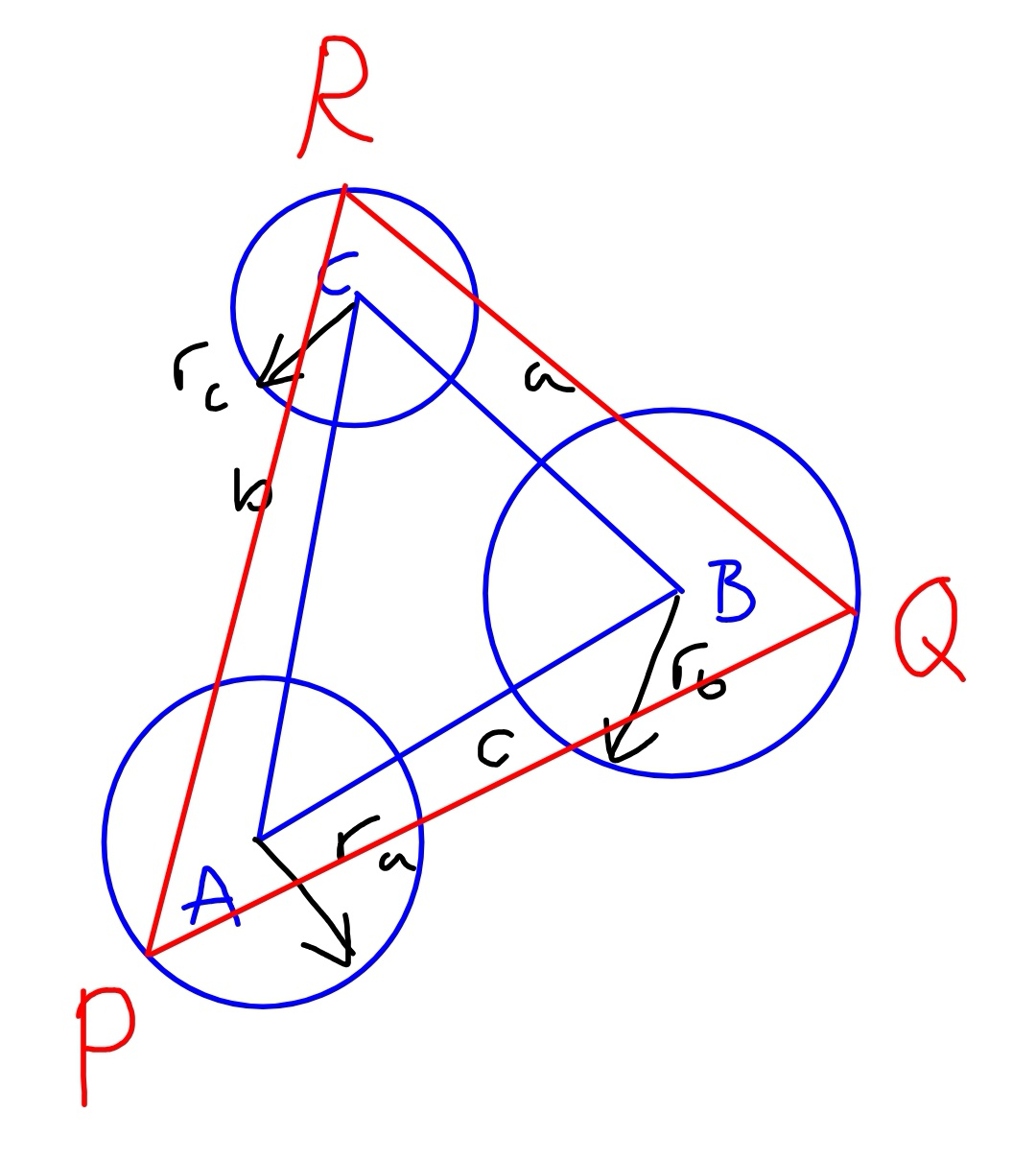
$${Three}\:{circles}\:{with}\:{radii}\:{r}_{{a}} ,{r}_{{b}} \:{and}\:{r}_{{c}} \\ $$$${have}\:{their}\:{centers}\:{at}\:{A},\:{B}\:{and}\:{C}\:{which} \\ $$$${have}\:{distances}\:{a},\:{b}\:{and}\:{c}\:{to}\:{each}\:{other}. \\ $$$${Find}\:{the}\:{maximum}\:{and}\:{minimum} \\ $$$${area}\:{of}\:{the}\:{triangle}\:{whose}\:{vertexes} \\ $$$${are}\:{on}\:{each}\:{of}\:{the}\:{circles}. \\ $$
Commented by behi83417@gmail.com last updated on 05/Jan/19
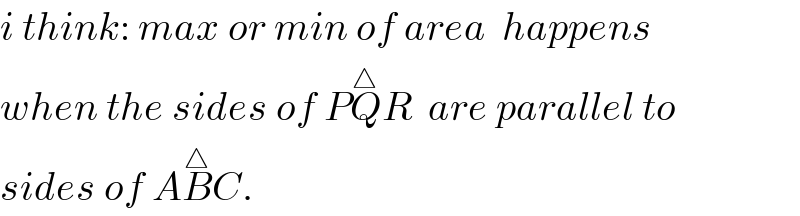
$${i}\:{think}:\:{max}\:{or}\:{min}\:{of}\:{area}\:\:{happens} \\ $$$${when}\:{the}\:{sides}\:{of}\:{P}\overset{\bigtriangleup} {{Q}R}\:\:{are}\:{parallel}\:{to} \\ $$$${sides}\:{of}\:{A}\overset{\bigtriangleup} {{B}C}. \\ $$
Commented by mr W last updated on 06/Jan/19

$${since}\:{the}\:{circles}\:{have}\:{different}\:{radii}, \\ $$$${it}\:{is}\:{not}\:{always}\:{possible}\:{to}\:{build}\:{a}\:{triangle} \\ $$$${PQR}\:{whose}\:{sides}\:{are}\:{parallel}\:{to}\:{the} \\ $$$${sides}\:{from}\:{triangle}\:{ABC}. \\ $$
Commented by ajfour last updated on 05/Jan/19
Commented by ajfour last updated on 05/Jan/19
$${shall}\:{attempt}\:{later},\:{Sir}. \\ $$
Commented by mr W last updated on 06/Jan/19

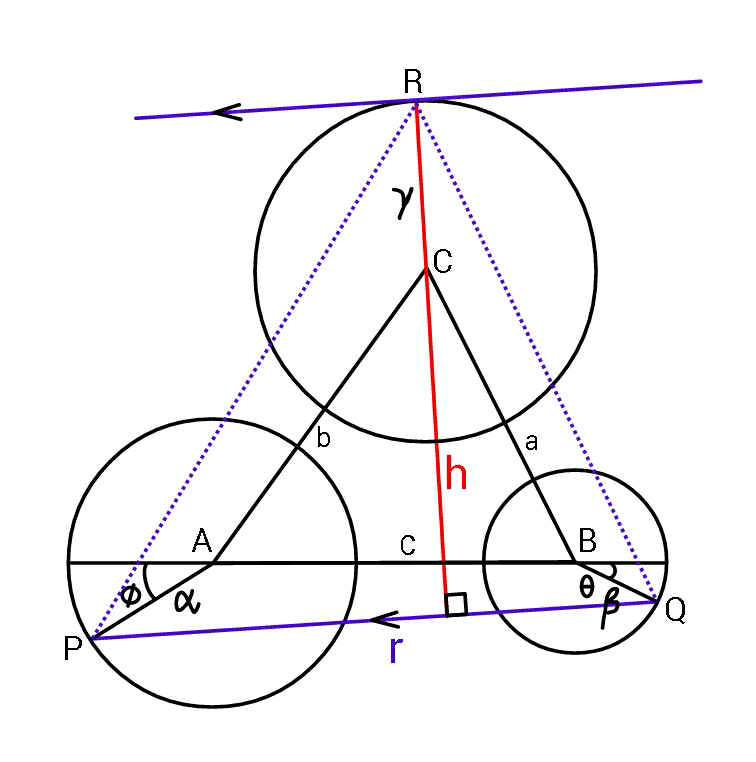
$${thank}\:{you}\:{sir}.\:{it}'{s}\:{correct}: \\ $$$${the}\:{maximum}\:\left({as}\:{well}\:{as}\:{the}\:{minimum}\right) \\ $$$${triangle}\:{PQR}\:{should}\:{be}\:{constructed} \\ $$$${in}\:{the}\:{way}\:{that}\:{the}\:{tangent}\:{at}\:{R}\:{is} \\ $$$${parallel}\:{to}\:{the}\:{side}\:{PQ}\:{and}\:{the}\:{tangent} \\ $$$${at}\:{P}\:{is}\:{parallel}\:{to}\:{the}\:{side}\:{QR}\:{and}\:{the} \\ $$$${tangent}\:{at}\:{Q}\:{is}\:{parallel}\:{to}\:{the}\:{side}\:{RP}. \\ $$$${i}.{e}.\:{CR}\bot{PQ},\:{AP}\bot{QR},\:{BQ}\bot{RP}. \\ $$
Commented by ajfour last updated on 06/Jan/19
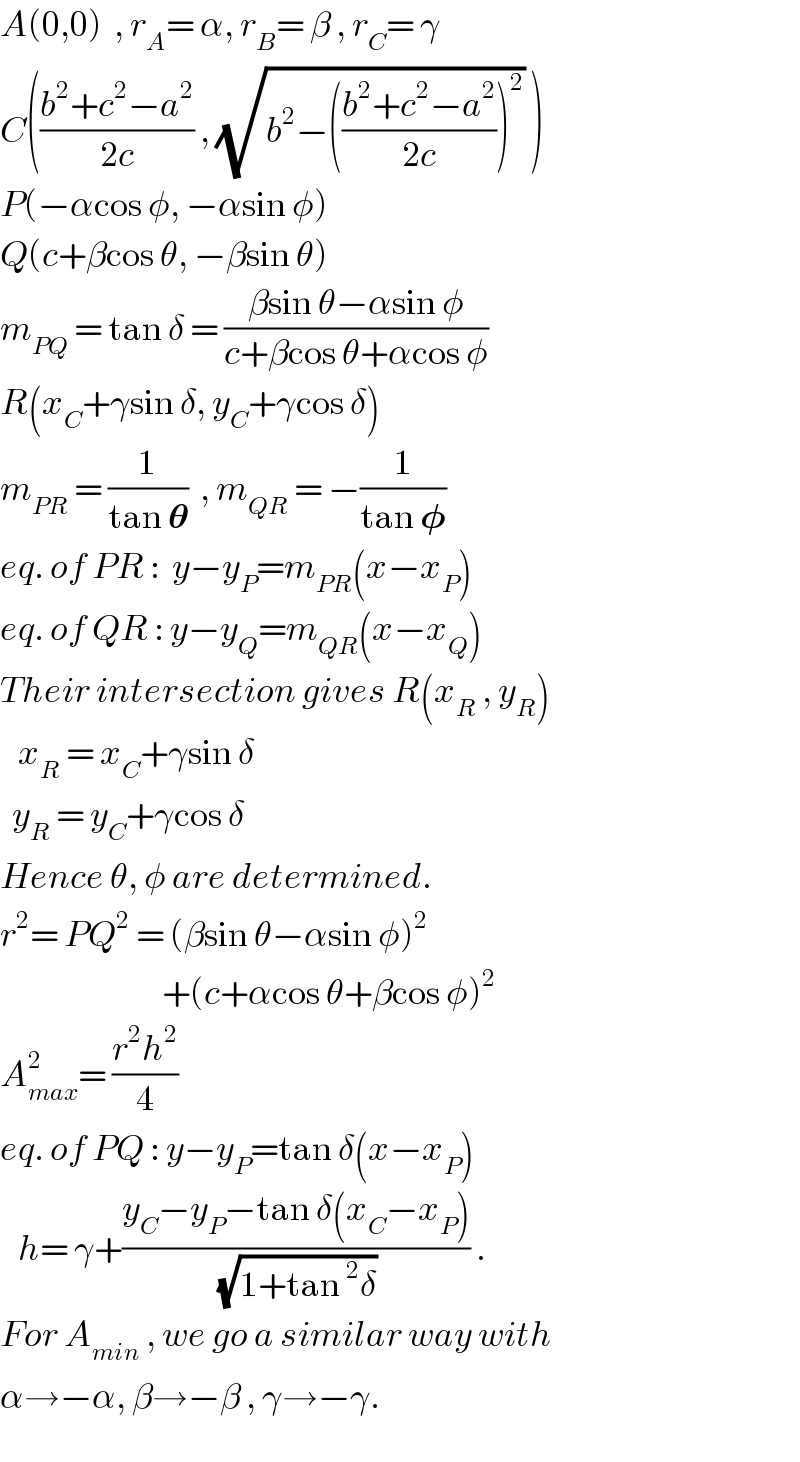
$${A}\left(\mathrm{0},\mathrm{0}\right)\:\:,\:{r}_{{A}} =\:\alpha,\:{r}_{{B}} =\:\beta\:,\:{r}_{{C}} =\:\gamma \\ $$$${C}\left(\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{c}}\:,\:\sqrt{{b}^{\mathrm{2}} −\left(\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{c}}\right)^{\mathrm{2}} }\:\right) \\ $$$${P}\left(−\alpha\mathrm{cos}\:\phi,\:−\alpha\mathrm{sin}\:\phi\right) \\ $$$${Q}\left({c}+\beta\mathrm{cos}\:\theta,\:−\beta\mathrm{sin}\:\theta\right) \\ $$$${m}_{{PQ}} \:=\:\mathrm{tan}\:\delta\:=\:\frac{\beta\mathrm{sin}\:\theta−\alpha\mathrm{sin}\:\phi}{{c}+\beta\mathrm{cos}\:\theta+\alpha\mathrm{cos}\:\phi} \\ $$$${R}\left({x}_{{C}} +\gamma\mathrm{sin}\:\delta,\:{y}_{{C}} +\gamma\mathrm{cos}\:\delta\right) \\ $$$${m}_{{PR}} \:=\:\frac{\mathrm{1}}{\mathrm{tan}\:\boldsymbol{\theta}}\:\:,\:{m}_{{QR}} \:=\:−\frac{\mathrm{1}}{\mathrm{tan}\:\boldsymbol{\phi}} \\ $$$${eq}.\:{of}\:{PR}\::\:\:{y}−{y}_{{P}} ={m}_{{PR}} \left({x}−{x}_{{P}} \right) \\ $$$${eq}.\:{of}\:{QR}\::\:{y}−{y}_{{Q}} ={m}_{{QR}} \left({x}−{x}_{{Q}} \right) \\ $$$${Their}\:{intersection}\:{gives}\:{R}\left({x}_{{R}} \:,\:{y}_{{R}} \right) \\ $$$$\:\:\:{x}_{{R}} \:=\:{x}_{{C}} +\gamma\mathrm{sin}\:\delta \\ $$$$\:\:{y}_{{R}} \:=\:{y}_{{C}} +\gamma\mathrm{cos}\:\delta \\ $$$${Hence}\:\theta,\:\phi\:{are}\:{determined}. \\ $$$${r}^{\mathrm{2}} =\:{PQ}^{\mathrm{2}} \:=\:\left(\beta\mathrm{sin}\:\theta−\alpha\mathrm{sin}\:\phi\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({c}+\alpha\mathrm{cos}\:\theta+\beta\mathrm{cos}\:\phi\right)^{\mathrm{2}} \\ $$$${A}_{{max}} ^{\mathrm{2}} =\:\frac{{r}^{\mathrm{2}} {h}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${eq}.\:{of}\:{PQ}\::\:{y}−{y}_{{P}} =\mathrm{tan}\:\delta\left({x}−{x}_{{P}} \right) \\ $$$$\:\:\:{h}=\:\gamma+\frac{{y}_{{C}} −{y}_{{P}} −\mathrm{tan}\:\delta\left({x}_{{C}} −{x}_{{P}} \right)}{\:\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \delta}}\:. \\ $$$${For}\:{A}_{{min}} \:,\:{we}\:{go}\:{a}\:{similar}\:{way}\:{with} \\ $$$$\alpha\rightarrow−\alpha,\:\beta\rightarrow−\beta\:,\:\gamma\rightarrow−\gamma. \\ $$
Commented by ajfour last updated on 06/Jan/19

$${Yes}\:{Sir},\:{thank}\:{you}.\:{Splendid}\:{question}! \\ $$
Commented by mr W last updated on 06/Jan/19
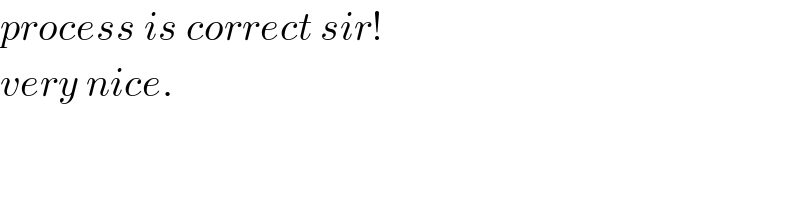
$${process}\:{is}\:{correct}\:{sir}! \\ $$$${very}\:{nice}. \\ $$
