Menu Close

1-2-3-4-S-2-4-6-8-10-2S-S-2S-1-3-5-7-2S-S-lim-x-n-n-1-2-lim-x-n-2-S-1-2-3-4-

Tinku Tara 0 Comments
Pin




Question Number 5157 by 1771727373 last updated on 24/Apr/16
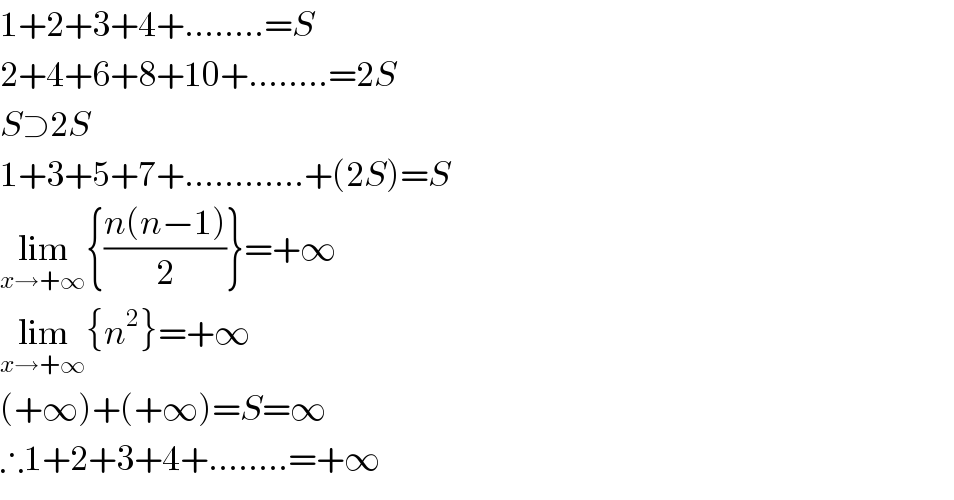
1+2+3+4+........=S 2+4+6+8+10+........=2S S⊃2S 1+3+5+7+............+(2S)=S lim_(x→+∞) {((n(n−1))/2)}=+∞ lim_(x→+∞) {n^2 }=+∞ (+∞)+(+∞)=S=∞ ∴1+2+3+4+........=+∞
$$\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+……..={S} \\ $$$$\mathrm{2}+\mathrm{4}+\mathrm{6}+\mathrm{8}+\mathrm{10}+……..=\mathrm{2}{S} \\ $$$${S}\supset\mathrm{2}{S} \\ $$$$\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}+…………+\left(\mathrm{2}{S}\right)={S} \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left\{\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}\right\}=+\infty \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left\{{n}^{\mathrm{2}} \right\}=+\infty \\ $$$$\left(+\infty\right)+\left(+\infty\right)={S}=\infty \\ $$$$\therefore\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+……..=+\infty \\ $$
Commented by FilupSmith last updated on 24/Apr/16
This is both correct and incorrect. When looking at S, it does diverge. But with analytical continuation, you can show that S=−(1/(12)) This sequence is also known as ζ(−1). I do not rememberthe proof, but I believe Yozzii may be able to show you
$$\mathrm{This}\:\mathrm{is}\:\mathrm{both}\:\mathrm{correct}\:\mathrm{and}\:\mathrm{incorrect}. \\ $$$$ \\ $$$$\mathrm{When}\:\mathrm{looking}\:\mathrm{at}\:{S},\:\mathrm{it}\:\mathrm{does}\:\mathrm{diverge}.\:\mathrm{But} \\ $$$$\mathrm{with}\:\mathrm{analytical}\:\mathrm{continuation},\:\mathrm{you}\:\mathrm{can} \\ $$$$\mathrm{show}\:\mathrm{that}\:{S}=−\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$\mathrm{This}\:\mathrm{sequence}\:\mathrm{is}\:\mathrm{also}\:\mathrm{known}\:\mathrm{as}\:\zeta\left(−\mathrm{1}\right). \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{do}\:\mathrm{not}\:\mathrm{rememberthe}\:\mathrm{proof},\:\mathrm{but}\:\mathrm{I}\:\mathrm{believe} \\ $$$$\mathrm{Yozzii}\:\mathrm{may}\:\mathrm{be}\:\mathrm{able}\:\mathrm{to}\:\mathrm{show}\:\mathrm{you} \\ $$
Commented by Yozzii last updated on 25/Apr/16
A test for divergence of a series given by Σ_(i=1) ^∞ f(i) is lim_(n→∞) f(n)≠0. In this question f(n)=n ⇒lim_(n→∞) f(n)=lim_(n→∞) n=∞≠0. ∴ 1+2+3+... is divergent. Since also 1+2+3+...+n=((n(n+1))/2) and ((n(n+1))/2) is an increasing function for all n≥1, then lim_(n→∞) ((n(n+1))/2) does not exist and is arbitrarily large as n→∞.
$${A}\:{test}\:{for}\:{divergence}\:{of}\:{a}\:{series}\:{given} \\ $$$${by}\:\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{f}\left({i}\right)\:{is}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{f}\left({n}\right)\neq\mathrm{0}. \\ $$$${In}\:{this}\:{question}\:{f}\left({n}\right)={n} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}{f}\left({n}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}{n}=\infty\neq\mathrm{0}. \\ $$$$\therefore\:\mathrm{1}+\mathrm{2}+\mathrm{3}+…\:{is}\:{divergent}. \\ $$$${Since}\:{also}\:\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{n}=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$${and}\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:{is}\:{an}\:{increasing}\:{function} \\ $$$${for}\:{all}\:{n}\geqslant\mathrm{1},\:{then}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:{does} \\ $$$${not}\:{exist}\:{and}\:{is}\:{arbitrarily}\:{large} \\ $$$${as}\:{n}\rightarrow\infty. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *