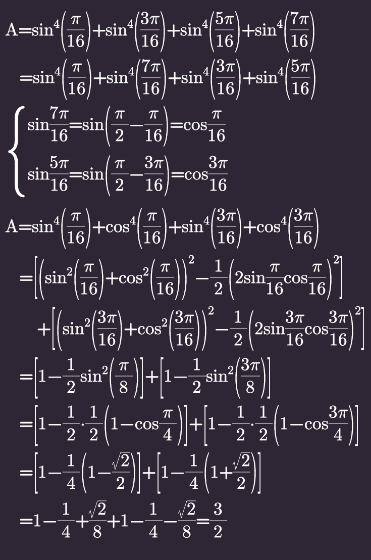Menu Close

sin-4-pi-16-sin-4-3pi-16-sin-4-5pi-16-sin-4-7pi-16-

Tinku Tara
Pin




Question Number 131492 by Ar Brandon last updated on 05/Feb/21
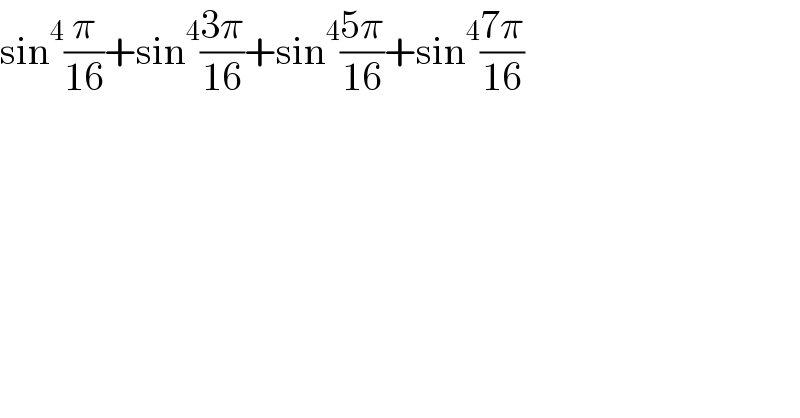
sin^4 (π/(16))+sin^4 ((3π)/(16))+sin^4 ((5π)/(16))+sin^4 ((7π)/(16))
$$\mathrm{sin}^{\mathrm{4}} \frac{\pi}{\mathrm{16}}+\mathrm{sin}^{\mathrm{4}} \frac{\mathrm{3}\pi}{\mathrm{16}}+\mathrm{sin}^{\mathrm{4}} \frac{\mathrm{5}\pi}{\mathrm{16}}+\mathrm{sin}^{\mathrm{4}} \frac{\mathrm{7}\pi}{\mathrm{16}} \\ $$
Answered by Dwaipayan Shikari last updated on 05/Feb/21
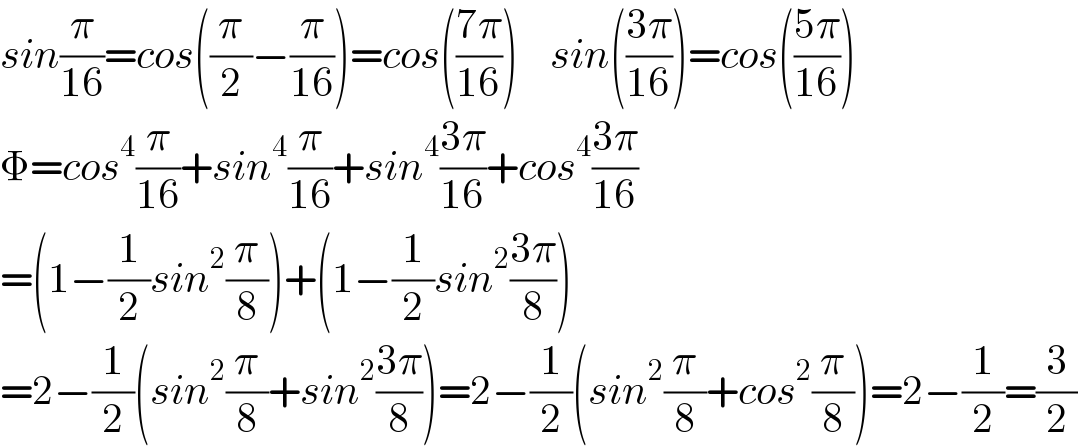
sin(π/(16))=cos((π/2)−(π/(16)))=cos(((7π)/(16))) sin(((3π)/(16)))=cos(((5π)/(16))) Φ=cos^4 (π/(16))+sin^4 (π/(16))+sin^4 ((3π)/(16))+cos^4 ((3π)/(16)) =(1−(1/2)sin^2 (π/8))+(1−(1/2)sin^2 ((3π)/8)) =2−(1/2)(sin^2 (π/8)+sin^2 ((3π)/8))=2−(1/2)(sin^2 (π/8)+cos^2 (π/8))=2−(1/2)=(3/2)
$${sin}\frac{\pi}{\mathrm{16}}={cos}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{16}}\right)={cos}\left(\frac{\mathrm{7}\pi}{\mathrm{16}}\right)\:\:\:\:{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{16}}\right)={cos}\left(\frac{\mathrm{5}\pi}{\mathrm{16}}\right) \\ $$$$\Phi={cos}^{\mathrm{4}} \frac{\pi}{\mathrm{16}}+{sin}^{\mathrm{4}} \frac{\pi}{\mathrm{16}}+{sin}^{\mathrm{4}} \frac{\mathrm{3}\pi}{\mathrm{16}}+{cos}^{\mathrm{4}} \frac{\mathrm{3}\pi}{\mathrm{16}} \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}\right)+\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$$$=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\left({sin}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}+{sin}^{\mathrm{2}} \frac{\mathrm{3}\pi}{\mathrm{8}}\right)=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\left({sin}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}+{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}\right)=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 05/Feb/21
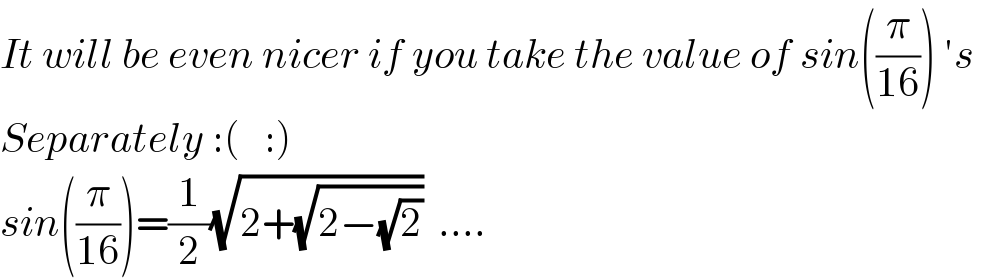
It will be even nicer if you take the value of sin((π/(16))) ′s Separately :( :) sin((π/(16)))=(1/2)(√(2+(√(2−(√2))))) ....
$${It}\:{will}\:{be}\:{even}\:{nicer}\:{if}\:{you}\:{take}\:{the}\:{value}\:{of}\:{sin}\left(\frac{\pi}{\mathrm{16}}\right)\:'{s}\: \\ $$$${Separately}\::\left(\:\:\::\right) \\ $$$${sin}\left(\frac{\pi}{\mathrm{16}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}\:\:…. \\ $$
Commented by Ar Brandon last updated on 05/Feb/21
����
Answered by Ar Brandon last updated on 05/Feb/21

Pin