Question Number 70720 by oyemi kemewari last updated on 07/Oct/19
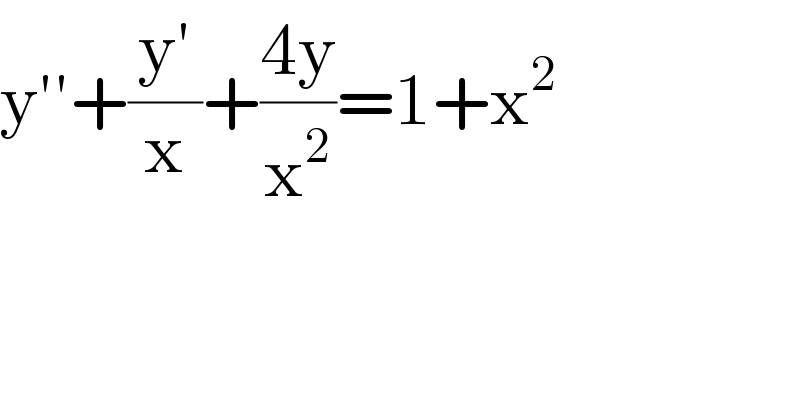
$$\mathrm{y}''+\frac{\mathrm{y}'}{\mathrm{x}}+\frac{\mathrm{4y}}{\mathrm{x}^{\mathrm{2}} }=\mathrm{1}+\mathrm{x}^{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 07/Oct/19

$$\mathcal{T}{hank}\:{you}! \\ $$
Commented by Rasheed.Sindhi last updated on 07/Oct/19
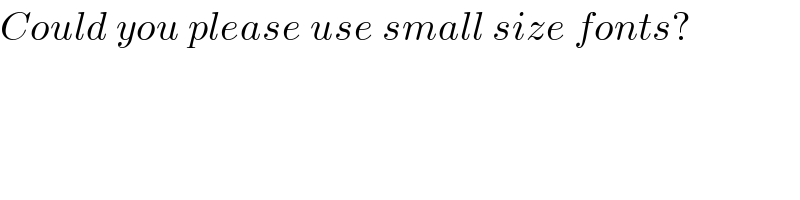
$${Could}\:{you}\:{please}\:{use}\:{small}\:{size}\:{fonts}? \\ $$
Commented by oyemi kemewari last updated on 07/Oct/19
ok sir
Commented by mind is power last updated on 07/Oct/19
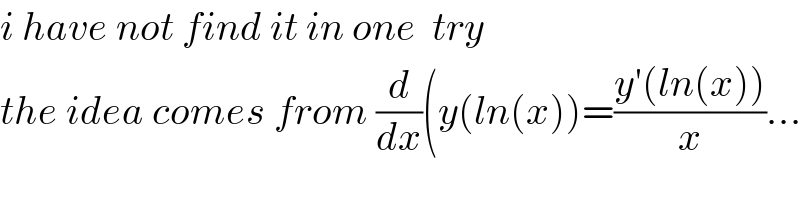
$${i}\:{have}\:{not}\:{find}\:{it}\:{in}\:{one}\:\:{try}\: \\ $$$${the}\:{idea}\:{comes}\:{from}\:\frac{{d}}{{dx}}\left({y}\left({ln}\left({x}\right)\right)=\frac{{y}'\left({ln}\left({x}\right)\right)}{{x}}…\right. \\ $$
Answered by mind is power last updated on 07/Oct/19
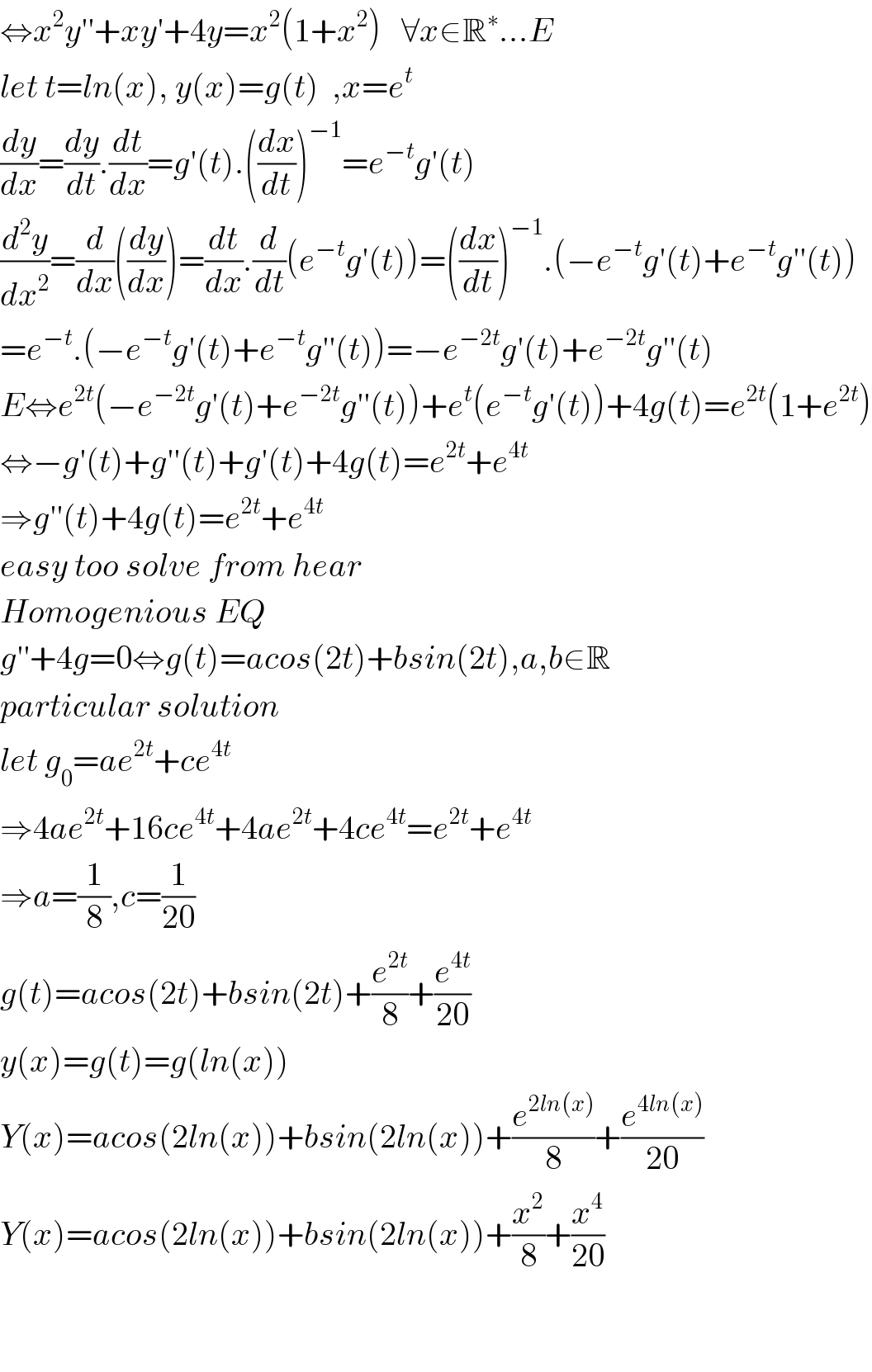
$$\Leftrightarrow{x}^{\mathrm{2}} {y}''+{xy}'+\mathrm{4}{y}={x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:\:\:\forall{x}\in\mathbb{R}^{\ast} …{E} \\ $$$${let}\:{t}={ln}\left({x}\right),\:{y}\left({x}\right)={g}\left({t}\right)\:\:,{x}={e}^{{t}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{dt}}.\frac{{dt}}{{dx}}={g}'\left({t}\right).\left(\frac{{dx}}{{dt}}\right)^{−\mathrm{1}} ={e}^{−{t}} {g}'\left({t}\right) \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{d}}{{dx}}\left(\frac{{dy}}{{dx}}\right)=\frac{{dt}}{{dx}}.\frac{{d}}{{dt}}\left({e}^{−{t}} {g}'\left({t}\right)\right)=\left(\frac{{dx}}{{dt}}\right)^{−\mathrm{1}} .\left(−{e}^{−{t}} {g}'\left({t}\right)+{e}^{−{t}} {g}''\left({t}\right)\right) \\ $$$$={e}^{−{t}} .\left(−{e}^{−{t}} {g}'\left({t}\right)+{e}^{−{t}} {g}''\left({t}\right)\right)=−{e}^{−\mathrm{2}{t}} {g}'\left({t}\right)+{e}^{−\mathrm{2}{t}} {g}''\left({t}\right) \\ $$$${E}\Leftrightarrow{e}^{\mathrm{2}{t}} \left(−{e}^{−\mathrm{2}{t}} {g}'\left({t}\right)+{e}^{−\mathrm{2}{t}} {g}''\left({t}\right)\right)+{e}^{{t}} \left({e}^{−{t}} {g}'\left({t}\right)\right)+\mathrm{4}{g}\left({t}\right)={e}^{\mathrm{2}{t}} \left(\mathrm{1}+{e}^{\mathrm{2}{t}} \right) \\ $$$$\Leftrightarrow−{g}'\left({t}\right)+{g}''\left({t}\right)+{g}'\left({t}\right)+\mathrm{4}{g}\left({t}\right)={e}^{\mathrm{2}{t}} +{e}^{\mathrm{4}{t}} \\ $$$$\Rightarrow{g}''\left({t}\right)+\mathrm{4}{g}\left({t}\right)={e}^{\mathrm{2}{t}} +{e}^{\mathrm{4}{t}} \\ $$$${easy}\:{too}\:{solve}\:{from}\:{hear} \\ $$$${Homogenious}\:{EQ} \\ $$$${g}''+\mathrm{4}{g}=\mathrm{0}\Leftrightarrow{g}\left({t}\right)={acos}\left(\mathrm{2}{t}\right)+{bsin}\left(\mathrm{2}{t}\right),{a},{b}\in\mathbb{R} \\ $$$${particular}\:{solution}\: \\ $$$${let}\:{g}_{\mathrm{0}} ={ae}^{\mathrm{2}{t}} +{ce}^{\mathrm{4}{t}} \\ $$$$\Rightarrow\mathrm{4}{ae}^{\mathrm{2}{t}} +\mathrm{16}{ce}^{\mathrm{4}{t}} +\mathrm{4}{ae}^{\mathrm{2}{t}} +\mathrm{4}{ce}^{\mathrm{4}{t}} ={e}^{\mathrm{2}{t}} +{e}^{\mathrm{4}{t}} \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}}{\mathrm{8}},{c}=\frac{\mathrm{1}}{\mathrm{20}} \\ $$$${g}\left({t}\right)={acos}\left(\mathrm{2}{t}\right)+{bsin}\left(\mathrm{2}{t}\right)+\frac{{e}^{\mathrm{2}{t}} }{\mathrm{8}}+\frac{{e}^{\mathrm{4}{t}} }{\mathrm{20}} \\ $$$${y}\left({x}\right)={g}\left({t}\right)={g}\left({ln}\left({x}\right)\right) \\ $$$${Y}\left({x}\right)={acos}\left(\mathrm{2}{ln}\left({x}\right)\right)+{bsin}\left(\mathrm{2}{ln}\left({x}\right)\right)+\frac{{e}^{\mathrm{2}{ln}\left({x}\right)} }{\mathrm{8}}+\frac{{e}^{\mathrm{4}{ln}\left({x}\right)} }{\mathrm{20}} \\ $$$${Y}\left({x}\right)={acos}\left(\mathrm{2}{ln}\left({x}\right)\right)+{bsin}\left(\mathrm{2}{ln}\left({x}\right)\right)+\frac{{x}^{\mathrm{2}} }{\mathrm{8}}+\frac{{x}^{\mathrm{4}} }{\mathrm{20}} \\ $$$$ \\ $$$$ \\ $$
Commented by oyemi kemewari last updated on 07/Oct/19
thank you sir
Commented by mind is power last updated on 07/Oct/19

$${y}'{re}\:{Welcom} \\ $$
Answered by Joel122 last updated on 08/Oct/19
![y′′ + ((1/x))y′ + ((4/x^2 ))y = 1 + x^2 x^2 y′′ + xy′ + 4y = x^2 + x^4 ... (i) • Homogeneous solution x^2 y′′ + xy′ + 4y = 0 → Euler−Cauchy eq. Let y(x) = x^m be the solution. Then, x^m [(m^2 − m) + m + 4] = 0 ⇒ m^2 + 4 = 0 ⇒ m_1 = 2i, m_2 = −2i ⇒ y_h (x) = C_1 x^(2i) + C_2 x^(−2i) = α cos (ln x^2 ) + β sin (ln x^2 ) • Particular solution Using method of undetermined parameter, we have y_p (x) = Ax^4 + Bx^3 + Cx^2 + Dx + E y_p ^′ (x) = 4Ax^3 + 3Bx^2 + 2Cx + D y_p ^(′′) (x) = 12Ax^2 + 6Bx + 2C Plugging these equations to (i) x^2 [12Ax^2 + 6Bx + 2C] + x[4Ax^3 + 3Bx^2 + 2Cx + D] + 4[Ax^4 + Bx^3 + Cx^2 + Dx + E] = x^2 + x^4 ⇒ 20Ax^4 + 13Bx^3 + 8Cx^2 + 5Dx + 4E = x^4 + x^2 By comparing the coefficients, we have A = (1/(20)), B = 0, C = (1/8), D = 0, E = 0 ⇒ y_p (x) = (x^4 /(20)) + (x^2 /8) ∴ y(x) = y_h (x) + y_p (x)](https://www.tinkutara.com/question/Q70745.png)
$${y}''\:+\:\left(\frac{\mathrm{1}}{{x}}\right){y}'\:+\:\left(\frac{\mathrm{4}}{{x}^{\mathrm{2}} }\right){y}\:=\:\mathrm{1}\:+\:{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {y}''\:+\:{xy}'\:+\:\mathrm{4}{y}\:=\:{x}^{\mathrm{2}} \:+\:{x}^{\mathrm{4}} \:\:\:\:\:\:\:\:…\:\left({i}\right) \\ $$$$ \\ $$$$\bullet\:\mathrm{Homogeneous}\:\mathrm{solution} \\ $$$${x}^{\mathrm{2}} {y}''\:+\:{xy}'\:+\:\mathrm{4}{y}\:=\:\mathrm{0}\:\:\rightarrow\:\:\mathrm{Euler}−\mathrm{Cauchy}\:\mathrm{eq}. \\ $$$$\mathrm{Let}\:{y}\left({x}\right)\:=\:{x}^{{m}} \:\mathrm{be}\:\mathrm{the}\:\mathrm{solution}.\:\mathrm{Then}, \\ $$$${x}^{{m}} \left[\left({m}^{\mathrm{2}} \:−\:{m}\right)\:+\:{m}\:+\:\mathrm{4}\right]\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{m}^{\mathrm{2}} \:+\:\mathrm{4}\:=\:\mathrm{0}\:\Rightarrow\:{m}_{\mathrm{1}} \:=\:\mathrm{2}{i},\:{m}_{\mathrm{2}} \:=\:−\mathrm{2}{i} \\ $$$$\Rightarrow\:{y}_{{h}} \left({x}\right)\:=\:{C}_{\mathrm{1}} {x}^{\mathrm{2}{i}} \:+\:{C}_{\mathrm{2}} {x}^{−\mathrm{2}{i}} \:=\:\alpha\:\mathrm{cos}\:\left(\mathrm{ln}\:{x}^{\mathrm{2}} \right)\:+\:\beta\:\mathrm{sin}\:\left(\mathrm{ln}\:{x}^{\mathrm{2}} \right)\: \\ $$$$ \\ $$$$\bullet\:\mathrm{Particular}\:\mathrm{solution} \\ $$$$\mathrm{Using}\:\mathrm{method}\:\mathrm{of}\:\mathrm{undetermined}\:\mathrm{parameter},\:\mathrm{we}\:\mathrm{have} \\ $$$${y}_{{p}} \left({x}\right)\:=\:{Ax}^{\mathrm{4}} \:+\:{Bx}^{\mathrm{3}} \:+\:{Cx}^{\mathrm{2}} \:+\:{Dx}\:+\:{E} \\ $$$${y}_{{p}} ^{'} \left({x}\right)\:=\:\mathrm{4}{Ax}^{\mathrm{3}} \:+\:\mathrm{3}{Bx}^{\mathrm{2}} \:+\:\mathrm{2}{Cx}\:+\:{D} \\ $$$${y}_{{p}} ^{''} \left({x}\right)\:=\:\mathrm{12}{Ax}^{\mathrm{2}} \:+\:\mathrm{6}{Bx}\:+\:\mathrm{2}{C} \\ $$$$\mathrm{Plugging}\:\mathrm{these}\:\mathrm{equations}\:\mathrm{to}\:\left({i}\right) \\ $$$${x}^{\mathrm{2}} \left[\mathrm{12}{Ax}^{\mathrm{2}} \:+\:\mathrm{6}{Bx}\:+\:\mathrm{2}{C}\right]\:+\:{x}\left[\mathrm{4}{Ax}^{\mathrm{3}} \:+\:\mathrm{3}{Bx}^{\mathrm{2}} \:+\:\mathrm{2}{Cx}\:+\:{D}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\mathrm{4}\left[{Ax}^{\mathrm{4}} \:+\:{Bx}^{\mathrm{3}} \:+\:{Cx}^{\mathrm{2}} \:+\:{Dx}\:+\:{E}\right]\:=\:{x}^{\mathrm{2}} \:+\:{x}^{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{20}{Ax}^{\mathrm{4}} \:+\:\mathrm{13}{Bx}^{\mathrm{3}} \:+\:\mathrm{8}{Cx}^{\mathrm{2}} \:+\:\mathrm{5}{Dx}\:+\:\mathrm{4}{E}\:=\:{x}^{\mathrm{4}} \:+\:{x}^{\mathrm{2}} \\ $$$$\mathrm{By}\:\mathrm{comparing}\:\mathrm{the}\:\mathrm{coefficients},\:\mathrm{we}\:\mathrm{have} \\ $$$${A}\:=\:\frac{\mathrm{1}}{\mathrm{20}},\:{B}\:=\:\mathrm{0},\:{C}\:=\:\frac{\mathrm{1}}{\mathrm{8}},\:{D}\:=\:\mathrm{0},\:{E}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{y}_{{p}} \left({x}\right)\:=\:\frac{{x}^{\mathrm{4}} }{\mathrm{20}}\:+\:\frac{{x}^{\mathrm{2}} }{\mathrm{8}} \\ $$$$ \\ $$$$\therefore\:{y}\left({x}\right)\:=\:{y}_{{h}} \left({x}\right)\:+\:{y}_{{p}} \left({x}\right) \\ $$
